1. 引言
热力学理论在一个多世纪之前被提出,已经揭示了许多不同物理现象的基本性质 [1] [2]。这个理论的特点是在不考虑微观成分基本性质的情况下有效地描述宏观系统的热力学行为。总的来说,热力学就是专注于研究系统的总能量是如何变化的,以及外界对其变化的影响 [3] [4] [5]。首先一个核心问题是第一定律,它表述了能量守恒:“在一个不能与周围介质交换任何物质的系统中,功和热是能量传递的唯一两种形式。”功是能量的传递,它是由系统的广义坐标的变化所引起的,如体积,电极化和磁化的变化 [4]。另一方面,热被定义为系统与环境之间伴随熵传递的能量传输 [6] [7]。
热力学定律除了惊人的普适性之外,其另一个显著特点是,它仅用很少的物理量,比如:功,热和温度,完全描述了无数个不同的过程。原因是这些量是系统组成部分的平均集体行为的产物。然而,当我们处理具有少量组成部分的系统时,由于分子的不规则运动,这些热力学量的涨落变得相关,这就需要随机热力学来解释这些概率相关的量。以类似的方式,如果我们处理更小的系统,再加上热涨落,量子效应就会变得突出,这就对涉及的物理量增加了很多的不可预测性 [8]。针对这些情况,量子热力学产生了研究量子热力学定律的想法。为保持定理原始的简单性 [9] [10] [11],揭示量子现象(如相干 [12] 和纠缠 [13])对这些定律的实际影响至关重要 [14] [15] [16]。
本文从功和热的经典定义出发研究热力学第一定律在量子领域的推广。然而我们发现,当仅考虑量子功和热时,得到的结果与第一定律的经典形式不一致。我们通过研究量子变换中发生的相干动力学对能量贡献来解决这个问题,这是一个在经典热力学不存在的因素。我们的发现是根据原子自发发射的情况,在两能级原子系统的框架中讨论的。实际上,我们的研究是将文献 [4] 的例证做了一般性的推广。
2. 基本原理(理论模型)
本文研究中使用了量子操作描述的Kraus算符和表示 [17],在研究这个问题之前,为了讨论的完整性,我们简要回顾一下Kraus算符和量子热力学第一定律的相关知识。
2.1. Kraus算符及其表示
给定一个初始量子比特
,在外部环境下它的演化可以用Kraus算符作用之和来表示 [18]:
(1)
其中
是与单个量子比特退相干过程相关的Kraus算符,满足
(2)
这里
为单位算符。
2.2. 量子热力学第一定律
将热力学推广到量子体系面临着从热和功的正确定义到明确相干作用的挑战。如何定义功和热在量子热力学中仍然是一个有争议的话题,因此在量子体系中有必要重新审视这些历史悠久的概念。
考虑一个量子系统S,其密度矩阵
在哈密顿
下演化,并与外部环境耦合。系统的内能可以表示为
[19],一种常见的做法是基于总能量期望值的变化:
,将第一项(哈密顿量的变化)定义为功
,将第二项(状态变化)定义为热
。上述公式解释为热力学第一定律的微分形式。状态的变化可能与熵的变化有关,即热。但是,一般认为这样定义的量子热并不完全等同于经典热。由于相干性在量子体系中起着基础和独特的作用,必须同时考虑能量和相干的性质。因此,在量子热力学中,热力学第一定律可以被重新定义为 [4]:
(3)
这意味着量子相干就像功和热一样,是系统与环境之间能量交换的一种形式 [20]。这个关系提供了热力学第一定律的量子版本,类似于经典热力学
,其中
是外部环境对系统做的功的量,
是在一个无穷小的过程中向系统传递的热量。在这里,我们应该注意到C没有W和Q的经典类比。与经典定义不同,功和热不再是绝对量,而是像量子相干那样依赖于所选择的测量基 [21]。如果给定
和
,这些量原则上可以计算出来。它们在有限量子过程中的时间依赖性可以通过直接积分来计算。系统内能变化的表达式可以表示为 [4]
(4)
其中
。
是密度算符
的本征态,
是
的本征值,即
。在这里哈密顿量表示为
(5)
式中
和
分别是第n个能量本征值和本征态。有限量子过程中的功、热和量子相干也可以通过直接积分分别计算 [4]:
(6)
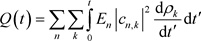 (7)
(7)
(8)
它们分别是功、热和相干动力学对能量的贡献。可以看到
、
和
取决于
。在量子过程中,只有当密度算符的基矢量
相对于哈密顿量的基矢量
的方向发生变化时,这些量才会变化。
3. 相干性对量子热力学的影响
我们现在考虑光子的自发发射问题,假设工作物质是一个两能级原子系统,其基态和激发态是
和
,能量分别为
和
,系统哈密顿量为
。下面考虑这个原子在一般振幅阻尼通道下的行为。这个通道的Kraus算符为:
(9)
其中
,
为单位时间内衰减事件的概率。由式(1)和(9)我们得到演化密度矩阵为
(10)
为了计算方便且不失一般性,我们取
,则上式可以简化为
(11)
由于能量本征值是常数(
),显然有,
。为了研究量子热力学第一定律,我们只需计算计算
、
和
,为此我们计算
得到其本征值为
(12)
(13)
对应的本征态为
(14)
(15)
其中,
,
,
,
。
下面假设原子的初态为
,我们计算得到原子与环境之间的热量交换为
(16)
其中,
相干的时间演化为
(17)
其中,
具体地,并不失一般性,我们取
,
,
,并令
,则
,
,
,
,由此可以得到
(18)
(19)
(20)
上述结果被画在图1中。从图中可以看到,热首先释放,然后被原子吸收,这是熵振荡的反射,这一过程还导致原子相干性的最大提取,这对内能的降低有显著贡献。因此,在系统达到稳定状态之前,会有信息流,从系统流向环境,正如我们看到的这种行为在图1所示的热力学量中表示出来。更重要的是,我们看到数值结果满足关系式(3),充分表明了相干在其中所起的作用。
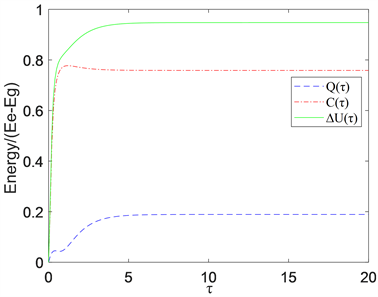
Figure 1. The first law of atomic spontaneous emission process, heat and coherent dynamics are equal to the change of internal energy, where the parameter is θ = 30˚
图1. 原子自发辐射过程的第一定律,热和相干动力学产生的能量等于内能的变化,其中参数θ = 30˚
为了进一步验证我们的结果,考虑取
时,则
,
,
,
,由此热量,相干以及内能分别为
(21)
(22)
(23)
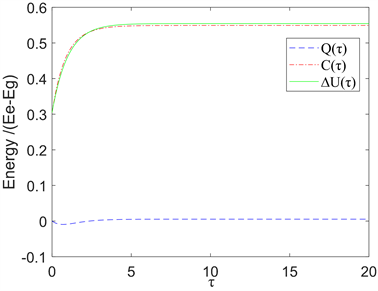
Figure 2. According to the first law of atomic spontaneous emission process, the energy generated by heat and coherent dynamics is equal to the change of internal energy. Blue represents thermal energy, parameter is θ = 60˚
图2. 原子自发辐射过程的第一定律,热和相干动力学产生的能量等于内能的变化,其中参数θ = 60˚
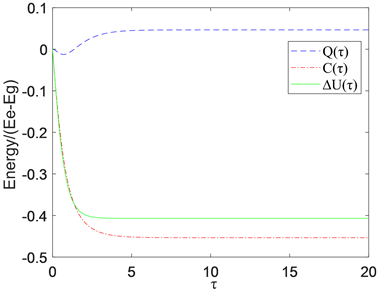
Figure 3. First-law description of the nonunitaryspontaneous emission process. Both and dynamics of coherence contribute to the change in the internal energy,
. Where the parameter is θ = 45˚
图3. 非均匀自发辐射的第一定律过程的描述,热和相干动力学都对内能的变化有贡献,
。其中θ = 45˚
我们画出上述数值结果,如图2所示。结果同样满足关系式(3),与图1比较发现,角度为30˚时相干产生的最大能比角度为60˚时更大且热能的最大值也有同样的变化趋势。因此,改变角度也就是改变系统的初始态,对系统的输出效率也会产生较大的变化,角度越小,相干动力学产生的最大能量越大。作为比较,我们还考虑了θ = 45˚时的情况,结果如图3所示,与文献 [4] 给出的结果一致。
4. 结论
本文利用经典热力学的功和热的概念,给出了量子体系中对应物理量。有了这些定义并运用数值模拟方法研究它们对热力学第一定律的作用,我们证明量子相干在内能变化中所起的作用是一个与功和热无关的源作用。具体地,我们通过研究原子自发辐射的过程,对原子在广义振幅阻尼通道中的行为进行了热力学描述,定量论证了功、热和相干动力学在第一定律中的贡献,发现了量子相干在热力学中的奇特行为:角度为30˚时,相干产生的最大能量可以达到0.78,角度为60˚时,相干产生的最大能量为0.55;我们相信,我们的结果对进一步完善量子热力学第一定律具有重要意义。
NOTES
*通讯作者。