1. 引言
质量、动能和作用力是反映物体在时空中存在的物理量,这些物理量的产生及其变化与时空有着密切的内在联系。
牛顿三大运动定律奠定了经典力学的基础,其中牛顿第二定律明确了力是物体运动状态发生改变的根本原因,通过公式F = ma,将力和质量联系起来,体现了力和质量的瞬间作用效应。与牛顿第二定律
密切相关的动能公式
又将动能和质量联系起来 [1]。
爱因斯坦相对论研究了质量、能量与时空的相对性关系,推导出质能公式E = mc2,说明质量与能量具有相同的本质 [2]。
随着量子力学、量子场论等量子理论的发展,物理学进入到微观粒子时代。经典物理描述的质量、动能和作用力更适合研究宏观物体,对微观粒子的研究存在很大的局限性 [3]。随着对微观粒子研究的不断深入,有必要将质量、动能和作用力等物理概念进行新的诠释,以便揭示出质量和作用力的真正本质以及它们与时空的内在关系,形成即适合宏观物体,又适合微观粒子的新的物理学方法和理论。
由经典力学推导出的质量、动能和作用力关于时空的二阶偏微分方程,
,揭示了作
用力和质量的本质以及质量和能量相互转发的时空原理,反映了质量、动能和作用力之间的内在关系,以及它们在时空中的瞬时效应。
2. 质量、动能与作用力关于时空的二阶偏微分方程
某惯性参照系中,给质量为m的静止物体A施加恒力F,作用力的方向通过A的质心,物体A可作为质点考虑。物体在F的作用下将以加速度a做匀加速直线运动。当物体的速度v远小于光速c时,忽略相对论效应,m、F、a为不变量,v、t (时间)、l (位移)为变量 [1],如图1所示。
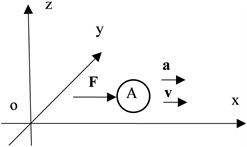
Figure 1. Object A moves in a straight line with uniform acceleration under the constant force F
图1. 物体A在恒力F作用下做匀加速直线运动
作用力F使物体A产生了加速度a,进而有了速度v和位移l。位移l既是空间的体现,又是速度v对时间t的积累,而速度v又是加速度a对时间t的积累。可以说通过力的作用,使空间和时间的变化体现在物体运动中,也就是说对物体施加作用力会使物体处在变化的时空中。
物体A相对参照系所在时空体现出来的能量即动能
(1)
动能公式中既隐含有时间变量t,又隐含有空间变量l,将Ek对时间t求偏导
对时间t再次求偏导
(2)
式(2)中
为动能对时间的二阶偏导数,是反映物体动能瞬间加速变化趋势的物理量,与物体加速
度大小的平方成正比。为了分析方便,将其命名为新的物理量动能势(标量)。可以证明动能势和参照系的选择无关,而且大于或等于0。
将Ek对位移l求偏导
[3] (3)
式(3)表明,
作为动能对空间变量l的一阶偏导数,反映了物体动能对l的瞬间变化趋势,同时它又等于作用力F,是F的一种表达形式。
由式(3)可得
,即
(4)
由式(2)和式(4)可得
(5)
式(5)是一个初速度为0的物体作匀加速直线运动时质量、动能与作用力关于时间和空间的二阶偏微分方程,体现了各物理量之间的瞬间关系。
虽然式(5)是从静止物体受恒力作用做匀加速直线运动推导而来,但对任何形式的运动,在
时都可以近似为直线运动,在
时物体所受作用力都可以近似为恒力,另外从数学的角度来看,
和
都和物体运动的初始状态无关,所以式(5)也适应其它形式及其它惯性参照系下的运动,体现了处
于运动状态下物体质量、动能与作用力之间的瞬间变化趋势的内在关系。我们称式(5)为质能力时空方程,英文缩写可表示为MEF Equation,它具有以下主要特性:
1) 质能力时空方程是一个反映物体质量、动能与作用力动力学关系的二阶偏微分方程。
2) 质能力时空方程体现了物体质量、动能和作用力三者在时空方面的瞬间变化趋势的内在关系,即:质量是动能的基础,力是产生动能势的原因;反之,动能体现了质量的存在,而动能势则体现了力的存
在。需要说明的是,力(
)和动能势(
)作为一阶和二阶偏导数,是反映物体动能瞬间变化趋势的
物理量,无法体现动能是否存在数量上的变化。做匀速圆周运动的物体,虽然受到向心力的作用存在动能势,但由于向心力的方向时刻在变,并和物体的速度始终垂直,所以物体的动能保持不变。
3) 和公式F = ma相比,质能力时空方程适应范围更加广泛,特别是适应针对微观粒子的动力学分析。
4) 质能力时空方程具有普适的特点,引入相对论效应,也适应对高速变质量物体的研究。
3. 运用质能力时空方程对作用力的分析
3.1. 作用力产生的原理
式(5)质能力时空方程里的
是作用力的一种表达形式,反映了物体动能对空间的变化趋势。
由式(3)和(5),可得
(6)
式(6)表示,作用力的大小等于动能势与质量乘积的平方根。作用力的方向,在Ek增加(或具有增加的趋势)时,“±”取“+”,表示作用力F与位移l方向相同,在Ek减少(或具有减少的趋势)时,“±”取“−”,表示作用力F与位移l方向相反。所以作用力产生的条件就是具有质量的物体动能变化或具有变化的趋势。
位于某参照系的测量者测量到某物体运动速度为恒定值时,被测量物体相对测量者及其所在参照系来说动能既保持不变,也没有变化的趋势,可以判断测量者及其所在参照系和被测物体间不存在相互作用力或者相互作用力合力为零。
从式(6)还可以看出,
与
同时发生。物体如果和外界发生力的作用,将产生动能势。反过
来,如果物体具有了动能势,意味着该物体必定和其它物体发生了力的作用,这种情况比较适合研究微观粒子碰撞时的受力和运动规律。
目前物理界普遍认为自然界中力的发生都是由微观粒子碰撞产生的 [4],而物理学上的碰撞又分为弹性碰撞和非弹性碰撞,弹性碰撞遵守动能守恒和动量守恒原理,非弹性碰撞只遵守动量守恒原理,动能不一定守恒,碰撞后的总动能有可能小于或大于碰撞前的总动能 [1] [4]。
3.2. 作用力的斥力与引力属性分析
为了方便,假设两微观粒子P1、P2碰撞前速度方向相反,且在一条直线上,并以其中碰撞的一方P1为例分析其受力特点。
第一种情况,微观粒子之间发生弹性碰撞,遵守动能守恒和动量守恒原理,如图2所示,微观粒子P1、P2发生弹性碰撞,对P1来说,如果碰撞前后速度方向保持不变,那么在碰撞过程中其速度将下降,其动能Ek1也将减少,式(6)中的“±”取“−”,所以P1受到的作用力
(7)
即碰撞中F1与位移l1方向相反,相对粒子P2,粒子P1所受作用力为斥力。
如果碰撞前后P1的速度方向发生改变,那么在碰撞过程中P1将由碰撞前速度逐渐变为0,然后速度反向,由0变为碰撞后的速度。速度反向之前,对P1的受力F1的分析同式(7),为斥力。速度反向之后,速度大小将由0变大,P1的动能由0变大,这时式(6)中的“±”取“+”。由于P1速度方向改变,P1的位移方向也将改变,和原来的位移方向相反。设l11为P1方向改变前的位移矢量,和式(7)里的位移l1方向相同,l12为P1方向改变后的位移矢量,和l1方向相反,则速度反向后P1受到的作用力
(8)
式(8)说明P1速度方向改变后所受力方向和式(7)一样,仍为斥力。
综上,不管微观粒子在弹性碰撞中运动方向是否改变,其受到的作用力都为斥力。
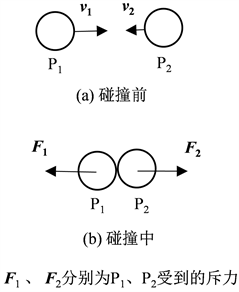
Figure 2. Repulsion is generated when microparticles P1 and P2 collide elastically
图2. 微观粒子P1、P2发生弹性碰撞时产生相互斥力
第二种情况,微观粒子发生动能变小的非弹性碰撞。由于动能变小,同第一种情况类似,非弹性碰撞粒子所受作用力为斥力。
第三种情况,微观粒子发生动能变大的非弹性碰撞。如图3所示,假设P1粒子碰撞后动能变大,速度有所增加,式(6)中的“±”取“+”,其受到的作用力
(9)
即碰撞中F1与位移l1方向相同,相对粒子P2,粒子P1所受作用力为引力。

Figure 3. Attraction is generated when particles P1 and P2 collide in elastically with increasing kinetic energy
图3. 微观粒子P1、P2发生动能增加的非弹性碰撞时产生相互引力
关于二粒子碰撞时发生动能增加的原因,应该和发生这种碰撞的微观粒子的特性有关。由于两种粒子具有亲和性,它们接触时具有相互结合的趋势,和完全非弹性碰撞时被动结合在一起的情况不同,这种结合是主动的,可视为一种势能,二者碰撞时,这种结合势能迅速转化为动能,导致碰撞后一方动能有所提高,而另一方则充分和对方融合并失去物理独立性 [1],这也是自然界万有引力、电磁引力以及其它引力发生的根本原因。比如万有引力,参与万有引力的引力子与任何其它带质量粒子相遇时,结合势能迅速转化为动能,并与对方融合在一起而失去物理独立性。正是由于引力子会和探测器的微观粒子迅速融合而“消失”,所以很难探测到单独存在的引力子 [4] [5]。
以上三种情况分析的是微观粒子的受力,对于宏观物体而言,其受力其实是微观粒子所受微观力的矢量和,微观力的作用力属性决定了宏观力的作用力属性,宏观物体之间的作用力可分两种情况来分析。
第一种,宏观物体内部趋于固定排列的微观粒子几乎同时受到外来分散分布的微观粒子的碰撞,产生众多微观力,这些微观力的矢量和表现为宏观物体受到的宏观力。
设物体受到的宏观力为F,Fi为组成宏观物体的第i颗微观粒子所受到的微观力,根据质能力时空方程和式(6)
(10)
(11)
由于我们肉眼看不到外来分散分布的微观粒子,只能看到宏观物体,所以这种力宏观上表现为非接触力,即宏观物体受到了产生分散分布微观粒子的物体的非接触作用力,也就是我们通常说的场力,微观粒子在空间的分布规律体现了场的特点。场力实际上是众多微观力在宏观物体上的体现,本质上还是微观力。式(10)的“+”或“−”决定了场力的属性引力或者斥力。
从场力的产生原理可以看出,宏观物体所受到的场力是多个微观力的矢量和,万有引力就是这样的
场力,公式
就是对宏观物体受到的这种多个微观力的矢量和的宏观表达 [1]。
第二种,宏观物体与宏观物体间的宏观接触力。从微观的角度分析,宏观接触力是由于受力物体和施力物体一部分表面微观粒子发生碰撞而产生的,这些表面粒子继而与物体内部其它粒子发生碰撞,将微观力传递到物体的其它粒子,宏观上表现为物体整体受力。所以宏观物体与宏观物体间的宏观接触力本质上也是微观力,是微观力的另外一种矢量和表现。
3.3. 自然界的四种基本作用力
目前普遍认为自然界存在四种类型的基本作用力,它们是万有引力、电磁作用力、弱相互作用力和强相互作用力 [4] [6]。从微观粒子的角度分析,自然界的四种基本作用力都可归纳为3.1节中描述的微观力,即微观粒子之间的碰撞作用力 [4]。具体为:
1) 万有引力通过带质量微观粒子与引力子之间的碰撞而产生,为长程力;
2) 弱相互作用力通过强子、轻子等费米子和W、Z中间玻色子的碰撞而产生,为短程力;
3) 电磁作用力通过带电微观粒子和光子的碰撞而产生,为长程力;
4) 强相互作用力通过强子(夸克)和胶子的碰撞而产生,为短程力。
包括量子力学、量子场论等在内的量子理论具体研究和分析了各种微观粒子碰撞时力的产生及能量
与质量的变化的物理过程和遵循的规律,如果对应到各相关粒子的
与
,则都应满足质能力时空方程式。
从式(6)可以看出,作用力F的大小与动能对空间的偏导
以及动能对时间的二次偏导
的平方根成正比,所以作用距离越小、作用时间越短,
、
就相对越大,对应的相互作用力F也就相对越大,相互作用的反应率和无量纲耦合常数也就越大 [4],见表1。

Table 1. The ratio of dimensionless coupling constants, reaction rates and relative magnitude of the four fundamental interaction forces
表1. 四种相互作用力无量纲耦合常数、反应率大小及强度之比
表中采用了自然单位制,ħ = c = 1,其中c是光速,ħ是约化普朗克常数。me及mp分别为电子及质子的静止质量,G为万有引力常数,e为电子电荷,GF为费米弱相互作用耦合常数,g为汤川强相互作用耦合常数 [4]。
3.4. 万有引力
量子理论对弱作用力、电磁作用力和强作用力都有了很深入的研究,形成了很成熟的、已经得到实验相当严格检验的规范场理论,像电弱统一理论、量子色动理论等 [8] [9]。本节从质能力时空方程的角度重点分析一下万有引力的作用原理。
万有引力定理告诉我们相距为r、质量分别为M和m的两物体A、B之间的万有引力为
G为引力常数 [1] (12)
分别代入物体A、B的质能力时空方程,可得
由以上两式可得
(13)
式(13)说明A、B两物体通过万有引力相互作用时,一方的动能势与对方的质量成正比,也就是它们彼此受到了与对方质量有关的某物理量的影响而形成相互之间的作用力,进而导致彼此产生动能势。这个物理量在量子力学和广义相对论里有不同的描述。
从量子力学的角度看,体现这种物理量的应该是“引力子” [4]。物体A产生的引力子(空间密度与A的质量M成正比)和构成物体B的微观粒子发生动能增加的非弹性碰撞而产生微观引力,引起B各粒子
产生微观动能势,这些微观动能势合在一起就形成了B物体的宏观动能势
,同理A物体也会由于物体B产生的引力子(空间密度与B的质量m成正比)与A的粒子碰撞而形成自己的宏观动能势
,
如式(13)所示,A、B物体各自的宏观动能势与对方的质量成正比。A、B物体之间的微观引力合在一起就形成了A、B物体之间的万有引力。
从广义相对论来看,体现这种物理量的是“时空弯曲效应”,在广义相对论里有详细分析,也就是物体A与物体B彼此受到了与对方质量成正比的时空弯曲效应的影响 [10],这种影响导致了物体微观粒子产生微观动能势而产生微观引力,它们的矢量和就是万有引力。
综合量子力学和广义相对论,我们认为,具有质量的物体的周围分布着(或者说不断向周围产生)一种和物体质量有关的微观粒子,即“引力子”。假设物体为均匀球体,引力子在空间的分布密度与离开物体球心的距离的平方成反比,和物体质量成正比。广义相对论的时空弯曲正是引力子在空间的分布密度不同造成的。量子力学中描述的“引力子的空间分布的不同密度”等效于广义相对论的“时空弯曲”,由此就形成了经典力学描述的物体之间的引力场,进而就产生了万有引力。
3.5. 物质的形成与变化
自然界各种力产生的根本原因就是微观粒子之间的碰撞,而碰撞过程中动能是否增加(或具有增加的趋势)决定了微观粒子之间作用力的性质是引力还是斥力。各粒子在碰撞后运动状态将发生变化,有的做非圆周运动,相互远离,有的结合在一起形成新的粒子,有的持续受到场力的作用而相互环绕,形成复合粒子。量子理论认为构成物质的基本粒子(即轻子和夸克)是费米子,而玻色子是力的传递者,通过玻色子与费米子的碰撞形成各种相互作用力,使费米子形成各种复合粒子,进而形成各种形态的物质与状态 [4]。当然这些微观力的作用过程也可以逆向进行,使相应的微观粒子产生各种变化,比如聚变、裂变与衰变等,产生其它复合粒子、基本粒子或无质量粒子等,形成新的物质与状态 [4] [5] [6]。
4. 运用质能力时空方程对质量的分析
4.1. 质量是动能在时空中变化的体现
由质能力时空方程式可得
(14)
从式(14)可以看出,质量体现为物体动能对空间的一次偏导的平方与对时间的二次偏导的比值,也就是说质量的本质是物体动能相对时空变化的体现。
从第3.1节作用力产生的原理我们知道,位于某参照系的测量者测量到某物体运动速度为恒定值时,被测量物体相对测量者及其所在参照系来说动能既保持不变,也没有变化的趋势,可以判断测量者及其所在参照系和被测物体间不存在相互作用力或者相互作用力合力为零。通过本节对质量本质的分析,我们也可以判断,位于某参照系的测量者测量到某物体运动速度为恒定值时,被测量物体相对测量者及其所在参照系来说无质量或者说质量没有意义。
由第2节我们知道,作用力是粒子在相互碰撞时产生的。在碰撞过程中,比值
如果保
持不变,粒子的质量也将保持不变,这时的碰撞反应遵守必要的守恒原理,包括能量守恒、质量守恒、动量守恒等 [4] [5] [6]。
粒子在碰撞过程中如果能量足够大,粒子所受到的力足够大,引起比值
发生变化,则
粒子的质量也将发生变化,也就发生了常说的质量的生成或湮灭。这时的碰撞质量和能量不再分别守恒,通过爱因斯坦质能方程E = mc2,能量和质量可以互换,质量和能量之和守恒 [2]。
4.2. 正反粒子碰撞
粒子碰撞过程中比值
发生变化的一个典型例子是正反粒子的完全非弹性碰撞。设粒子P1和粒子P2互为反粒子,静止质量都为m,电性相反,二粒子通过吸引力相互靠近。
P1的质能力时空方程为:
P2的质能力时空方程为:
由于粒子P1和P2互为反粒子,相互吸引,二者相遇时将会以不断增加的吸引力(光子和引力子形成的场引力)和速度无限靠近,由于二者质量相等,各种物理参数相同或对称,在无限靠近的某瞬间将变为相互静止并结合在一起,属于完全非弹性碰撞 [1],设二者结合形成的组合体为粒子P0,则其质能力时空方程为:
(15)
由于粒子P0为粒子P1和P2结合所得,所以在碰撞过程中P0的动能对空间的变化应等于P1和P2动能对空间变化之和,即
(16)
P1和P2互为反粒子,以相同速度相互靠近,能量相等,位移相反,所以在碰撞过程中Ek1 = Ek2,l1 = −l2。即
代入式(15)
(17)
粒子P0为粒子P1和P2结合所得,所以碰撞过程中
(18)
由于t0 = t1 = t2,而动能Ek0和时间都为标量,所以
(19)
由式(17)、式(19)可得
由此可见,正反粒子P1和P2相遇后生成的新粒子P0质量为0,也就是在正反粒子P1和P2变为相互静止的一瞬间质量都变为0,从质能力时空方程特性第2条我们知道质量是动能的基础,失去质量的动能Ek将以其它形式的能量存在,这种形式就是光子的电磁能。这时就发生了正反粒子P1和P2质量的湮灭,而湮灭的质量变成了带电磁能的光子 [4] [8]。
如果发生完全非弹性碰撞的粒子不是正反粒子关系,由于二者质量等各项物理参数不完全相同或对称,导致碰撞过程很复杂,比如在碰撞过程中,对体积相对较小的粒子来说,大体积粒子不能完全当成质点考虑、碰撞时间相对较长、速度不能同时相对为0,等等,所以这种碰撞很难实现彼此质量的瞬间湮灭,这里不做详细讨论。
4.3. 高能光子碰撞
高能光子之间的弹性碰撞是粒子碰撞过程中比值
发生变化的另一个典型例子。设粒子
P1和P2都为高能光子,它们发生正面碰撞,实验证明这种碰撞为弹性碰撞,它们将交换速度而分离 [1]。
P1的质能时空方程为:
(20)
P2的质能时空方程为:
(21)
发生碰撞前,由于光子以恒定频率和光速运动,能量保持不变,P1和P2对应的
、
、
、
都为0,这时它们的质量m1、m2没有实际意义。
发生碰撞后,二者交换速度而分离,碰撞过程中P1和P2的速度将由光速变为0,然后再反向运动,在这个过程中,二粒子的能量都将随时间和空间发生很大的变化,
、
、
、
都将变为非0值,碰撞后P1和P2的质量m1和m2具有了实际意义,并可由以下两式分别求出:
(22)
(23)
也就是说,粒子P1和P2都由光子变为了有质量的粒子,动能相对时空的变化体现为质量的存在。实验证明,光子能量足够大时,二者的碰撞有可能生成了带质量的电子或其它粒子对 [4] [8]。
5. 总结
质量、动能与作用力关于时空的二阶偏微方程(MEF Equation),
,反映了质量、动
能与作用力之间的内在联系,也反映了三者关于时空的瞬间内在关系。
质能力时空方程揭示了目前已知的四种基本作用力的本质,即作用力是微观粒子间相互碰撞的结果,引力产生于动能增加或具有增加趋势的非弹性碰撞,而斥力则产生于其它类型的碰撞。
万有引力是引力子与带质量粒子相遇时和对方迅速结合,并将结合势能转化为动能的结果。正是引力子的这种特性导致引力子很难被探测到。不过引力子是客观存在的,它形成的引力波已被观察到。相信随着科技的发展,在不久的将来一定能确切探测到引力子的存在。
质能力时空方程揭示了质量的本质,即质量是物体动能相对时空变化的体现,表现为物体动能对空间的一次偏导的平方与对时间的二次偏导的比值,该比值的变化意味着质量的产生或湮灭。高能光子相撞产生实物粒子以及正反粒子相互湮灭是这种比值极端变化而引起质量变化的具体例子。