1. 可再生能源发电参与电力市场调度现况
现阶段我国新能源发展势头迅猛,新能源渗透率远超于同期部分发达国家。2020年,我国新增风电装机7167万千瓦、太阳能发电4820万千瓦,风光新增装机之和约为1.2亿千瓦 [1],远超市场预期。然而受一次能源限制,风电、太阳能发电具有显著的季节特性和随机、波动特征,对电力电量的跨季节分配、日内调整和实时平衡等不同时间尺度的灵活资源提出了更高要求。
我国政府实行电力改革,电力市场调度由发电侧传统能源发出电能的多少,这样一组可控变量控制用电侧用户消耗电能,这样一组随机变量的过程转变为发电侧传统能源、可再生能源发出电能与用电侧用户消耗电能,这样两组随机变量动态平衡的过程 [2]。那么在电力市场中,电价的高低,不仅依据市场环境,还取决于竞争对手的定价策略。通过纳什均衡的求解,来确定在电力市场中,各发电商应如何进行定价才能实现利润最大化。是个复杂的自适应的过程,更是多方博弈的一个问题 [3]。结合国内外运行范例通过数据分析,预测负荷曲线,以储能电站、火电调峰为基本手段,建立风火联合、光火联合模型对负荷波动进行调节 [4] [5]。为此在新能源出力过大的情况下,亟需在高比例新能源接入的电网中引入新的调峰电源以保证系统动态平衡性 [6]。文献 [7] 对国内储能现状进行研究,分析储能电站的调峰成本。文献 [8] 采取根据电能申报属于对日前市场预出清,计算深度调峰需求量,然后根据深度调峰需求量计算各机组发电计划及火电机组的深度调峰量。类似的,文献 [3] 提出一种光热发电–火电联合调峰的优化控制方法。论述光热发电的可调节特性以及光热发电–火电联合调峰的可行性,并通过实例仿真验证优化控制方法的有效性。
2. 可再生能源证书(REC)定价模型
2.1. REC价格变化与市场需求的关系
REC的价格由政府决定,政府采用直接或间接补贴形式,但这种方式往往难以掌握可再生能源的发电成本变化 [10],补贴金额不随市场交易变化波动大,费时费力。为此研究REC的价格与市场需求的关系,以市场的手段确定REC的价格曲线。如图1,通过对电力市场耗能曲线的分析得出可再生能源证书的交易量与需求量的关系,其需求曲线和边际利润曲线近似一条折线,对于不同的交易量其折线的斜率不同,而成本曲线近似于抛物线。
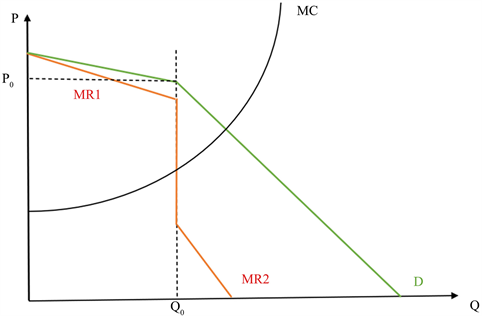
Figure 1. Relation between REC pricing curve and market demand
图1. REC定价曲线与市场需求的关系
如图1所示,图中横坐标代表交易电量Q,纵坐标代表成本价格P,折线D代表需求电量,根据利润最大化原则,MR = MC时,寡头能实现其利润的最大化,即在拐点Q0时存在最大利润,其对应的Q0就是该产品的最优价格。
2.2. 曲线平移对REC的影响
由政府制定REC价格,考虑到光伏的REC高于风力发电,长此以往,将导致市场向风力发电倾斜 [11]。为此,REC的价格应该由市场决定,通过供给–需求曲线求得。在寡头市场中,当市场边际成本等于市场边际收益时,利润最大。总收入可以表示
(1)
假设需求曲线函数为:
(2)
边际收益曲线函数为:
(3)
如图2所示,当需求曲线固定为D0时,交易量为Q0,市场价格为Q0,当成本价格升高时,若升至曲线MC1,交易价格不变,仍为Q0。只有当成本价格发生明显变化时,例如升至曲线MC3或降至曲线MC2,交易价格才变为Q3或Q2。
其需求曲线和边际收益曲线可以表示为
(4)
(5)
供给曲线表示为

Figure 2. Influence of demand curve changes on REC pricing
图2. 需求曲线变动对REC定价的影响
(6)
为此,在满足在Q0处满足
且
时,Q0可以确定
(7)
当成本升高,即
时,求边际成本及边际收益两曲线的交点
(8)
可以得到
(9)
代入求得可再生能源证书价格Q为
;同理可以得到当成本大幅下降时,可再生能源证书价格Q为
。
若把碳排放配额考虑进来,经ETS与REC综合考虑研究可再生能源证书定价,当REC价格低于碳排放价格,市场投机者可能会大量购买REC,作为碳配额排放。针对这种情况下,如图2所示,我们将供应曲线固定为MC0,当需求急剧增加时,需求曲线与边际收益曲线分别调整为D1与MR1,此时,REC交易价格升高至
,为此可有效遏制这种投机行为。此时,需求曲线及边际收益曲线可表示为
(10)
(11)
可再生能源证书REC价格最终确定为
。
2.3. 可再生能源证书交易模型
基于博弈论来构建可再生能源证书的交易模型,该模型利用相对成熟的碳市场带动发展可再生能源证书的交易市场。对于电力市场竞争中的三个主要参与者,即P2G设备、可再生能源发电厂和火力发电厂 [12] [13]。
2.3.1. 每个参与者的利益模型
在发电侧竞价策略中将ETS与REC统筹考虑,将碳排放配额与可再生能源证书的交易纳入发电成本计算。
1) P2G设备收益
P2G设备收益包括销售天然气及氢气的收益及碳排放配额的收益减去购电支出
(12)
式中,
为P2G的集合,
为售出气体的价格,
为售出气体量,
为购入电量的节点电价,
为购入电量,
为碳价,
为P2G的减排因子。
约束条件为:
(13)
(14)
(15)
(16)
上式分别是单位时间内购电和售气量的能量平衡及各出力边界限制,其中η表示转化效率。
2) 可再生能源发电厂收益
(17)
可再生能源的收益分为两部分,一部分为售出电量与节点电价的乘积,另一部分为销售REC获得的收益。式中,
为节点电价,
为REC的价格。约束条件为:
(18)
(19)
可再生能源发电主要受能量平衡及调度电量的制约,并存在弃风弃光现象。
3) 传统火力发电厂收益
火电厂的收益等于售电收入与购买REC及碳排放配额的差值。
(20)
约束条件为
(21)
若发电厂的碳排放量减去REC转化的配额以及政府分配的配额即为发电厂需要购买的配额数量。
2.3.2. 基于碳交易和REC交易的发电侧竞价策略
在得到各个电力市场参与者的收益模型之后,建立可在再生能源与P2G合作模型,P2G设备的购电量可以从可再生能源发电机组处获得,既促进了可再生能源的消纳,又节约了P2G设备的购电成本 [14]。这样使得基于碳排放和可再生能源政策限制的交易,是在火力发电厂与可再生能源与P2G两者组成的整体之间进行的。
其模型可以表示为:
(22)
式中,
,
,
分别代表火电,光伏和风电的竞标价。
约束条件:
(23)
(24)
此竞价模型又可以作为约束条件补充至各收益模型在得到三个参与者的单层收益数学模型后,例如P2G设备的收益可以重新表述为
(25)
根据演化博弈理论,P2G与可再生能源发电企业采取合作博弈与火力发电厂参与市场竞价,根据迭代过程,可以找到系统纳什均衡点
。
3. 算例及分析
3.1. 参数设定
为验证可再生能源发电企业与P2G合作博弈在电力市场竞争中的竞争优势,本文构建了一个火电企业、可再生能源发电企业、P2G三者参与电力市场竞争的竞价模型,仿真使用的主要参数如表1,其数据取自南方电网调度运行网站。

Table 1. Simulation parameter settings
表1. 仿真参数设定
本次竞价模拟算例设计如表2所示。
3.2. 计算结果
本文通过图3的三个算例,验证本文构建的双层模型与传统调度模型,对促进可再生能源消纳以及火力发电调度两方面的影响。在算例设计中,主要是引入两个变量:REC证书交易与合作博弈,以市场是否为寡头市场探究REC交易对新能源消纳的促进作用,以采用P2G与可再生能源发电厂合作与各发电企业独立竞价探究合作博弈对电力市场竞价方收益的影响。
本章提出的发电侧报价策略模型属于非线性,混合整数优化问题,对上层模型进行线性化处理并使用粒子群算法进行优化求解 [15],生成当前市场价格下各发电企业报价策略。上层优化结果传递至下层使用CPLEX求解器进行现货市场出清,得到各类型交易市场出清价格。若现货市场出清价格发生改变,则将下层出清得到的现货市场价格返回至上层生成新的储能报价,然后继续传递至下层进行现货市场出清。上下层间重复进行迭代直至现货市场出清价格趋于稳定,输出当前电力市场报价中标情况计算其获得的最大收益,并输出发电侧的最优报价策略。具体的求解流程如图3所示。
本模型设计要使可再生能源、传统燃煤企业及P2G设备各发电商的受益最大,且系统总消耗最小 [16]。为此需求出目标函数式(2-16)的拉格朗日函数,如式26,利用其拉格朗日函数,研究系统收益受到的来自市场竞争环境各方面的制约。
(26)
各机组的出力共分为三个部分:传统燃煤、光伏及风电的出力限制,碳排放配额及REC交易的额度输出与买入,机组出力上下限的限制。如图4所示。
由图4可以看出,1) 算例1未出售的REC证书曲线明显高于算例2,这表明,在电力市场中优先考虑发电的绿色属性,有利于REC的消纳。2) 从火电机组的出力曲线来看,算例2的火电机组出力曲线更平滑,REC交易可以有效地促进可再生能源的消纳,从而使火电机组紧急调峰的现象明显减少,调峰曲线更加平滑。
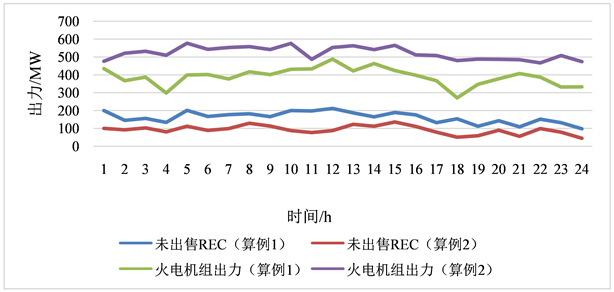
Figure 4. Output of thermal power units and REC certificate transactions
图4. 火电机组出力及REC证书交易情况
在考虑传统燃煤企业碳排放系数、可再生能源出力率、P2G减排因子、碳配额转换比等多种因素后,以表1相关数据为依据,各发电机组的收益可以表示为
目标函数:式(26)。
约束条件:式(16)——(25)。
由图5,在电力市场环境中引入REC交易,极大的促进了可再生能源的消耗,提高了系统总收益。对比算例2与算例3同等市场竞争环境下,P2G参与市场竞价与可再生能源或火力发电相比,收益方面差距明显。
3.3. 结果分析
通过上一节对三个算例的分析可以看出,1) 相比市场完全竞争,将REC交易引入市场竞争,优先考虑政府制定的绿证政策,使可再生能源发电商的收益不仅来源于售电收益,还有一部分来源于绿证收益,从而增加了可再生能源的消纳。2) 将P2G引入市场竞争,可再生能源发电企业与P2G合作参与市场竞争,以碳排放政策带动REC的交易,使可再生能源发电企业更具市场竞争力。

Figure 5. Earnings of each participant in the market competition
图5. 参与市场竞争各参与者的收益
如图6所示,在同一坐标轴下,随着可再生能源证书的价格不断升高,可再生能源的利用率反而进一步提高了,并且碳排放量逐步下降。这说明,电力市场中引入REC交易,有效遏制了发电企业的碳排放总额,间接提高了火电厂的发电成本,增加了可再生能源发电企业的市场竞争力。
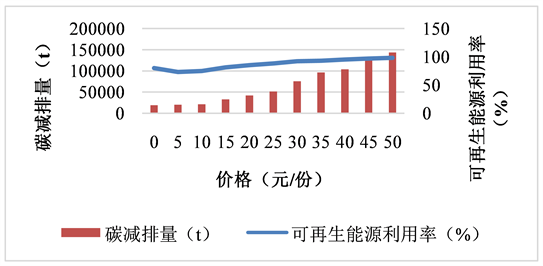
Figure 6. Relationship between REC trading and renewable energy consumption and carbon emissions
图6. REC交易与可再生能源消纳及碳排放量的关系
为此,要真正的促进可再生能源的消纳,则需要选择合适的可再生能源证书定价,如图7所示,对于不同的市场碳排放配额比例下,REC定价对可再生能源利用率和碳排放总量与的影响。
在同一坐标轴下,以折线图表示REC定价与可再生能源利用率的关系,以柱状图代表REC定价与系统碳减排量的关系。1) 可再生能源配额比例一定,随REC定价价格的升高,可再生能源消纳比例上升,碳排放总量下降,并在一定价格时趋于饱和。可再生能源配额比例越大,趋势变化越快。2) 对于较高比例的可再生能源配额,在同一REC定价的前提下,其碳减排总量及新能源利用效率反而不如低比例的可再生能源配额机制高。
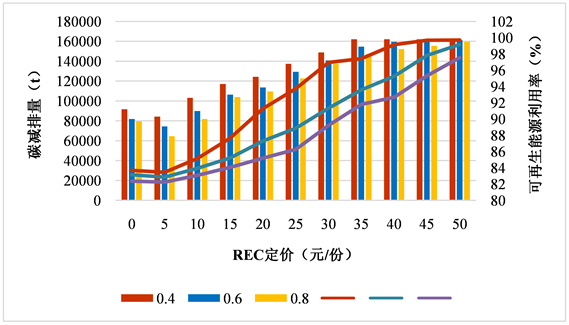
Figure 7. Coordination between REC price and carbon emission and renewable energy consumption
图7. REC价格与碳排放及可再生能源消纳的协调关系
4. 结论
本文结合电力市场交易中政府制定的ETS与REC两种政策,并将P2G作为市场主体,引入市场竞价。建立了P2G联合可再生能源发电与传统燃煤企业的双层博弈模型,以发展较为成熟的ETS交易机制带动REC的购买力,同时P2G与可再生能源发电相结合参与市场竞争,增加了可再生能源的市场竞争力,节约了发电成本,提高了企业收益。
项目基金
山东省高等教育本科教学改革研究项目“基于互联网思维的层级式教学模式探究与实践”(编号:M2020145)