三轴激光切割方形件组批排样优化建模研究

Research on the Optimization Modeling of the Three-Axis Laser Cutting of Square Parts

摘要: 激光切割在处理大件原材料方面具有巨大优势，在激光切割方形件的生产中，排样优化与订单组批问题一直是企业节约原材料和能源使用的关键。在充分考虑其约束并建立其混合整数规划模型后，本文首先按产品的规格即长或宽的尺寸进行分类，将长度或者宽度相同的产品项归为一类，给予它们同一个型号，并排列成一个更大的产品项(item)组成一个栈(stack)。然后将栈(stack)按照从大到小的顺序依次组成条带(stripe)，直到达到条带(stripe)长度限制下的条带长度最大值。最后对得到的条带(stripe)进行预处理并利用遗传算法求出可行的排样方式。通过与传统按照每个产品项的ID进行全排列并对其使用遗传算法求解方法对比，本文提出方法使得板材有效利用率提高了近15%，同时也大大提高三轴激光切割的工作效率。

Abstract: Laser cutting has great advantages in processing large pieces of raw materials. In the production of laser cutting square pieces, layout optimization and order batching have always been the key to saving raw materials and energy use for enterprises. After fully considering its constraints and establishing its mixed-integer programming model, this paper first classifies products according to their specifications, that is, length or width, classifies products with the same length or width into one category, gives them the same model, and arranges them into a larger product item to form a stack. Then, the stack is formed into strips in order from the largest to the smallest, until the maximum strip length under the strip length limit is reached. Finally, the strip is preprocessed and a feasible layout method is found by genetic algorithm. Compared with the traditional method of arranging the ID of each product item and using genetic algorithm to solve it, the method proposed in this paper improves the effective utilization rate of the plate by nearly 20%. At the same time, it also greatly improves the working efficiency of three-axis laser cutting.

1. 引言

制造业是我国国民经济的支柱产业，是立国之本、国之利器。强国战略的第一个十年行动纲领便是“中国制造2025”。所谓智能制造，就是在客户产品需求大、订单规模多、单件尺寸大且产品质量要求高时，企业为其提供“个性化定制”的服务。方形件就是其中之一，由于企业订单数量庞大，生产组织通常采用订单组批、批量生产、订单分拣、材料排样的模式，通过这种集成模式来实现批量切割，提高原材料利用率和激光切割效率。

近几十年，每年在各类运筹学、管理学、制造、计算机等领域的高级别刊物中，都有大量关于各类切割填充问题的算法和技术报道。线性规划、整数规划、分支定界、动态规划、递归、启发式算法、智能算法等众多技术与算法都应用到方形件切割与填充问题中 [1] [2] [3] ；法国巴黎大学的Hifi等主要研究排样问题，采用多种不同的算法求解圆形和矩形的两阶段排样问题 [4] [5]。订单组批与排样优化尤为重要。订单组批是将不同订单组成若干批次，实现订单的批量化生产。既要提高生产订单的效率，又要满足客户的交付要求，降低企业的订单分拣难度。在考虑订单交货期、设备产能负荷、仓储容量、材料利用率、生产效率、生产工艺约束等因素下，对生产订单进行组批优化。使具有相同材质、交货期相近、工艺相似的订单安排在同一个生产批次，通过订单组批优化来保证交货期，提高原材料的利用率，提高设备生产效率等。排样优化旨在合理规划方形件在板材上的布局，以减少下料过程中的板材浪费，简化切割过程。作为企业在生产方形件的第一步，下料浪费的材料和资源巨大，如何提高材料利用率，降低损耗，是企业减少浪费、增加收入的关键 [6] [7] [8] [9]。

2. 订单批次与排样优化

由于订单交货期、材料利用率、生产效率等因素，需要对生产订单进行组批优化 [10] [11]，使的相同材质、交货期相近、工艺相似的订单在同一个生产批次，以此来保证交货期，提高原材料利用率及设备生产效率。

对于排样优化，有齐头切和非齐头切两种切割方式，其中齐头切因为排样方式的不同，又可以细分为三阶段非精确(3NE)排样方式、三阶段匀质排样方式(3E)、三阶段同质排样方式(3H)。其中3E和3H属于精确排样方式。根据工艺要求，本文对三阶段的齐头切排样方式进行排样优化，即每次都为直线切割，每次切割使得板材分成两块，第一阶段生成stripe (条带)；第二阶段对stripe进行切割，生成stack (栈)；第三阶段对栈切割，生成item (产品项(item))。如图1所示：

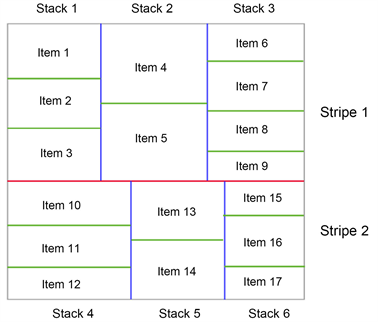
Figure 1. Formal definition of different cutting stages

图1. 不同切割阶段的形式定义

3. 模型建立与求解

3.1. 模型假设与约束

3.1.1. 模型假设

根据厂家和厂商要求，有如下假定：

1) 只考虑齐头切的切割方式(直线切割、切割方向垂直于板材一条边，并保证每次直线切割板材可分离成两块)；

2) 切割阶段数不超过3，同一个阶段切割方向相同；

3) 排样方式为精确排样；

4) 假定板材原板材仅有一种规格且数量充足；

5) 排样方案不用考虑锯缝宽度(即切割的缝隙宽度)影响；

6) 所有订单的交货期均相同，不做区分。

3.1.2. 模型约束

在满足订单需求以及以下约束的情况下进行排样优化，使得原板材的使用尽可能的少。

约束：

1) 在相同栈(stack)里的产品项(item) (item)的宽度(或长度)应该相同；

2) 最终切割生成的产品项(item)是完整的，非拼接而成。

3.2. 模型建立

根据某厂的生产方形加工件的4组订单数据A (A1, A2, A3, A4)，有如下设定：

1) 待切原板材的板材尺寸L * W，其中原板材长度L = 2440 (mm)，原板材宽度W = 1220 (mm)，题中给定板材原板材数充分，且单个批次产品项(item)总数上限为1000，单个批次产品项(item)的面积总和上限250 m²。

2) 设定需要排样的产品项(item)的类型为有n种且每种产品项(item)的长、宽和需求量分别为 $l_i$ 、 $w_i$ 、 $d_i$ ，其中i为产品项(item)的型号。

3) 相同长度或者宽度的产品项(item)虽然id是不一样的，但是可以视为同一种产品项(item)，因此给与它们同一个型号。

因此可以用一个合理的三阶段排样方式，使用数量最少的原板材，从而排样全部数据集给出的所有订单。

以使用板材数量最少为目标进行二维三阶段切原板材，用混合整数规划模型表示 [10]。建立的数学模型如下所示：

$\min D={\displaystyle \underset{j=1}{\overset{R}{\sum }}{x}_j}$ (1)

$\text{s}\text{.t}\text{.}\{\begin{array}{l}{d}_i={\displaystyle \underset{j=1}{\overset{R}{\sum }}{a}_{ij}}{x}_j,i=1,2,\cdots ,n\\ x_j\in N,j=1,2,\cdots ,R\end{array}$ (2)

式中：R为原板材切割时的排样方式；

D为原板材数量；

$a_{ij}$ 为第j种排样方式上所包含的i型产品项(item)数量；

$x_j$ 为第j种排样方式的使用频率，即有多少块原板材按照第j种排样方式进行切割；

$d_i$ 为每种产品项的数量。

对于如何排样这里提出了两种方法：

1) 传统方法：对每个产品项的id进行全排列的随机排样，仅考虑每个产品项的id，对每个产品项的id进行全排列，用遗传算法求得排样方式的最优解。这种全随机排列id的算法可以解出理论全局最优解，但是在实际求解过程中，很容易落入局部最优解，不能求出最优解，最后结果得出的板材有效利用率很小。

因此在传统方法的基础上做了改进得出本文使用的方法。

2) 本文方法：忽略产品id，先按产品项的长或宽的尺寸进行分类，分类之后在逐步排样成原板材。根据模型假设要求，排样方式为精确排样且切割阶段不超过3阶段，要求同一个栈(stack)里的产品项(item)的长度或者宽度相同，因此将数据中具有相同长度或者宽度的产品项(item)归为一类，给与它们同一个型号，并排列成一个更大的产品项(item)组成一个栈(stack)。然后将栈(stack)按照从大到小的顺序依次组成条带(stripe)，直到达到条带(stripe)长度限制下的条带长度最大值。最后对得到的条带(stripe)进行预处理和全排列并利用遗传算法求出最优的排样方式。本方法的排样方式流程图如图2所示：

Figure 2. Flow chart of layout method

图2. 排样方式流程图

本文中的排样方式一定是保证产品从项(item)到栈(stack)，从栈(stack)到条带(stripe)，在栈(stack)组成条带(stripe)的过程中会产生大量的废料，这样的废料保证最后形成的条带(stripe)是一个矩形，最后从条带(stripe)到整块原始板材。这样的算法一定保证了切割是齐头切的，因此原始板材齐头切才能切成条带(stripe)，条带齐头切才能切成栈(stack)，栈(stack)通过齐头切并切掉废料，最后得到产品项。同时要保证在产品项排列到栈(stack)的过程中，下一个产品项一定是紧贴上一个产品项的，这样就保证了精密排布。

在排样完成和计算最少数量的原材料后，可以用有效利用率来评价切分的优秀程度。有效利用率为所有订单产品项(item)的面积和除以所有原板材的面积和，有效利用率越高越好，在这里可以计算出极限利用率，即理论上最少需要多少板材。对于数据A1，所有订单产品项(item)的总面积和为24.86平方米，计算需要83.54块2440 × 1220的原板材，所以至少需要84块原板材，计算得到的极限利用率为99.45%，因此排样后的有效利用率越接近99.45%越好。

因此有效利用率计算公式为：

$\eta =\frac{n\ast l_i\ast w_i\ast d_i}{L\ast W\ast D}\ast 100\%$ (3)

式中：

$\eta$ 为有效利用率；

n为产品项(item)的种类；

$l_i$ 为每种产品项(item)的长；

$w_i$ 为每种产品项(item)的宽；

$d_i$ 为每种产品项(item)的需求量；

L为原板材的长；

W为原板材的宽；

D为原板材数量。

3.3. 模型求解

3.3.1. 本文方法模型求解

遗传算法是一种通过模拟自然进化过程搜索最优解的方法。该算法通过数学的方式，利用计算机仿真运算，将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程它是模仿自然界生物进化机制发展起来的随机全局搜索和优化方法，相较于一些传统的优化算法，通常能够快速地获得较好的优化结果。本文将产品项一步步组成条带，再对条带数据预处理后进行排样，最后利用遗传算法对所建模型进行优化求解。

以订单数据A为例，具体参数如下：

1) 单个批次产品项(item)总数上限max_item_num = 1000；

2) 单个批次产品项(item)的面积总和上限max_item_area = 250 (m²)；

3) 板材长度plate_length = 2440 (mm) plate_length = 2.440 (m)；

4) 板材宽度plate_width = 1220 (mm) plate_width = 1.220 (m)。

并将数据中数据统一单位为米，参照3.2节新方法建立的模型步骤对其求解。将所有产品项的长宽中，较大的作为新的长度，较小的作为新的宽度。

采用遗传算法，并增加了一步数据预处理的操作，即首先剔除无法与其他任何条带(stripe)组合的条带(stripe)，他们各自占据一个原始板材。然后再对剩余的部分条带(stripe)进行组合。因此剩下只需要对条带(stripe)进行全排列，利用遗传算法进行求解，便可得到最优解。

1) 编码

本问题中采用整数编码的方式实现染色体编码，将可供组合的条带编号，染色体即为这些编号的一个排列。

2) 解码方式

按顺序组合条带，不断将之后的条带拼接到之前的组合体中，直到长度超过样板长度为止，更换新样板，并记录使用的样板数量和组合方式。

3) 评估个体适应度

以使用的板材数量作为该个体的适应度，使用板材越少则适应度越高，该个体越容易被保留。

$\min D={\displaystyle \underset{j=1}{\overset{K}{\sum }}{x}_j}$ (4)

x_j为第j种排样方式的使用频率，即有多少块原板材按照第j种排样方式进行切割。

4) 选择

可用的选择策略有很多，最简单的是对个体进行排序，保留排名靠前的种群，还有轮盘赌选择方法，适应度越高的个体被保留的几率越大。

5) 交叉

交叉操作在这里为交换两个染色体的部分排列顺序，在本题中交叉概率取值为0.7。

6) 变异

变异操作即以较低概率交换一个染色体的部分位置，最后输出结果即为较优的组合方式，根据这种组合方式组合相应的条带，确定板材的排样。在本题中变异概率取值为0.2。

7) 结果分析

在这里同样设定种群大小为400，迭代代数为300代，交叉概率取值为0.7，变异概率取值为0.2，经过迭代优化后适应度函数变化图如图3所示。

3.3.2. 传统方法模型求解

传统方法是按照每个产品项的ID进行全排列然后对其使用上述遗传算法直接求解方法。同样以数据A为例，具体步骤与上述方法相似，此处不再赘述。经过迭代优化后适应度函数变化图如图4所示。

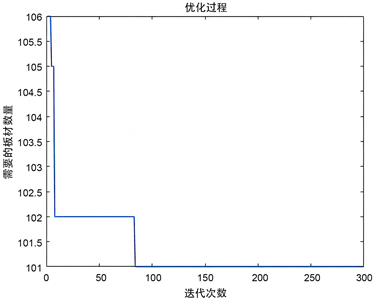
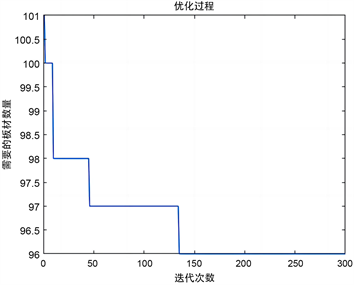
DataA1适应度函数变化图DataA2适应度函数变化图DataA3适应度函数变化图DataA4适应度函数变化图

Figure 3. Change of the appropriate function of the new layout scheme of Data A

图3. 数据A新方法排样方案适度函数变化图

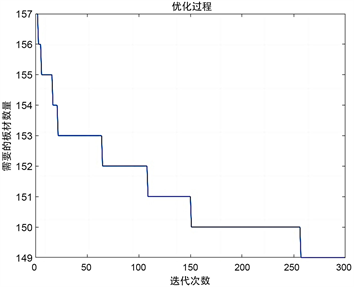
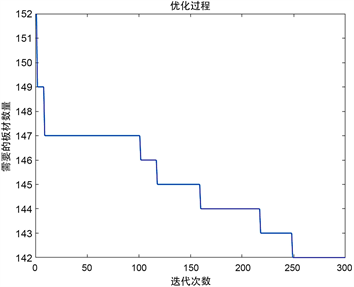
DataA1适应度函数变化图 DataA2适应度函数变化图DataA3适应度函数变化图 DataA4适应度函数变化图

Figure 4. Change of the appropriate function of the original layout scheme of Data A

图4. 数据A传统排样方案适度函数变化图

4. 结果分析

本文以A2数据为例进行结果展示分析对比，由3.3节中的两种模型求解方法可以得到以A3数据为例的切割方形件的结果。首先对本文使用的加预处理方法的切割方式进行可视化，如下图5所示：

Figure 5. DataA2 New method for laser cutting square piece track map

图5. DataA2新方法激光切割方形件轨迹图

对传统未加预处理的切割方法可视化如下图6所示。

通过对比两种方法的切割效果图(图5和图6)，可以明显得出对于相同的产品要求，本文采用的切割方法仅需要101块原材，有效利用率高达82.05%，而传统按照ID全排列的方法需要149块方形件原材料。由于新方法采用了长度和宽度相同的产品项组合成条带，再对条带进行预处理排列，使得单块方形件能切割较多的产品项。从上图5和图6的对比中可以看出，加预处理的新方法相较传统方法板材切割更均匀、密集，而传统方法则出现大片板材切割不充分，浪费较严重。因而采用新方法大大提高了激光切割方形件材料的有效利用率。并且从适应度函数图可以看出新方法只需要迭代83次即可达到最优解，而传统方法需要迭代到258次才能达到最优解。可见新方法大大减低了运行时间，可以更快的找到最优解。

Figure 6. DataA2 Traditional method for laser cutting square piece track map

图6. DataA2传统方法激光切割方形件轨迹图

利用遗传算法求解两种方法，所需的迭代次数对比如下图7所示。可看出对条带数据进行预处理排列可以大大降低遗传算法求解的迭代次数，且4组数据的迭代次数都有不同程度减少，提高了求解效率。

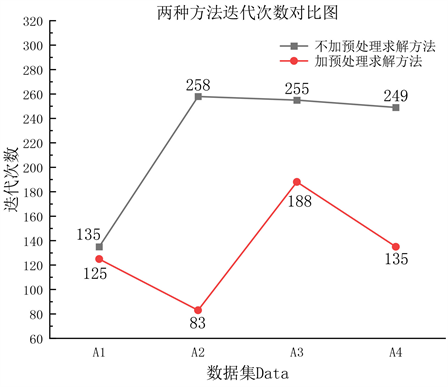
Figure 7. Comparison of iteration times of two methods

图7. 两种方法迭代次数对比图

本文通过以上两种方法计算数据集A中所有数据的有效利用率如下图8所示。

从图8中可以看出通过对条带使用预处理的方法进行排样切割，使得有效利用率相较传统方法提高了近15%，且对于产品项尺寸规格越相近的，有效利用率越高。

从另一方面板材使用数量对比图如下图9所示也可以得出本文所使用方法的优越性。

由上图9可看出，加预处理后的切割方法所需的板材数量由之前的近150块原材料下降到了近90块，大大降低了原材料的使用率，提高了材料的有效利用率。同时也降低了激光切割机的使用频率和装卸板材的次数，大大降低了生产成本。

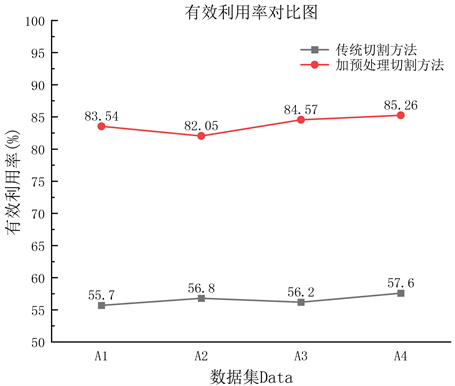
Figure 8. Comparison chart of effective utilization

图8. 有效利用率对比图

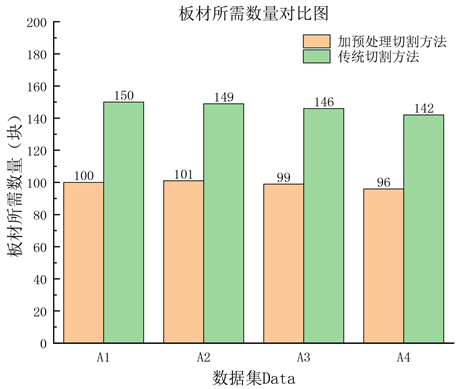
Figure 9. Comparison diagram of required quantity of plates

图9. 板材所需数量对比图

5. 结语与建议

针对三周激光切割方形件排样优化和订单组批问题，为了更好的节约原材料、提高激光切割机的使用效率、减低生产成本，本文提出的数据预处理加遗传算法模型，利用订单数据，按长度和宽度进行归类并排列成更大的产品项，最后组成条带，对其进行数据预处理并结合遗传算法求解排列方式。最后将方形加工件的排列方式可视化展现出来。相较传统id全排列方式有效利用率提高了近15%。同时大大减少了激光切割机的使用率，降低机器磨损和人工成本。充分说明本文所用的建模方法的高效性和实用性。每个加工厂都涉及到原材料的下料问题，其中方形件材料尤为突出。方形件的排样优化和订单批次值得深入研究，高效率的模型可以大大提高材料利用率和提高激光切割机的使用寿命，最终降低生产成本。