1. 引言
近年来,随着5G的发展,通信的带宽增大,但基站的能覆盖范围减小,使得覆盖同样的区域,需要的基站数量增多,另外,基站和天线的种类也变多了。侯群等采用COST231 Hata修正模型实现了无线局域网(wireless local area network, WLAN)室外覆盖网络预算分析 [1] ;丁远等将3D Uma模型与粒子群优化算法结合,实现了所选区域的5G站址规划 [2] ;谢许凯等分析了5G通信站址选择的数学模型,并采用遗传算法(genetic algorithms, GA)和免疫算法得到基站位置的最优解 [3] 。移动通信基站站址规划将直接决定城市移动通信网络质量的好坏,是城乡发展规划通信部分不可或缺的内容。
本文根据某城市某区域的现网覆盖情况,在现网的弱覆盖区域上新建基站后,解决现网的弱覆盖区域的覆盖问题。根据给定的信息中的数据,在给定区域内的2500 × 2500个点中选择站址的坐标,进行站址规划,使得弱覆盖点总业务量的90%被规划基站覆盖。给出选择的站址的坐标以及每个站址选择的基站种类 [4] 。
2. 基站的覆盖分析
对于给出2500 × 2500个点,以及需要覆盖的点的网格坐标和业务量。假设弱覆盖点是在平面上是均匀分布,可以将问题简化为几何概率大于90%的情况下,如何最大减少成本。
通过计算如图1所示的覆盖率能达到 [5] :
显然此种覆盖直接使用是不合理的,因为宏基站的使用率过高,造成资源浪费。接着考虑第二种排列方式 [6] 。已知一个宏基站的半径是30,则把边长为60的正方形网格作为一个单元去分布宏基站。区域总横坐标长度为2500,所以在x轴方向上的单元个数应该是2500 ÷ 60 = 41.67,这里取为42。所以对于原本的2500 × 2500的进行简化,简化为42 × 42的格子。下面对这些格子进行覆盖计算:
如图2(a)所示,当格子中心距离现有基站距离大于10,则将会在这个中心点处去放置宏基站,否则如图2(b)所示,不满足门限要求则这个中心点就不能被当作宏基站的放置点。挑选出中心点距离现有基站10以上的方格,然后在这些方格的中心放置宏基站。宏基站覆盖的弱覆盖点除去。这时候一个方格的四个角是弱覆盖点的集中区域。
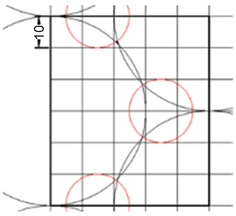
Figure 1. Schematic diagram of base station coverage
图1. 基站覆盖示意图
 (a)
(a) 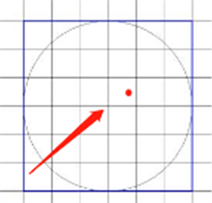 (b)
(b)
Figure 2. (a) The distance between the cell center and the existing base station is greater than 10; (b) The distance between the cell center and the existing base station is less than 10
图2. (a) 格子中心距现有基站距离大于10;(b) 格子中心距现有基站距离小于10
如图3所示,1 2 3 4四个区域有大量的未覆盖区域,而且这四个区域是中心对称图形,可以考虑把四个区域放在一起去看 [7] ,如下图4所示:
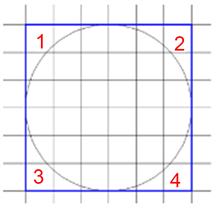
Figure 3. Schematic diagram of Acer station gap
图3. 宏基站空隙示意图
对于每一个这种四角空隙结构,需要这几个小基站去填充,把两个方法都算一遍,选用覆盖的总业务量多的方法。
3. 模型建立的预处理
3.1. 数据预处理
3.1.1. 删除业务量小于1的点(为减少计算量)
服务量小于1的弱覆盖点个数较多,但在满足覆盖率大于90%的条件下,显然没有业务量高的点重要性强。在数据预处理阶段,将业务量小于1的弱覆盖点筛选掉,能够显著减少运算量,并且对最终结果影响较小 [8] (表1,图5)。

Table 1. Proportion of weak coverage points with traffic less than 1
表1. 业务量小于1的弱覆盖点占比
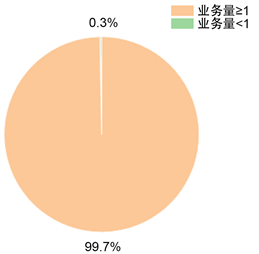
Figure 5. Proportion of weak coverage points with service volume less than 1
图5. 服务量小于1的弱覆盖点占比
3.1.2. 弱覆盖点的分布情况分析
图6将弱覆盖点数据绘制为平面气泡图,气泡大小代表弱覆盖点业务量的大小。从图中可以观察到,弱覆盖点在平面内并不是均匀分布,部分地区密集,部分地区稀疏;此外,弱覆盖点的业务量差别巨大,最大的单个弱覆盖点业务量大于4万,最小的却小于1,因此,在后续进行站址规划时,应首先覆盖业务量大的弱覆盖点,其次在覆盖业务量较小的弱覆盖点。
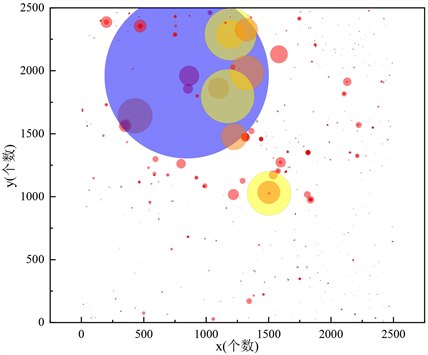
Figure 6. Plane distribution of weak coverage points
图6. 弱覆盖点的平面分布图
了解弱覆盖点业务量的分布有助于我们提出合适的站址规划初始值,对弱覆盖点的业务量进行统计分析得到上图,由频数分布直方图可知,业务量在1~10之间的弱覆盖点数量最多,且数量显著多余其他段弱覆盖点;服务量大于200的弱覆盖点数量上占总数很少(图7)。

Figure 7. Frequency distribution histogram of weak coverage point traffic
图7. 弱覆盖点业务量的频数分布直方图
通过以上对弱覆盖点数据的分析,优先覆盖业务量大的弱覆盖点,既可以保证容易达到覆盖率指标,又减少花费,这一主要思想贯穿问题的解答过程。
3.1.3. 宏/微基站的性价比分析
对比宏基站与微基站的成本与覆盖量,定义单位成本覆盖面积指标,即单位成本能够覆盖的面积越大,则覆盖均匀业务量密度的区域约划算,宏基站单位成本覆盖面积为282.7,而微基站的单位成本覆盖面积为314.0 (表2)。

Table 2. Cost performance analysis of macro/micro base station
表2. 宏/微基站的性价比分析
3.2. 模型假设与约定
1) 服务量小于1的弱覆盖点不考虑;
2) 还有信号强度与距离中心点的距离无关,假设在覆盖范围内强度不变;
3) 业务量小的点在实际场景中,将其覆盖的优先级低。
3.3. 符号说明及名词定义
60 × 60网格:面积为60 × 60网格,具体划分个数为42 × 42。
Traffic:业务量。
4. 模拟退火算法模型的建立
通过上述分析我们了解到,优先使用大覆盖范围的宏基站覆盖业务量大的弱覆盖点这一策略可以获取可靠的算法运行初始值(图8)。
为了得到平面上业务量密度分布信息,我们定义60 × 60方格内弱覆盖点的总业务量为密度指标,优先在业务量密度大的地方放置性价比更高的宏基站 [10] 。该方法实际执行中包括以下难点问题:
1) 宏基站具体位置的选则。60 × 60方格的中心可能不符合与已有基站的门限约束,如何在60 × 60方格中选择最佳宏基站位置成为主要面临的问题。
2) 已有站址的门限约束处理。容易得出,在2500 × 2500的平面上,约包含625 w个可选择点,已有站址也多达1474个,快速求解可选择点或已有站址覆盖点成为限制计算速度重要问题。
若成功解决上述难题,则可以规划微基站的数量与位置。微基站覆盖范围小,但是成本低,适合覆盖孤立但业务量大的弱覆盖点。为了找到该类弱覆盖点,我们将平面划分为长度为20 × 20的方格,查到宏基站未覆盖的但业务量大于阈值的方格,来放置微基站。此时,我们得到一组覆盖率较好的初始值。
5. 模型关键问题求解
利用模拟退火算法,改变初始布置宏基站的数量与初始布置微基站的数量,对目标函数进行优化,得到覆盖率与建设基站花费均最优的指标 [11] 。
60 × 60方格区域划分,按照长度对网格划分,划分完成后形成42 × 42个方格;对方格中弱覆盖点进行密度统计,得到下图9。
为了确定初始值,对划分好的网格中弱覆盖点业务量密度进行统计分析,其频数分布直方图如下图10所示。

Figure 8. Flow chart of base station site selection algorithm
图8. 基站站址选择算法流程图
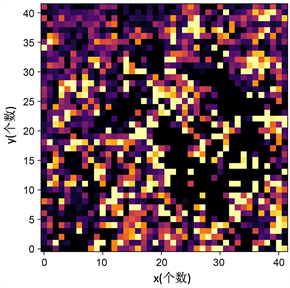
Figure 9. Distribution of traffic density in the 60 × 60 grid area
图9. 60 × 60方格区域业务量密度分布图
由图10可知,单个网格中业务量总和超过4000的网格数量较多,业务总量在500~4000之间的网格数量较少,业务总量低于100的网格数量也很多。此时,我们根据直方图的分布,设置一个初始值作为放置宏基站的阈值,即若该网格业务总量超过阈值,则试图在网格中心处放置宏基站,若网格业务总量低于阈值,则不放置宏基站 [12] 。此时我们经过计算得到了需要放置宏基站的格子集合。
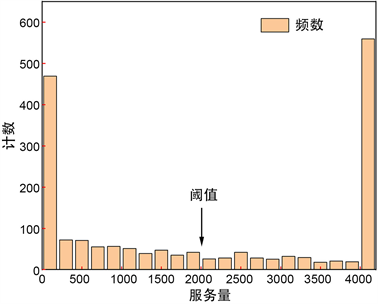
Figure 10. Histogram of frequency distribution in 60 × 60 grid
图10. 60 × 60网格频数分布直方图
关键问题的解决1:宏基站具体位置的选则。
在单个边长为60 × 60的网格中,放置宏基站并满足约束条件。首先尝试遍历网格内的弱覆盖点,若弱覆盖点距离网格中心较近,甚至弱覆盖点就是网格中心并满足门限约束条件,则用此弱覆盖点的坐标作为宏基站的放置位置 [13] 。该方法的站址选择示意图如图11所示:

Figure 11. Schematic diagram of Acer site selection algorithm
图11. 宏基站站址选择算法示意图
若未在60 × 60网格中寻找到合适的弱覆盖点作为放置坐标,则按照以下算法寻找最优安放位置,如下图12所示,按照红色箭头方向依次遍历方格内所有点,对于每一个点判断其是否满足门限约束,若满足则选择该点作为宏基站放置坐标,若不满足则判断下一点,该算法保证了宏基站最大可能覆盖全部的格子。
具体原理解释如下,初始化以(0, 0)为中心上下左右边长各为10的平面坐标区域,按照坐标距离原点位置减去坐标绝对值进行排序,得到红色箭头路径。
关键问题的解决2:已有站址的门限约束处理。
在2500 × 2500的平面上,约包含625 w个可选择点,而给出的已有站址也多达1474个,快速求解可选择点或已有站址覆盖点成为限制计算速度重要问题 [14] 。

Figure 12. Schematic diagram of optimal coordinate selection algorithm in 60 × 60 grid
图12. 60 × 60网格内最优坐标选择算法示意图
由于我们判定门限约束的条件是两点之间距离大于10则满足门限约束,因此可以理解为以一点为圆心,计算半径为10的圆覆盖整数点的个数,将一点作为原点,计算覆盖整数点的示意图如图13所示:
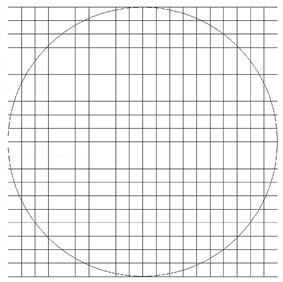
Figure 13. Schematic diagram of integer points covered by a circle with radius 10
图13. 半径为10的圆覆盖的整数点示意图
目前已知坐标在原点处的圆覆盖整数点集合,若想知道任意坐标半径为10的圆覆盖整数坐标点集合,仅需要对我们求解的第一个集合进行坐标变换即可。
关键问题的解决3:宏基站与微基站的最佳覆盖搭配方式。
利用宏基站与微基站搭配,得到最佳的覆盖率是确定宏基站与微基站数量的关键一环。在总业务量较高的地区,我们需要较高的覆盖率,在总业务量较低的地区,可以一定程度上减少覆盖率(表3,图14)。
通过模拟退火算法得到了宏基站与微基站的最佳数量搭配 [15] ,结合上述宏基站与微基站的最佳覆盖搭配方式,覆盖率超过90.1%,满足要求(图15)。
图15中,黑点代表弱覆盖点,蓝色圆圈代表微基站,红色圆圈代表宏基站。可以看出弱覆盖点得到了很好的覆盖(表4,表5,图16)。

Table 3. Base station type and number planning table (part)
表3. 基站类型及数量规划表(部分)
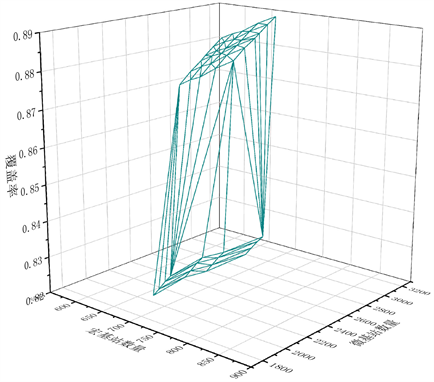
Figure 14. Effect of simulated annealing algorithm to optimize the number of base stations
图14. 模拟退火算法优化基站数量效果图

Figure 15. Schematic diagram of site planning for weak coverage points
图15. 弱覆盖点的站址规划示意图

Table 4. Summary of planned base stations
表4. 规划基站汇总表

Table 5. Uncovered points are listed in reverse order by traffic volume
表5. 未覆盖点按业务量逆序排列
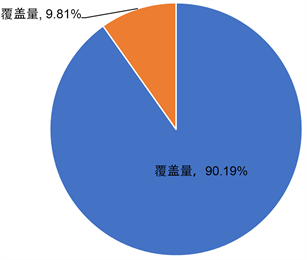
Figure 16. Coverage diagram of the planned site
图16. 规划站址覆盖情况图
在当前基站规划选址情况下,覆盖量约为90.19%,大于题目给出的90%,符合要求,且成为为8032。由上表可得,未覆盖点中最大业务量为455.40,说明业务量大于455.40的弱覆盖点都被规划基站覆盖。
6. 结论
把2500 × 2500个数据点划分成42 × 42个边长为60的方形格子,按照格子内的业务量的高低去分配基站,通过设置宏微基站阈值,利用模拟退火算法,改变初始布置宏基站的数量与初始布置微基站的数量,对目标函数进行优化,得到覆盖率与建设基站花费均最优的指标。通过模拟退火算法得到了宏基站与微基站的最佳数量搭配,宏基站578个,微基站2252个,总花费8032,覆盖率超过90.1%,可以满足要求。