1. 引言
近年来,低维系统中的电子关联和超导性深受广泛研究 [1] [2] [3] ,关联作用在一维半满填充下会对体系量子特性产生很大的影响。哈伯德模型被公认为是处理电子关联效应的原型,在位排斥相互作用(U > 0)对umklapp散射过程有着至关重要的影响,导致一维电子系统在半填充时成为绝缘体。哈伯德模型是人们理解强相关系统的基础,尽管如此,它的标准哈密顿量中势能项只包含在同一位置自旋相反二个电子之间的相互作用,如果扩展到包括长程相互作用,预计将改变系统的量子行为。强关联电子系统一直以来因其拥有的丰富相图和带来的独特材料性质备受研究者们的青睐 [4] [5] 。近年来,一些关于具有强偶极矩的分子和原子的超冷费米气体的实验 [6] [7] [8] 从全新的角度揭示了强关联系统的特殊性质。与以往的强关联电子系统不同的是,实验者们通过一些特殊实验手段 [9] [10] 探测到了不能被传统费米液体理论所解释的相互作用,例如长程耦合和多体耦合 [11] [12] 。对此类材料的实验研究以及相关的理论研究将加深我们对强关联电子系统的理解,拓宽材料物理的研究界限。实验中三体相互作用存在的直接证据已在光晶格或磁光阱中的Rb87里德堡原子里观察到 [13] 。实际上,作为非常规相互作用的代表,研究者们热衷于对三体相互作用的探究,Johnson等人 [14] 的研究表明,在三维光学晶格中处于最低振动状态的原子的二体碰撞可以产生有效的三体相互作用。Büchler等人 [15] 发现,由微波场驱动的极性分子会产生强烈的三体相互作用。Hammer等人 [16] 也证明了三体相互作用在多体系统中存在的可能性和合理性。
实际上,关于三体相互作用的一维理论很早就有相关报道。一方面,一维模型的理论研究更加理想化,另一方面,一维模型的物理性质也更加特殊。作为一维强关联电子系统的典型模型,一维扩展Hubbard模型(t-U-V)被广泛用于各类模型的搭建。t-U-V模型的哈密顿量为:
(1)
式中,
为电子的产生(湮灭)算符,
为数密度算符。t-U-V模型已得到了广泛的研究,在半满情况下,强耦合 [17] 和弱耦合 [18] 理论都表明,该模型在U = 2V附近存在CDW-SDW绝缘相变。在t-U-V模型的基础上,区别于非对角三体相互作用 [19] [20] ,我们增加对角化三体相互作用 [21] ,其哈密顿量可表示为:
我们得到受三体相互作用影响的一维扩展Hubbard模型:
(2)
它是标准对角二体相互作用U和V的推广,然而它并不直接来自两体库仑排斥相互作用,而是反映了多体相互作用。与U和V项不同的是,P项在物理中可以是排斥作用,也可以是吸引作用。该模型满足自旋SU (2)对称性和电荷U (1)对称性,它的相图是二体相互作用和三体相互作用之间竞争的结果。在有效场论中,三体相互作用和更多体相互作用的介入,在强相互作用的量子系统中尤为突出。三体相互作用在量子力学和量子多体问题中发挥着重要作用。在凝聚态物理学中,各种三体相互作用被增加到已有的二体模型中,被认为是获得新相的新颖尝试,尽管多数情况中,在重整化群意义下,它们是无关量。通常假设多体系统的物理主要是考虑两体相互作用来描述,但这些被忽略的项不能总被认为与所有系统的物理无关。对于费米子系统,多数研究的三体耦合是关联跃迁项,这是半填充下出现Haldane电荷序的一个物理原因。对于玻色子系统,已证明三体耦合能够导致超导关联和电荷调制的超固体相。不仅如此,目前冷原子和冷分子系统的实验进展允许人们通过可控方式研究一维晶格系统中多体作用的影响。一维光晶格中多种超冷气体和非零偶极矩的实验为二阶以上的多体相互作用开辟了道路,在磁光阱中的冷Rb-Rydberg原子中也观察到了三体相互作用。目前缺乏对角三体相互作用对扩展哈伯德模型相图影响的详尽描述,所考虑的模型(2)正致力于这个问题的研究。此外,哈密顿量(2)可以为超导态的实现提供一种理论方案。众所周知,相互作用是相互关联的多体量子相位的核心,特别是高阶多体相互作用可能产生新的量子相。目前,由微波场驱动的光学晶格中的极性分子自然产生了具有强最近邻相互作用的哈伯德模型。所有这些都促使我们考虑哈伯德模型的进一步推广,其中就包括最近相邻的粒子密度–密度耦合(P)为特征的高阶相互作用。研究表明,吸引P相互作用在U、V排斥作用下能够导致半填充时的超导基态。对于
,P耦合导致SS-CDW相变,而对于
,P耦合驱动Mott-TS相变。
2. 玻色化和重整化群理论
玻色化 [22] 和重整化群理论 [23] [24] 给一维强关联电子系统的弱耦合分析提供了强有力的理论支持,是分析此类模型相图的最有效的解析方法。
2.1. 玻色化
我们首先将哈密顿量中的产生(湮灭)算符在低能条件下展开:
(3)
再代入玻色化公式:
(4)
式中,
和
是一对共轭玻色场。经过一系列复杂的数学计算 [25] ,哈密顿量可以写成如下自旋–电荷分离的形式:
(5)
其中,
(6)
(7)
(8)
(9)
(10)
方程(5)表示Sine-Gordon模型 [26] ,g1~4 [27] 代表了电子之间的四种散射关系,
分别表示散射的电子的自旋方向相反和相同。将哈密顿量改写成上述形式的好处是,描述电荷激发和自旋激发的电荷场和自旋场是分离的,这样就能清楚知道每种激发对相图的贡献。
但是,Sine-Gordon模型是基于二体相互作用的理论,三体相互作用项不能直接计算得到上述形式,需要经过约化,约化方法可以参考 [28] ,或文献 [29] [30] 的算符乘积展开,我们选择后者。经过约化和计算,我们得到耦合常数:
(11)
(12)
(13)
2.2. 重整化群理论
在重整化群理论中,有效耦合常数与标度长度 有关。根据一环微扰重整化群方程:
(14)
(15)
和流向图 [31] ,由裸耦合常数之间的关系得到如下不同性质的区域:
1) 当
时,系统处于弱耦合区域。随着重整化的进行,
,有效质量
,模型退化为高斯模型
。这表明电荷(自旋)激发是无能隙的,系统由标量场描述,关联函数相应呈幂律形式衰减:
(16)
2) 当
时,系统处于强耦合区域。根据
的初始值,有效质量
,电荷(自
旋)激发是有能隙的。相场的真空期望值为:
(17)
3. 相图
我们现在可以得到一维扩展Hubbard模型在三体相互作用影响下的基态相图,如图1(a)和图1(b)所示。为了确定一个区域内的主导关联态,我们采用了表1中玻色化形式的序参量 [32] :
首先,当
时,有效质量
,电荷激发无能隙。如果
,那么有
且gs < 0,此时自旋场真空期望值
,CDW、BOW和SS相的序参量都有可能处于最大值,但是SS相的关联
衰减慢于另外两相,因此系统处于单重超导(SS)态。如果
,那么有
,此时电荷激发和自旋激发都是无能隙的,所有的绝缘相都被抑制,系统处于三重超导(TS)态。
其次,当
时,有效质量mc ≠ 0,电荷激发有能隙。如果
,那么有
且
,
,此时电荷场和自旋场的真空期望值分别为
、
,容易算出CDW相的序参量取最大值,系统处于电荷密度波(CDW)态。如果
,那么有
且
,
,自旋激发是无能隙的,电荷场的真空期望值
,BOW相和SDW相的序参量都可能取最大值,但是SDW相的关联衰减慢于BOW相,因此系统处于自旋密度波(SDW)态。
 (a) P > 0
(a) P > 0 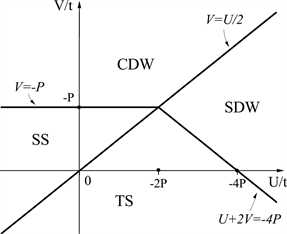 (b) P < 0
(b) P < 0
Figure 1. The phase diagram of t-U-V-P model
图1. t-U-V-P模型的基态相图
4. 量子仿真
为了进一步探究三体相互作用的影响,我们再进行量子仿真。量子仿真技术主要分为两类,一类是数值量子仿真 [33] ,另一类是类比量子仿真 [34] ,我们选择了更加直接的数值量子仿真。数值量子仿真方法也有多种选择,如适用于自旋系统的Suzuki Tkotter方案 [35] [36] [37] [38] 和Handscomb [39] 方案,还有适用于相互作用系统的世界线 [40] 和行列式 [41] [42] [43] 方法。我们采用世界线方案,相较于其他方案,该方案更便于直接考虑各种相互作用之间的竞争。首先,我们再现了文献 [44] 中t-U-V模型的表现,在t = 1、U = 4、时间步长
(本文默认t = 1,
)的条件下,经过10,000次循环计算,每5次
循环统计一次参数,得到了CDW序参量的绝对值
在V从1至3.5以步长0.1增加
时的增长过程,得到图2,仿真结果符合t-U-V模型在
发生SDW-CDW绝缘相变的理论预测。

Figure 2. The rise of
in the t-U-V model
图2. t-U-V模型
的增长
我们再考虑三体作用与二体作用的竞争,在相同设定下(假定
)研究了CDW相的边界,即
和
两条相变线。如图3,t = 1,U从−2到6以0.1的步长增长,V也在合适的范围内以0.1的步长增长,每个像素代表一次固定参数的仿真,每次仿真的循环计算次数达到10,000次,统计参数的样本达到1000个,像素的颜色代表了该固定参数下CDW序参量绝对值
的统计平均值的大小,从紫色到红色逐渐增加,虚线代表理论预测的相变线(
,
)。

Figure 3. The distribution of
in t-U-V-P model
图3. t-U-V-P模型
的统计
图3给出了一些有价值的结果。首先,在三体相互作用项的影响下,相变线附近
的改变并不迅速,如图4所示为例(t = 1, U =0, P = −2),这代表着相变可能是连续相变,理论预测的相变线附近可能有其他关联态的存在,系统的相分布并不像理论那样单一。另外,相较于U变化的两端,四相交汇点附近的仿真结果与理论预测的偏差更大,与两端形成一个较为平滑的曲线,这代表着四相交汇点附近的情况甚至更加复杂。这种偏差可能是由三体相互作用的约化导致的,另一个原因是本文所用的理论是一个微扰理论。尽管如此,理论分析还是在一定程度上揭示了t-U-V-P模型的相区分布,附录中附图1展示了各种参数下展现的相区特征。

Figure 4. The rise of
in the t-U-V-P model
图4. t-U-V-P模型
的增长
5. 结论
本文在一维t-U-V模型的基础上,加入了对角三体相互作用项,得到t-U-V-P模型。我们运用玻色化和重整化群理论,研究了三体相互作用对t-U-V模型基态相图的影响。理论研究发现,相变线
将整个区域分为4个相区,当
时,电荷激发无能隙,自旋场真空期望值
,系统处于SS态;当
时,电荷和自旋激发都有能隙,系统处于CDW绝缘态;当
时,电荷和自旋激发都无能隙,所有的绝缘相都被抑制,系统处于TS态;当
时,电荷激发有能隙,自旋激发无能隙,系统处于SDW态。随后,我们用数值量子仿真研究了t-U-V-P模型,发现尽管上述理论在一定程度上成功预测了该模型的相区分布,但是并未完全揭示该模型相变的性质,对CDW相变线附近的序参量统计发现,相关相变可能是连续相变,且存在着更加复杂的关联态。
附录
图片从仿真过程中截取而来,其中黑色的上半圆代表格点被自旋向上的电子占据,白色的下半圆代表格点被自旋向下的电子占据,灰色的圆代表双占据,空白代表没有电子,每行表示一个可能的中间态,从下至上为世界线方向,详情见 [40] 。
 (a) CDW: U = 0, V = 0, P = −2
(a) CDW: U = 0, V = 0, P = −2  (b) SDW: U =7, V = 3, P = −2
(b) SDW: U =7, V = 3, P = −2  (c) SS: U = −2, V = 1, P = −2
(c) SS: U = −2, V = 1, P = −2  (d) TS: U = 4, V = 0, P = −2
(d) TS: U = 4, V = 0, P = −2
Figure S1. The characteristics of different states
附图1. 不同相区的特征
NOTES
*通讯作者。