1. 引言
少齿差行星齿轮减速器的优点相比传统齿轮减速器要明显的多,具有高速、重载、速比大、运行平稳、精密等特点 [1] 。
目前,关于少齿差行星齿轮减速器的研究,有部分学者取得一定的进展。摆线齿廓应用在针齿传动中比较成熟,但对于内、外摆线齿廓同时与针齿的圆形齿廓啮合传动的研究较少,且由于受力的问题,销轴输出机构容易损坏,是针齿传动中比较脆弱的环节,影响减速器的使用寿命 [2] [3] 。而NN型少齿差传动使用双联行星轮,具有传动比大,结构简单等优势,但内齿轮数减小、齿数差少时,双联齿轮与同时啮合的内、外齿轮就会产生齿形重叠干涉,对于传动的设计比较复杂,需要一系列圆柱销组成针排齿轮与内、外摆线轮实现啮合传动 [4] [5] 。
本文的新型针排齿轮传动具有下面的特点,将内、外摆线齿廓与NN型少齿差传动结合,在保留传动比相对较大,传动精度相对较高的同时,摆线轮输出不再需要单独的输出机构,且避免了NN少齿差传动设计时齿形重叠干涉。以新型针排齿轮减速器为对象,研究新型少齿差行星齿轮减速器结构的固有频率和动载特性,为工程人员进行针排齿轮传动和减速器结构设计提供重要参考。
2. 新型针排齿轮减速器传动原理
新型针排齿轮传动采用NN型少齿差方式,将针齿销组成的针排齿轮做为双联齿轮,由内摆线齿轮4、外摆线齿轮1、圆柱销和销环固定架组成的针排齿轮2~3组成,针排齿轮与内、外摆线齿轮同时啮合,共同完成减速任务,其机构简图如图1所示。
通过新型针排齿轮传动的结构简图,当摆线内齿轮4固定时,机构的自由度为F = 1,该机构具体唯一确定的运动,输入轴为偏心轴,针排针轮为行星轮,摆线外齿轮直接进行动力输出。电机带动偏心轴做定轴转动时,偏心轴将带动针排齿轮做公转,此时由于针排齿轮与内、外摆线齿轮啮合,摆线内齿轮迫使针排齿轮产生一个自转运动,再通过与内摆线齿轮啮合,将动力反馈给摆线内齿轮实现动力输出。
3. 减速器运动学和动力学仿真分析
通过运动学和动力学仿真来研究新型针排齿轮减速器结构系统的传动比和啮合力。针对传动比的分析可以验证新型针排齿轮传动的可行性和虚拟样机建立的正确性。针对啮合力的分析可以计算出传动时实际参与啮合的齿数。
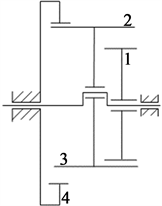
Figure 1. Schematic diagram of pin gear transmission structure
图1. 针齿齿轮传动结构简图
将新型针排齿轮减速器简化后的三维模型导入ADAMS中 [6] ,将模型定义为各向同性、密度均匀的弹性体,各主要零件的材料属性设置如表1所示。简化后的新型针排齿轮减速器模型有四个零件,为方便后续操作和方便观察,将新型针排齿轮设置为红色,输入偏心轴为绿色,输出外摆线轮为蓝色,内摆线轮为白色,则虚拟样机的模型如下图2所示。

Table 1. Reducer material attribute setting table
表1. 减速器材料属性设置表
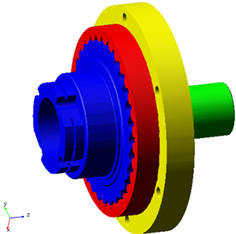
Figure 2. Simplified virtual prototype model of new type pinwheel reducer
图2. 简化后新型针排齿轮减速器虚拟样机模型
此时ADAMS中的新型针排齿轮减速器零部件之间还没有关联,需要对减速器模型进行相关的运动副和约束添加,完成新型针排齿轮减速器的虚拟样机。整个针排齿轮减速器虚拟样机相关运动副和约束的设置如下表2所示。
利用虚拟样机对新型针排齿轮减速器进行动力学仿真时,要想得到针排齿轮与内、外摆线轮的啮合特性较好的仿真结果,就要对其涉及到的接触进行详细设置。对于接触物体间的摩擦力选用库仑摩擦类型,进行运动学分析时可以不忽略摩擦,但进行动力学仿真分析时,需要考虑接触受到的静摩擦和动摩擦,一般来说有润滑时,取静摩擦系数0.08,动摩擦系数0.05,没有润滑时,取静摩擦系数为0.15,动摩擦系数为0.1 [7] 。

Table 2. Relevant kinematic pairs and constraint settings
表2. 相关运动副与约束设置
在虚拟样机进行运动学仿真之前,对已经约束好的输入偏心轴施加一个恒定的转速驱动,为了使新型针排齿轮减速器的虚拟样机能够平稳的工作,可以利用adams中的函数STEP来设置输入转速 [8] ,为降低虚拟样机在仿真一开始由于转速过快导致各接触产生冲击对仿真精度产生影响,从0~0.1 s的时间内,电机平稳启动,从静止加速到2400 (相当于电机转速400 r/min),使用STEP的阶跃函数完成。
设置完上面的参数后,利用adams对建立的新型针排齿轮减速器进行运动学仿真,设置分析时的时长为1 s,选择分析步数为0.005,进行运动学求解,并输出仿真结果 [9] 。其中,新型针排齿轮减速器虚拟样机外摆线轮输出轴的角速度变化曲线如图3所示。
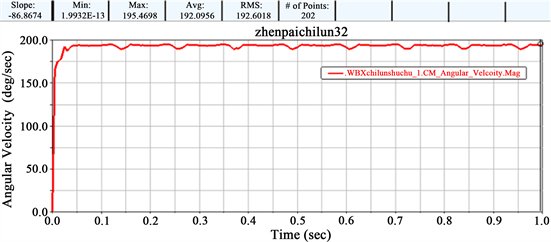
Figure 3. Epicycloid output shaft angular velocity curve
图3. 外摆线输出轴角速度曲线
输入轴为逆时针方向转动,且稳定时的转速为3000,从图中可以看出,外摆线输出轴的角速度为正值,符合针排齿轮传动的特点,且角速度在平均值192.0956上下波动,因此通过仿真而得到的新型针排齿轮减速器的总传动比为:
将虚拟样机仿真而计算出的减速比与理论计算出的减速比i = 31相比,其误差为0.75%,在误差允许的范围内,外摆线轮输出轴的仿真结果不仅验证了之前的传动理论分析,也验证了所建立的新型针排齿轮减速器虚拟样机的正确性。
对于新型针排齿轮减速器来说,最核心的部分就是针排齿轮圆柱销和内、外摆线轮啮合时的状况,因此对于传动中圆柱销和内、外摆线轮的啮合力的仿真很重要。可选定400 r/min-80 N∙m、800 r/min-80 N∙m、1200 r/min-80 N∙m、800 r/min-50 N∙m、800 r/min-120 N∙m几种典型状况,得到减速器内、外摆线轮啮合力如图4所示。
将对圆柱销与内、外摆线轮啮合力理论计算的结果与虚拟样机仿真出来的仿真数值进行对比,如下表3所示。

Table 3. Calculation and simulation values of maximum meshing force of inner and outer cycloid gears
表3. 内、外摆线轮最大啮合力计算值与仿真值
通过上面的分析,当新型针排齿轮减速器在合适的工况下,理论计算的最大啮合力和虚拟样机仿真的结果误差很小,在实际的针排齿轮传动中,输入轴的转速会影响内、外摆线轮和圆柱销之间的最大啮合力,且随着转速的升高,啮合力的波动也随之增大,当转速超过额定转速时,最大啮合力的波动会对传动稳定造成一定影响;外摆线轮输出轴阻矩直接影响啮合力的最大值,但对其最大啮合力的波动性影响较小。
4. 减速器动载特性分析
利用建立的虚拟样机,以针排齿轮行星传动中圆柱销与内、外摆线轮的啮合力为目标,采用控制变量法,单独考察减速器设计参数对减速器动载特性的影响。
使用建立的新型针排齿轮减速器的虚拟样机参数为基础进行啮合力研究 [10] ,当Rz = 41mm,rz = 3 mm,Za =31,Zb = 32,Zc = 33,短幅系数K1 = 0.7805,偏心距A此时为1 mm,在保证不跟切且短幅系数小于1的情况下,保持其他参数不变,取偏心距A = 0.5~1.2 mm,每隔0.1 mm取一个值,则对应的内、外摆线轮的短幅系数依次为0.3902、0.4683、0.5463、0.6244、0.7024、0.7805、0.8585、0.9366。利用建立的新型针排齿轮减速器虚拟样机进行动力学仿真,设置输入转速为800 r/min,输出轴阻矩为80 N∙m,下面分析使用同样的条件,得到结果为不同偏心距(不同短幅系数)下圆柱销与内、外摆线轮的最大啮合力,利用matlab软件中的曲线拟合功能将得到的啮合力数据进行拟合,得到圆柱销与内、外摆线轮的啮合力随偏心距的变化关系图,如下图5所示。
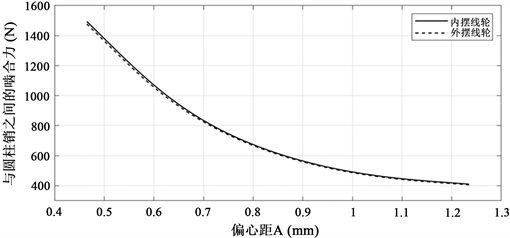
Figure 5. Variation of meshing force between cylindrical pin and inner and outer cycloid gears with eccentricity
图5. 圆柱销与内、外摆线轮啮合力随偏心距变化
由上图可以看出,当偏心距相同时,外摆线轮与圆柱销之间的啮合力始终略小于内摆线轮与圆柱销之间的啮合力,当偏心距增大时,内、外摆线轮与圆柱销之间的啮合力变化趋势一致,偏心距从0.4到0.8 (短幅系数K1从0.39~0.62)时,其啮合力减小且变化较快,偏心距大于0.8 (K1大于0.62)时,其啮合力同样减小,但变化的比较平缓。在针排齿轮传动其他参数保持不变时,增大偏心距,可以减小圆柱销与内、外摆线轮之间的啮合力和压力角,但由于偏心距的增大会使压力角变化率增大,使得传力不稳定,因此合理的偏心距(短幅系数)可以保证针排齿轮传动啮合力相对较小,且传动过程平稳,一般情况下短幅系数K1位于0.6~0.85之间时对于优化针排齿轮传动减速器的传动性能尤为关键。
圆柱销分布圆半径Rz决定针排齿轮的径向尺寸,针排齿轮的大小又影响针排齿轮传动减速器的外形尺寸,因此将其他参数保持不变,研究圆柱销分布圆半径Rz对圆柱销与内、外摆线轮啮合力的影响。在齿廓不产生跟切及K1小于1时,令圆柱销分布圆半径Rz大于35 mm而小于51 mm,每间隔2 mm取值,并保证其他的参数rz =3 mm,Za =31,Zb = 32,Zc = 33保持不变。由于圆柱销分布圆半径的变化,其内、外摆线轮的短幅系数从小到大依次变为0.9143、0.8649、0.8205、0.7442、0.7111、0.7805、0.6809、0.6531、0.6275。利用针排齿轮传动减速器的虚拟样机进行仿真,得到如图6所示的圆柱销与内、外摆线轮啮合力随圆柱销分布圆半径的变化趋势图。
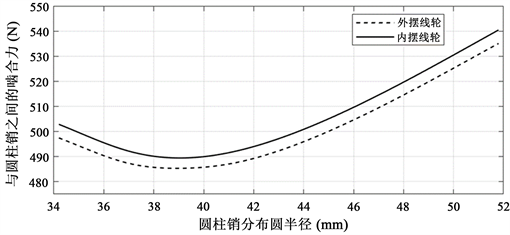
Figure 6. Change of meshing force between cylindrical pin and inner and outer cycloid gears with radius of cylindrical pin distribution circle
图6. 圆柱销与内、外摆线轮啮合力随圆柱销分布圆半径变化
由图6可以看出,当圆柱销分布圆半径Rz相同时,外摆线轮与圆柱销之间的啮合力始终略小于内摆线轮与圆柱销之间的啮合力,当圆柱销分布圆半径Rz从35 mm增加到51 mm时,内、外摆线轮与圆柱销之间的啮合力变化趋势一致,圆柱销与内、外摆线轮啮合力逐渐减小,当圆柱销分布圆半径在38 mm至40 mm时,它们之间的啮合力降低至最小值,且啮合力随着圆柱销分布圆半径的增加几乎没产生变化,当圆柱销分布圆半径从40 mm开始增加时,它们之间的啮合力开始增加,但增加的速率很缓慢,整个变化周期,啮合力最大值与啮合力最小值相差较小,因此对圆柱销与内、外摆线轮啮合力影响较小。在针排齿轮传动其他参数保持不变,内、外摆线轮短幅系数K1保持在0.6~0.8之间时,圆柱销分布圆半径对于针排齿轮传动减速器的压力角影响较大,但对圆柱销与内、外摆线轮啮合力影响较小,当圆柱销分布圆半径增大时,内、外摆线轮的压力角增大,会使传动不平稳,受力条件减弱,但此时的圆柱销与内、外摆线轮啮合力大小不一定处于相对较小,因此,为了优化出传动性能较好的针排齿传动轮减速器,可以以压力角合理的范围和啮合力的大小为优化目标,确定圆柱销分布圆的半径,为优化减速器传动性能提供依据。
研究圆柱销的半径rz对圆柱销与内、外摆线轮啮合力的影响时,由于圆柱销半径rz是关系到内、外摆线齿廓不产生跟切的主要参数,确保圆柱销半径在合理的范围进行研究,令圆柱销半径rz大于2.5 mm而小于4 mm,每间隔0.2 mm取值,由于圆柱销半径对于内、外摆线轮的短幅系数影响,因此短幅系数在分析过程中保持K1 = 0.7805,并保证其他的参数Rz = 41 mm,Za =31,Zb = 32,Zc = 33保持不变。利用针排齿轮传动减速器的虚拟样机进行仿真,得到如图7所示的圆柱销与内、外摆线轮啮合力随圆柱销半径变化趋势。

Figure 7. Change of meshing force between cylindrical pin and inner and outer cycloid gears with radius of cylindrical pin circle
图7. 圆柱销与内、外摆线轮啮合力随圆柱销半径变化
由图7可知,圆柱销半径rz相同时,外摆线轮与圆柱销之间的啮合力始终略小于内摆线轮与圆柱销之间的啮合力,当圆柱销半径rz从2.4 mm增加到4.2 mm时,内、外摆线轮与圆柱销之间的啮合力变化趋势一致,圆柱销与内、外摆线轮啮合力逐渐增大,但啮合力幅值变化不大,几乎可以忽略,圆柱销半径的增大会使内、外摆线轮与圆柱销之间的啮合刚度增大,虽然啮合力略微增大,结合第三章圆柱销半径对内、外摆线轮压力角的影响,可以得出下面的结论。
在针排齿轮其他参数确定的情况下,增大圆柱销半径rz,会使圆柱销与内、外摆线轮啮合力在很小的范围内增加,增大圆柱销半径可以降低外摆线轮压力角,但对于内摆线轮压力角是升高的,同时圆柱销半径对压力角的影响也是很小的,因此,圆柱销半径对于齿轮的动载特性影响是三个参数里面最小的,其主要影响针排齿轮传动中齿廓是否发生跟切和尖点现象 [11] ,因此为了针排齿轮传动减速器的传动性能,需要选择适当的圆柱销半径。
5. 减速器有限元模态分析
通过有限元模态分析法来研究新型针排齿轮减速器主要结构的固有振动特性,包括固有频率与模态振型。然后计算出此针排齿轮减速器齿轮副和偏心轴产生的激励频率,通过对比确保传动时产生的内部激励频率不会对传动造成较大的影响。
将整个减速器的针排齿轮传动系统作为研究主体,下面对针排齿轮产生的回转频率和圆柱销与内、外摆线齿轮产生的啮合频率进行相关的计算 [12] 。根据相关的文献资料,齿轮副的回转频率计算公式为
,其中n为转速;
为齿轮的啮合振动频率计算公式,其中n为齿轮的转速,z为齿轮的齿数。根据计算得到的此针排齿轮减速器的主要零件的转速及产生的激励频率如下表4所示。

Table 4. Speed and excitation frequency of main components of transmission system
表4. 传动系统主要部件的转速及激励频率
为了更加准确地利用有限元软件分析出针排齿轮传动系统的固有特性,按照实际的装配过程对针排齿轮传动系统进行约束,由于利用有限元进行模态分析时,其接触设置会被自动忽略,因此在导入有限元分析软件时,确保圆柱销与内、外摆线轮处于啮合状态,使得结果更加准确。
将针排齿轮传动系统的各个零件定义为相同性质,密度均匀的弹性体,按照零件对应的材料设置材料参数,完成接触和约束的设置,划分好网格然后进行求解。其中网格划分影响求解的精度,对比不同的网格精度计算的结果,当结果满足网格无关时,其求解出相对精确的固有频率和相应的振型图。
对外摆线轮固定约束,进行约束模态分析,不同网格精度与一阶固有频率的关系如下表5所示。

Table 5. First-order natural frequency values corresponding to grid density
表5. 网格密度对应的一阶固有频率数值
由表5可知,网格密度会对模态分析结果产生影响,随着网格密度的增大,其计算出的固有频率趋于收敛,得到的传动系统的一阶固有频率大约为18,273 Hz。
取针排齿轮传动系统的前六阶固有频率,约束模态分析出的固有频率数值如下表6所示。

Table 6. Natural frequency value of needle gear transmission system
表6. 针排齿轮传动系统固有频率数值
新型针排齿轮减速器的传动系统第一阶至六阶的固有频率及对应的模态振型如图8所示。
通过新型针排齿轮减速器传动系统的约束模态分析,分析得到的模态振型图,可以发现,新型针排齿轮减速器传动系统可能发生的谐振位置主要位于内摆线轮的摆线轮齿部分、针排齿轮以及外摆线轮的主体,其中内摆线轮的轮齿部分会引发发生弯曲和扭转,针排齿轮主要朝着齿厚的方向扭转,外摆线轮也产生齿厚方向的扭转。但其固有频率远大于新型针排齿轮减速器传动系统自身产生的内部激励频率,就算输入的转速增加到3000 r/min,针排齿轮传动系统产生的内部激励频率仍然远小于系统的固有频率,因此,此针排齿轮传动系统具有良好的结构特征,不会发生共振现象。
6. 总结
本文将内、外摆线齿廓运用到NN型少齿差行星齿轮传动领域,建立新型针排齿轮减速器虚拟样机,通过动载特性研究及有限元分析,得出如下结论:
1) 对减速器简化模型进行运动学仿真,验证所提出的针排齿轮减速器方案的可行性和所建立样机的正确性;对减速器进行动力学仿真,分析不同转速和阻矩对于针排齿轮传动啮合力的影响;
2) 对新型针排齿轮减速器的动载特性分析,研究了偏心距、圆柱销分布圆半径和圆柱销半径对传动的影响;
3) 对针排齿轮传动系统进行模态分析,得到前六阶的固有频率和振型图,并通过相关的计算公式求出针排齿轮传动系统的内部激励频率,结果表明该减速器结构具有良好的结构特征。