1. 引言
分子力的本质是四种基本相互作用之一的电磁相互作用,分子之间通过分子势场发生作用,其作用规律很复杂。由于分子力的复杂性,使得分子势能函数更为复杂。
分子力和分子势能函数一直都是原子分子物理学十分重要的研究方向 [1] - [10] 。分子力和分子势能函数的研究必然涉及分子内部电子和核运动电子与电子之间、电子与核之间、核与核之间的相互作用行为。
从1920年代起的近一个世纪以来,进行研究的学者们先后提出过很多种分子势能函数模型。其中,最为典型的有Kratzer势函数、Lennard-Jones势函数、Morse势函数、Hulburt and Hischeflder势函数Rydberg势函数和Murrell-Sorbie势函数、HMS势函数、TT势函数、赝高斯势函数等十几种模型。但是,这些都是基于双原子分子结构提出的分子势能函数模型 [11] ,总体比较复杂。
关于分子力和分子势能的基础研究,可以通过构建分子简化模型,根据经典电磁理论建立比较简单明了的分子力函数和相对应的分子势能函数,并用mathematica软件计算模拟出相应函数图线。
本文的研究仅以两个非极性单原子分子的相互作用予以说明,且认为这两个相互作用的分子所处的空间为真空态,有关函数表达式中各个物理量的单位均为国际制单位。
2. 分子模型的简化
分子由原子构成,原子由原子核和核外电子构成。每一个分子都有复杂的立体结构,核外电子绕原子核旋转形成复杂的电子云。为了便于简单明了的基础研究和表述,这里避开分子结构和电子云的复杂性,对分子模型作几点简化。
1) 分子是柔性(非刚性)的理想弹性球体,孤立存在时为非极性分子。
2) 核外电子在相对稳定的圆形轨道上绕原子核旋转,且电子无自旋,也不考虑原子跃迁的影响。
3) 稳定作用的两个分子的核外电子绕核旋转的方向相同,它们的轨道平面相互平行且垂直两分子的连线并关于两分子的连线对称。
4) 每个分子的核内正电荷中心与该分子的相对位置不变。
3. 分子极化
同一空间若同时存在两个或多个分子,分子间的距离在各个分子之间能够发生相互作用范围的某一定区间时,各个分子都将会不同程度地被极化,形成极性分子。分子间距离越小,极化程度越明显。
如图1所示是两个距离很近的分子被极化的一种模型,由于极化使得两分子的负电荷中心增大。其中的虚线圆为电子绕核运动的轨道,轨道中心不再是原子核(大圆点)而是负电荷等效中心(小圆点),这主要是原子核和分子电流共同作用的结果。
设这两个分子“1”和“2”的核内正电荷分别为
、
,核外负电荷分别为
、
。当这两分子之间的距离r为某一值时,令它们各自的正、负电荷中心的距离即极化距离分别为
、
。
通过用mathematica软件结合本文下述这一极化模型的分子力函数和氦分子实例数据进行模拟研究,认为极化距离
(两分子相同时
,下同)是关于分子间距离
的单调递减函数。一般地
(1)
其中,的
表示分子半径,n是与分子种类有关的待定常数,从某种角度上跟极化距离
有相同的意义,都能反映分子的极化程度。
4. 分子力函数
根据经典电磁理论可以认为:分子之间的相互作用包括原子核与原子核之间和原子核与核外电子之间以及核外电子与核外电子之间的库仑力作用,还包括核外电子绕原子核旋转形成的分子电流之间的安培力作用。
4.1. 分子库仑力
根据库仑定律 [12] (见pp. 5-7)和图1所示的极化模型可知:两个分子之间的库仑力等效表现为它们的正电荷(原子核)与正电荷之间、正电荷与负电荷(核外电子)之间、负电荷与负电荷之间的相互作用力,具体包括
(2)
(3)
(4)
(5)
显然,(2)式和(3)式为库伦斥力、(4)式(5)式为库伦引力。其中,各式中的
均为真空电容率或真空介电常数。在MKSA单位制中,其值为
。
4.2. 分子安培力
根据安培定律 [12] (见pp. 103-109, 157)和分子简化模型知道:两个共轴且方向相同的分子载流回路(核外电子绕核运动的轨道回路)
和
(两个载流回路之间的距离近似为两个负电荷等效中心的距离)的分子电流
与
相互作用的安培力为
(6)
由于两个分子的核外电子绕核运动的方向总是倾向相同,因此这一分子电流的相互作用力为安培引力。其中,
为真空磁导率。在MKSA单位制中,真空磁导率
。
4.3. 分子力函数
综合(2)、(3)、(4)、(5)、(6)式,可将两个分子之间的等效作用力即分子力F的函数表达式表示为
(7)
这一函数表达式是比较繁杂的,但若相互作用的两个分子是完全相同的,那么它们之间的作用力表达式可以适当简化一些。如果令
、
、
、
,进一步将L近似为电子绕核运动的最大轨道圆周长,将I近似为相应的分子最大电流,那么,(7)式可简化为
(8)
再令
、
,将(8)再次简化为
(9)
很显然,(7)、(8)、(9)式中的第一项均表示分子斥力,第二项均表示分子引力。且各式中的极化距离
必须满足
,其中
为分子半径(下同)。
4.4. 分子力特值图线
不同物质的分子,(9)式对应的
、
以及各式中的
不相同。这里以氦分子为例予以说明。根据氦分子(原子)电量
,容易计算出其对应的
。另外,根据氦的分子半径 [13] (见p. 457)
,电子质量 [13] (见p. 452)
,结合经典电磁理论,也容易计算出其相应的载流回路长度
、分子电流
,进而计算出对应的
。因此,可将(9)、式改写为
(10)
通过对氦分子的计算说明:由于
(即
),因此,分子间的相互作用力主要是库仑力,而分子电流产生的安培力的影响是很微弱的。但是,安培力和库仑力同样具有深刻意义。
另外,结合氦分子实例数据,(1)式表示的极化距离约束函数可改写为
(11)

Figure 2. Molecular diagram of helium molecules with different n-values
图2. 氦分子不同n值分子力图线
为了对分子力进行更直观深入的研究,这里用mathematica软件结合(10)式和(11)式模拟了氦分子在不同n值的分子力图线,如图2所示是同一坐标系中氦分子
的分子力对比图线。
从图中可以看出:分子力平衡位置(即分子力
的位置)随n的取值增大而逐渐向左移;当n的取值过小和分子间距离r较大时,图线体现的总都是分子斥力;不同n值对应的图线下端恰好构成一条平滑曲线,而这一曲线恰好就是不考虑分子极化情况下的分子力图线,因分子无极化时分子力只有分子引力;随着分子间距离r的减小,不同n值分子力都逐渐趋于同一个定值。
结合图像深入研究表明,当n的取值为
时,图线反映的分子力变化规律与目前的认知情况( [14] : pp. 43-44; [15] )有很好的吻合度。同时可分析得出,分子间有效作用距离范围数量级 [14] (见p. 37, 45)为
。
5. 分子势能函数
分子力是保守力,即分子力满足
(12)
因此,分子之间必然存在分子势能。
5.1. 分子势能函数
令两个分子相距无限远时的分子势能为零,则根据(7)式,分子势能
可表示为
(13)
对于完全相同的两个分子,根据(9)式,可将(13)式简化为
(14)
其中,
、
和
的意义以及对应氦分子
、
的值如前所述。所以,氦分子的分子势能函数可表示为
(15)
特别说明:(13)式、(14)式、(15)式所表示的分子势能函数中的第一项均为分子斥力势能,第二项均为分子引力势能,其中的分子极化距离
均要受到(1)式或(11)式的约束。
5.2. 分子势能特值图线
如图3所示是用mathematica软件结合(15)式和(11)式拟合的氦分子的势能曲线。
从图中可以看出与图2类似的特点:分子力平衡位置即分子势能
最小的位置随n的取值增大而逐渐向左移;当n的取值过小和分子间距离r较大时,图线体现的总都是分子斥力势能;不同n值对应的图线下端,恰好构成一条平滑曲线,这一曲线实际就是不考虑分子极化情况下的分子势能图线,因分子无极化时分子势能只有分子引力势能;随着分子间距离r的减小,不同n值对应的分子势能都逐渐趋于同一个定值;分子间有效作用距离范围数量级为10−10 m;当n的取值为
时,图线能较好的反映氦分子势能变化规律。
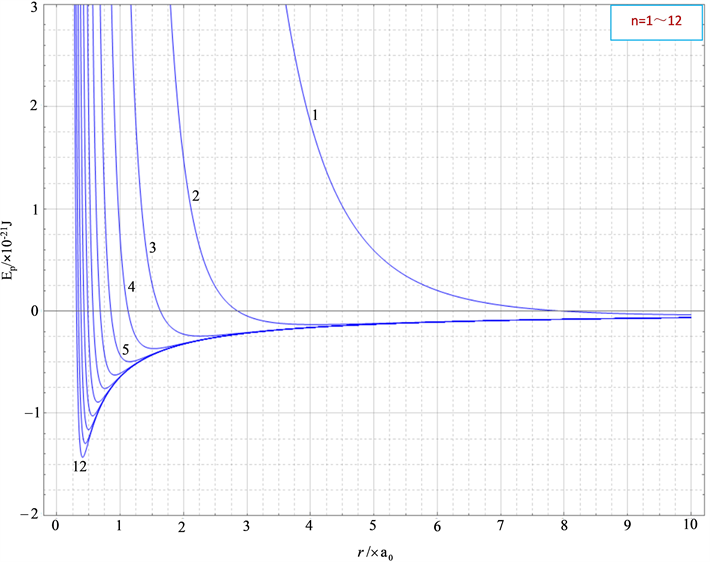
Figure 3. Molecular potential energy graph lines of helium molecules with different n-values
图3. 氦分子不同n值分子势能图线
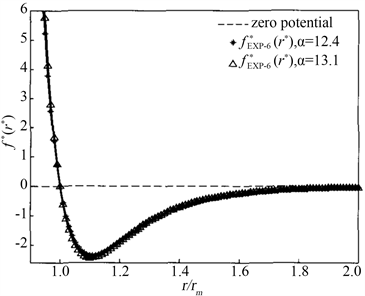
Figure 4. Semiempirical molecular force function graph line of helium molecule
图4. 氦分子半经验分子力函数图线

Figure 5. Bruch-McGee semiempirical potential energy function graph line for helium molecules
图5. 氦分子Bruch-McGee半经验势能函数图线
6. 比较分析
6.1. 文献呈现
如图4、图5所示是有关文献 [16] 对氦分子研究分别得出氦分子半经验分子力函数和氦分子半经验势能函数图线。
分别比较图2与图4、图3与图5,当n的取值在适当范围时,它们均能得出几乎相同的结果。这在一定程度上说明图1所示的分子极化模型的合理性。
6.2. 另一种分子极化模型
在对分子力和分子势能的研究中,我们还建立如图6所示的分子极化模型 [17] 。这种极化模型与图1所示的极化模型相反,即极化使得两分子的负电荷中心减小,称为分子电流吸引极化模型。

Figure 6. Molecular current attraction polarization
图6. 分子电流吸引型极化
根据前述氦分子的实例数据,得到这种极化模型对应的氦分子的分子力函数为
(16)
分子势能函数为
(17)
将(11)式表示的极化距离约束函数附加
条件后,用mathematica软件分别将把(16)式和(17)式与之结合,拟合氦分子在不同n值的分力函数图线和分子势能函数图线分别如图7和图8所示。
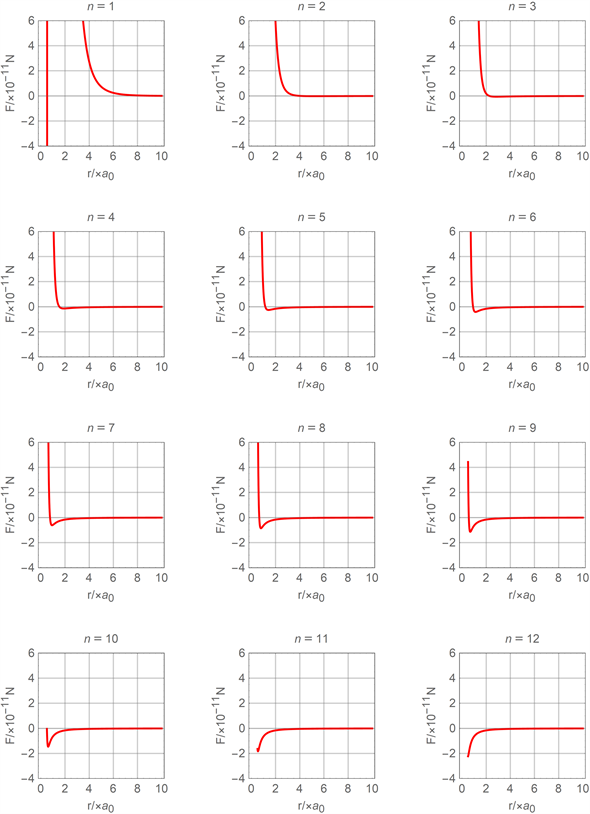
Figure 7. Comparison diagram of molecular force function of molecular current attractive polarization model
图7. 分子电流吸引极化模型分子力函数对比图线
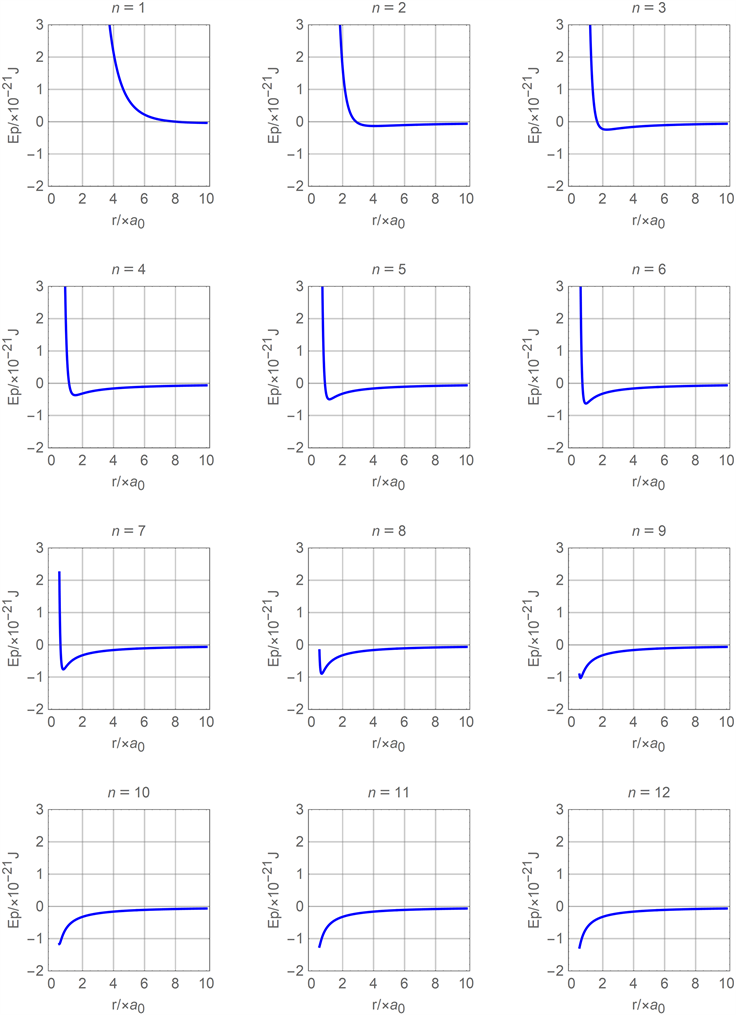
Figure 8. Comparison diagram of molecular potential energy function of molecular current attractive polarization model
图8. 分子电流吸引极化模型分子势能函数对比图线
从图7和图8中可以看出:当n取值过小时,不论分子间距离如何分子间都总是分子斥力或分子斥力势能;当n取值较大且分子间距离r较小时,分子斥力和分子斥力势能均随着分子间距离r的减小而急剧相对减小而消失。图7、图8体现的现象分别与图4、图5或图2、图3存在很大的差异性,且与目前关于分子力或分子势能的认知情况不能很好的相吻合,但在一定范围内(比如
)还是体现出与图2、图3的相似特性。说明图6所示的分子极化模型存在较大的局限性。
7. 结论
本文通过在基于设定的图1和图6所示的分子极化模型及(1)式表示的分子激化距离约束函数假设前提之下的对比研究,解释了分子力作用的本质,同时得到了一些很有价值的结果。
1) 分子力是分子中的电荷库仑力与分子电流的安培力共同作用的结果,但是库仑力的影响要明显得多。电荷库仑力与分子电流的安培力之间相差104数量级。
2) 在图2和图3所示的图线中,随着分子间距离r的减小,不同n值对应的分子力和分子势能都分别逐渐趋于同一个定值。这说明分子间距离不可能无限减小,存在一个最小值。
3) 相对图1所示的极化模型,图6所示的极化模型是非稳定极化模型。分子在按图6所示的极化模型极化过程中,当分子间距离减小到一定值时,极化模式将发生突变而按图1所示的极化模型极化,从而导致分子力和分子势能突变(即图7与图8中体现的分子斥力和分子斥力势能急剧相对减小而消失)。