1. 引言
原子干涉仪 [1] [2] [3] 具有非常高的精度,比光学干涉仪高十个数量级以上。因此,原子干涉仪可以应用于许多精确的测量领域,如测量重力加速度 [4] [5] [6] [7] 和重力梯度 [8] - [13] ,探测暗物质 [14] ,以及探测低频引力波 [15] 。自1991年 [1] 历史上第一台原子干涉仪诞生以来,原子干涉仪的发展非常迅速。但直到今天,原子干涉仪的优化工作仍在进行,特别是对一些实际工作环境的优化。目前,世界范围内对原子干涉仪的研究仍处于实验室原型阶段,在实验室以外的大型动态环境中对其进行进一步研究是非常重要的。
超冷原子云,由于原子动量的分布非常狭窄,矩形脉冲序列 [16] [17] 可用于实现具有较高保真度的原子干涉仪。但对于热冷原子云来说,原子动量的分布较宽,由于其场强恒定,矩形脉冲不能补偿由大原子速度引起的一些大的多普勒效应 [18] 。因此,在这种情况下,如果使用矩形脉冲,原子干涉仪不能达到其要求的保真度。与恒定振幅的矩形脉冲相比,一些具有不同场强的脉冲可能有能力补偿大的多普勒效应。形状脉冲 [19] [20] 是优化原子干涉测量法中的激光脉冲的技术之一,它被广泛地应用于核磁共振的研究。通过调制脉冲的振幅和相位来补偿多普勒效应,这种技术也可以用来改善原子干涉仪的性能。作为一种波形脉冲 [21] ,高斯脉冲通常被用来取代矩形脉冲,以改善热冷原子云中原子干涉仪的保真度 [22] [23] 。高斯脉冲对系统多普勒效应的补偿能力随着宽度和相位的变化而不同。通过使用具有适当宽度和振幅的优化高斯脉冲序列,可以有效减少系统多普勒效应。在本文中,我们通过用高斯脉冲序列取代矩形脉冲序列来优化原子干涉仪。用于研究原子干涉仪的原子是一个温度为100 μK的热冷原子集合。高斯脉冲序列对系统多普勒效应有抑制作用。不同宽度的高斯脉冲序列在原子干涉仪中产生不同的原子激发态概率。通过优化具有适当宽度的高斯脉冲序列,可以获得原子干涉仪激发态原子的最大期望概率。因此,优化后的高斯原子干涉仪可以应用于一些实际领域。
2. 原子干涉仪的基本原理
我们所考虑的原子干涉仪是一种March-Zehnder构型 [24] [25] 。激光与三能级原子的相互作用系统如图1所示。图中
和
为两个基态超精细结构,
为激发态。两个反方向传播的激光脉冲在
拉曼偏振排列中,频率为
,波矢为
将
和
耦合到
态上。两束激光L1和L2之间的频率差等于两个基态超精细能级的频率分裂。激光束L1将一个初始动量为
的原子从基态
到激发态
,相同时间内原子吸收动量从
增加到
,激光束L2激发原子从激发态
回到
,而原子获得一个光子的反冲动量,并且动量从
变为
。
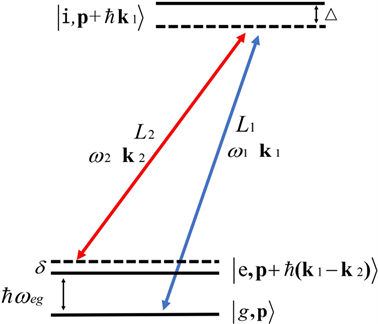
Figure 1. The Raman system of light field interactions with atoms. L1 and L2 are a pair of counter-propagating laser pulses, and their frequencies and wave vectors are
and
.
and
are two ground state hyperfine energy levels, and
is the upper energy level of the system. The energy level difference between the two hyperfine ground states is expressed as
. ∆ and
the single-photon detuning and the two-photon detuning, respectively
图1. 拉曼系统中的光场与原子的相互作用原子。L1和L2是一对反向传播的激光脉冲,它们的频率和波矢为
和
。
和
是两个基态的超精细能级,
是系统的上层能级。两个基态超精细结构的能级差为
。
和
分别是单光子失谐和双光子失谐
系统中的单光子失谐量
通常可达数GHz量级,此时自发辐射
可以忽略不计。因此,这个三级系统可以简化为一个有效的二级系统。其有效拉比频率为
,其中
是L1激光从
跃迁到
的拉比频率,
是L2激光从
跃迁到
的拉比频率。在一个有效的二能极系统中,
和
态分别为基态和激发态。
为双光子的失谐,可以写为:
, (1)
式中
是激光失谐,
是多普勒失谐,
是反冲频率。我们假设最初的态为:
,其演化时间为t,
和
的振幅变化为:
, (2)
, (3)
式中
,
,
,
为激光的有效相位;
是
和
的AC斯塔克效应。当
时,
。我们假设
,
,经过时间t的演化,我们分别找到原子在
和
的态为:
(4)
当
,原子等概率的分布在
和
上;但当
时,
和
态上的原子布局数正好相反。
如图2所示,原子干涉仪是靠着π/2 − π − π/2的脉冲序列来分裂、反转和重组原子 [26] 。原子最初的态为
其动量为
,t0时间内,原子与π/2脉冲相互作用,其中一半的原子获得两个光子的动量为
,同时它们的态变化我
,剩下的半数原子保持原来的
。因为这两部分原子的动量不同导致它们之间彼此分离,经过持续时间为T的自由演化,在t1时刻,π脉冲与两条路径上的原子相互作用,原子从
态变化到
,而
态上原子变为
。最后的结果是两个路径上的原子都发生了反转,紧接着,原子经历第二个持续时间的演化。在t2时刻,π/2脉冲与这些原子相互作用,又导致原子的态从
到
和
以及从
态到
和
态。对于原子干涉仪,如果有效的激光脉冲π/2 − π − π/2的脉冲序列为
及
。原子从
到
态的动量可以表达为
[27] 。
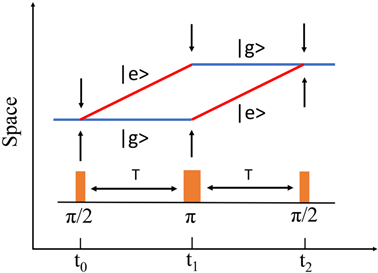
Figure 2. The principle diagram of Mach-Zehnder atom interferometer. Three single pulse pairs form a π/2 − π − π/2 pulse sequence consisting of two free evolutionary processes with time T. The pulse sequence causes atoms to split, reverse, and recombine
图2. Mach-Zehnder型原子干涉仪原理图。三个单一的脉冲对π/2 − π − π/2形成一个脉冲序列,两个自由演化过程组成时间为T。脉冲序列导致原子分裂、重新和重新结合
3. 优化高斯脉冲原子干涉仪的序列
传统的原子干涉仪中的脉冲序列由三个振幅恒定的矩阵型脉冲组成,对于具有速度分布的热冷原子,由于直角脉冲的场强恒定,矩形脉冲对多普勒效应的容忍度较低。我们可以用高斯脉冲序列代替矩形脉冲序列完成原子分裂、反转和再组合的过程。那么就必须要保证高斯脉冲在π/2分裂和π镜像脉冲的面积相等,三个脉冲高斯脉冲具有相等有效激光相位和有效作用面积接近π/2和π。此外除了脉冲形状不同之外,要保证高斯脉冲序列的所有交互时间与矩形脉冲的交互时间保持一致。由于高斯脉冲的振幅随时间变化,在模拟原子与高斯脉冲的相互作用时,高斯脉冲可以被划分为n个相同长度的时域切片,每一个切片都可以被视为一个矩形脉冲,当原子与第N个时间片相互作用后的状态可描述为:
, (5)
式中C和S分别定义为 [28] :
, (6)
, (7)
其中
是脉冲持续。一个高斯脉冲等于该脉冲被分成的n个后全部时间。初态为
和
的原子与高斯脉冲相互作用t时间后,
(8)
因此,原子干涉仪中原子使用高斯脉冲后末态可表示为:
(9)
高斯脉冲的振幅大小用
,其中
是高斯脉冲振幅的极大值,
是高斯脉冲的宽度,当
时,振幅A达到它的极大值
。在这两种类型的脉冲序列中,三个激光的有效相位分别为为
及
。高斯脉冲序列和矩形脉冲序列中每个对应的单个脉冲的作用时间相同。保证作用的区域是π/2或π,当温度为100 μK时,我们模拟原子的初始动量分布为:
, (10)
其中p是原子动量,范围从
到
,
,
,
。模拟参数原子的失谐为
,激光脉冲强度
,激光的失谐为
,且有效拉比频率为
。基于上述条件,我们比较了在激发态
下不同宽度矩形脉冲和高斯脉冲在π/2和π脉冲下的概率。当原子被单一的π/2脉冲作用时,原子在
态下的概率分别为
,如图3所示。
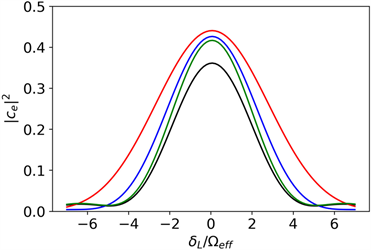
Figure 3. The probability of the atom in the excited state vs laser detuning when the rectangular pulse and three Gaussian π/2 pulses with different widths are used. The black, green, blue and red curves are the results for the π/2 pulses p0, p1, p2, and p3, respectively
图3. 当矩形脉冲和三种不同宽度的π/2高斯脉冲作用后,原子处于激发态与失谐的关系曲线。黑色、绿色、蓝色和红色曲线是π/2脉冲的结果
很显然不同的高斯脉冲宽度对应不同的概率,优化后的高斯脉冲对应最大的概率及宽度(图3红色曲线)。当原子与π脉冲作用时,原子在
态下的概率分别为
,如下图4。
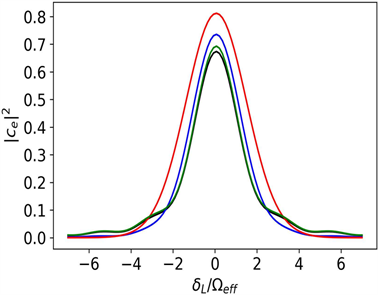
Figure 4. The probability of the atom in the excited state vs laser detuning when the rectangular pulse and three Gaussian π pulses with different widths are used. The black, green, blue and red curves are the results for the π pulses
, respectively
图4. 当矩形脉冲和三种不同宽度的π高斯脉冲作用后,原子处于激发态的概率与失谐的关系曲线。黑色、绿色、蓝色和红色曲线是π脉冲的结果
与π/2脉冲时相互作用的情况类似,也有不同的概率和宽度。最理想的概率和宽度对应于优化的π高斯脉冲,如图4的红色曲线所示。二者的优化细节将在下面详细说明。
从图3和图4中我们可以看到,对于高斯脉冲,无论是π/2脉冲或π脉冲,相比于矩形脉冲在
态都具有较高的概率峰值。

Table 1. The effective Rabi frequencies of the rectangular and Gaussian pulses as the single π/2 and π pulses
表1. 矩形脉冲和高斯脉冲在π/2和π的有效拉比频率
对于原子干涉仪,我们需要考虑到整个π/2 − π − π/2激光脉冲序列。我们假设在激光脉冲序列中的三个单一激光脉冲的有效相位为0、π/4和0,且在高斯脉冲中π脉冲的宽度是π/2脉冲宽度的两倍。通过结合表1中可以得到三个脉冲序列。分别为
、
、
。然后我们计算了原子在
态经历这三个脉冲序列后的概率。如图5所示,黑色曲线表示当矩形脉冲序列
作用在原子干涉仪上,原子处于
态时的概率与激光失谐的关系;绿色和蓝色的曲线表示高斯脉冲序列
和
作用时,原子处于
态的概率与激光失谐的关系。
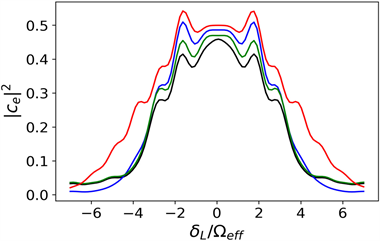
Figure 5. The probability of the atom in the state
as a function of laser detuning
after experiencing rectangular and Gaussian pulse sequences. The black curve indicates the result of using a rectangular pulse sequence. The red curve, green curve and blue curve indicate the results of using three Gaussian pulse sequences with different widths, respectively
图5. 经过矩形和高斯脉冲序列后,原子处于
态的概率是激光失谐
的函数。黑色曲线表示使用矩形脉冲序列的结果。红色、绿色和蓝色曲线表示的是使用三个不同宽度的不同宽度的高斯脉冲序列
从图5中,我们可以看到在绿色和蓝色曲线更接近中心位置,并且对系统的失谐有一个很好的容忍。
为了找到优化的高斯脉冲序列,我们需要改变高斯脉冲的宽度,使概率更接近理想值。为了做到这一点,我们在高斯脉冲的宽度中加入一个比例因子,并计算比例因子的变化所带来的概率。理想状态下,激光失谐为0时,经过一个脉冲序列后,处于
态上的原子概率为0.5。图六是对求解了高斯脉冲宽度的比例因子在0.2到1.6范围内变化时,对应的处于
态的原子概率。处于
态的原子概率为0.5时,比例因子最佳。结果展示脉冲的宽度与脉冲p2的宽度成正比,比例因子
的范围是0.2到1.6。如图6所示,当
时,我们得到一个新的高斯脉冲序列
。当我们在原子干涉仪中使用这个高斯脉冲序列时,处于
态的原子概率的中心值等于理想值0.5,结果如图5中的红色曲线所示。
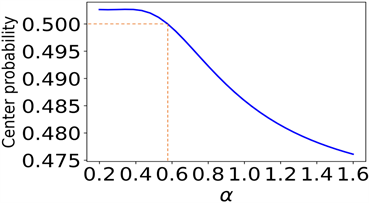
Figure 6. The variation of the central probability of the atoms in the state
with the scaling factor
图6. 在
态上原子中心概率的变化随着比例因子
的变化而变化
尽管所有的高斯脉冲序列都表现出降低失谐效应的效果,但只有由具有适当宽度的高斯脉冲组成的脉冲序列才能在整个干涉仪过程中使两种状态下的原子概率更接近理想值。选择优化的高斯脉冲序列不仅使最终的概率更接近期望值,而且还提高了原子干涉仪对系统多普勒效应的容忍度。
4. 结论
在本论文中,为了提高热冷原子干涉仪的精度和耐受性,我们提出了一种用典型的高斯脉冲序列代替矩形脉冲序列来优化原子干涉仪的方法。数值结果显示,当原子干涉仪为典型的高斯脉冲序列驱动时,原子干涉仪的激发态原子的概率增加。同时,当原子被高斯脉冲序列驱动时,带宽也变得更宽。
事实证明,高斯脉冲序列可以有效地减轻多普勒效应的影响,可以利用高斯脉冲替代矩形脉冲。此外,不同宽度的高斯脉冲序列将导致原子处于激发态的概率也不同。本文通过改变高斯脉冲的宽度,我们建立最佳的高斯脉冲序列,从而使原子干涉仪达到最理想的概率和带宽。得到了优化后的高斯脉冲序列驱动的原子干涉仪具有最高的精度和对多普勒效应的容忍度。因此,优化后的高斯脉冲序列驱动的原子干涉仪将有更多的实际应用。