抗乳腺癌候选药物的优化建模

Optimal Modeling of Candidate Drugs for Anti Breast Cancer

摘要: 乳腺癌是一种致死率较高的癌症。人体的乳腺上皮细胞在多种致癌因子的共同作用下发生增殖失控而形成癌变。本文针对提供的ERα拮抗剂信息，通过建立化合物生物活性的定量预测模型和ADMET性质的分类预测模型，为同时优化ERα拮抗剂的生物活性和ADMET性质提供预测服务。首先利用随机森林算法评价变量重要度大小筛选出贡献度排名前60的分子描述符；然后通过高相关性变量去耦合，对前60个分子描述符进行高相关性滤波处理，从而得到前20个对生物活性最具有显著影响的分子描述符；最后基于高相关度变量滤波算法保证了降维后分子描述符之间的独立性，对分子描述符之间的相关程度进行可视化，从而验证了其合理性。其次，在通过尝试构建多元线性回归方程解决此题时，发现时序残差图的异常点较多后，我们构建了多元非线性回归模型。首先利用python对变量进行标准化操作，得到标准化指标；其次利用问题一得到的前20个分子描述符作为自变量，通过对一些数值较大的变量取自然对数，建立了用于预测生物活性的多元非线性回归模型。最后找出影响ADMET性质的前10个分子描述符，并分别对各分子描述符之间的相关程度进行可视化；其次利用全连接单层神经网络优秀的非线性映射能力构建5个化合物的分类预测模型，并通过各个化合物的分类预测模型的交叉熵损失图说明了模型有着较高的准确度。

Abstract: Breast cancer is a kind of cancer with high mortality. Under the combined action of various car-cinogenic factors, human breast epithelial cells undergo uncontrolled proliferation and form can-cerous transformation. This article aims to provide prediction services for optimizing the biological activity and ADMET properties of ERα antagonists by establishing a quantitative prediction model for compound biological activity and a classification prediction model for ADMET properties. Firstly, the random forest algorithm is used to evaluate the importance of variables to screen out the top 60 molecular descriptors of contribution degree; then, by decoupling highly correlated variables, the first 60 molecular descriptors were subjected to high correlation filtering to obtain the top 20 mo-lecular descriptors that had the most significant impact on biological activity; finally, based on the high correlation variable filtering algorithm, the independence between molecular descriptors after dimensionality reduction was ensured, and the degree of correlation between molecular de-scriptors was visualized to verify its rationality. Secondly, when attempting to construct a multiple linear regression equation to solve this problem, we found that there were many outliers in the time series residual plot, and then constructed a multiple nonlinear regression model; firstly, use Python to standardize variables and obtain standardized indicators; secondly, the first 20 molecu-lar descriptors obtained in question 1 are used as independent variables, and a multivariate non-linear regression model for predicting biological activity is established by taking natural logarithm for some variables with large values. Finally, identify the top 10 molecular descriptors that affect the properties of ADMET and visualize the degree of correlation between each molecular descriptor; secondly, the classification prediction model of five compounds was constructed by using the excel-lent nonlinear mapping ability of the fully connected single-layer neural network, and the cross en-tropy loss diagram of the classification prediction model of each compound showed that the model had high accuracy.

1. 引言

近年来乳腺癌已成为致死率较高的癌症之一，乳腺癌是乳腺上皮细胞在多种致癌因子的作用下，发生增殖失控的现象。乳腺癌的发展与雌激素受体密切相关，有研究发现，雌激素受体α亚型在不超过10%的正常乳腺上皮细胞中表达，但大约在50%~80%的乳腺肿瘤细胞中表达；而对ERα基因缺失小鼠的实验结果表明，ERα确实在乳腺发育过程中扮演了十分重要的角色。因此，ERα被认为是治疗乳腺癌的重要靶标，能够拮抗ERα活性的化合物可能是治疗乳腺癌的候选药物。目前，在药物研发中，为了节约时间和成本，通常采用建立化合物活性预测模型的方法来筛选潜在活性化合物。根据提供的ERα拮抗剂信息(1974个化合物样本，每个样本都有729个分子描述符变量，1个生物活性数据，5个ADMET性质数据)，构建化合物生物活性的定量预测模型和ADMET性质的分类预测模型，从而为同时优化ERα拮抗剂的生物活性和ADMET性质提供预测服务。建立数学模型研究下列问题：

1、针对1974个化合物的729个分子描述符进行变量选择，分析变量对生物活性影响的重要性进行排序，给出前20个对生物活性最具有显著影响的分子描述符(即变量)，然后说明分子描述符筛选过程及其合理性。

2、结合问题一，选用不超过20个分子描述符变量，构建化合物对ERα生物活性的定量预测模型，对50个化合物进行IC₅₀值和对应的pIC₅₀值预测，并将结果分别填入对应的表。

3、利用ADMET数据，分别构建化合物的Caco-2、CYP3A4、hERG、HOB、MN的分类预测模型。通过5个分类预测模型，对50个化合物进行相应的预测，并将结果填入对应的表。

4、寻找并阐述化合物的分子描述符，以及这些分子描述符在什么取值或者处于什么取值范围时，能够使化合物对抑制ERα具有更好的生物活性，同时具有更好的ADMET性质，在给定的五个性质中，至少选择三个性质较好。

2. 问题分析

研究发现，乳腺癌的发展与雌激素受体密切相关，而对ERα基因缺失小鼠的实验结果表明，ERα在乳腺发育过程中扮演了十分重要的角色；因此能够拮抗ERα活性的化合物可能是治疗乳腺癌的候选药物。所以通过预测化合物的生物活性来筛选药物是高效且快速的方法，为了解决这个问题，我们进行了具体分析。

2.1. 问题一的分析

问题一要求我们建立模型针对分子描述符进行变量筛选，将变量对生物活性影响的重要性进行排序，并按照降序排列筛选出前20个对生物活性最具有影响力的分子描述符。

2.2. 问题二的分析

问题二要求我们选择不超过20个分子描述符变量，构建化合物对ERα生物活性的定量预测模型，然后使用构建的预测模型，对文件“ERα_activity.xlsx”的test表中的50个化合物进行IC₅₀值和对应的pIC₅₀值进行预测。首先我们可以选用第一题所得到的前20个对生物活性最具有显著影响的分子描述符表示为自变量，生物活性表示为因变量；其次构建多元非线性回归方程解出各因变量的系数，最后得到预测模型。

2.3. 问题三的分析

问题三要求分别构建化合物的Caco-2、CYP3A4、hERG、HOB、MN的分类预测模型，分类是指定性输出预测，传统的多元回归分析预测值不能落入0-1区间，因此不能针对解决二分变量(0,1编码)的预测问题，因此，本题将应用全连接的单层神经网络分别构建化合物的Caco-2、CYP3A4、hERG、HOB、MN的分类预测模型。首先我们利用题一的模型找出分别影响Caco-2、CYP3A4、hERG、HOB、MN的10个特征，然后通过找出来的10个特征分别使用全连接的单层神经网络构建分类预测模型。

2.4. 问题四的分析

问题四要求寻找化合物的某些分子描述符并得到其取值范围，使得化合物对抑制ERα具有更好的生物活性，同时具有更好的ADMET性质，基于问题一和问题三筛选出的分子描述符，我们采用博弈论的方法将问题四看成是卖方与买方的对策问题，进而用博弈论中的零和二人混合对策来进行数学描述，在极大化化合物对抑制ERα具有更好的生物活性的情况下，同时具有更好的ADMET性质。

3. 模型假设

1、所有化合物的生物活性值、分子描述符、ADMET性质的数据测量正确；

2、没有其他的分子描述符会对化合物的生物活性值和ADMET性质有影响；

3、建立模型时假设不考虑人为因素对数据的影响；

4、在优化主要变量时认为所提出的预测模型结果准确。

4. 符号说明

由于文章符号较多，为了方便阅读，将所有符号整理如下

5. 问题一的模型建立与求解

5.1. 模型的建立

问题1模型建立过程如图1。

Figure 1. Problem 1 flowchart

图1. 问题一流程图

5.2. 模型的求解

5.2.1. 数据预处理

数据预处理是从数据中检测，纠正或者损坏不准确，不适用模型的记录的过程，为了提高要进行观察和分析的数据的质量，我们在进行建模前去掉全为0的分子描述符的列 [1] 。

利用Python实现随机森林算法，综合考虑到算法速度和算法准确率，设定K = 500，M = 100。运行程序得到504个分子描述符的贡献度排名，将贡献度由大到小排序。考虑到下一步的高相关性滤波操作会对进一步变量进行降维，故在这一步中先筛选出排名处于前60的分子描述符，如下表1所示。可以发现排名为60的分子描述符对pIC₅₀值的归一化贡献度只有0.284%，且前60个分子描述符贡献度有83.78%,说明选取贡献度排名前60名的分子描述符已经可以有足够的信息来预测pIC₅₀值。

Table 1. Name and contribution size of the top 60 molecular descriptors with contribution ranking

表1. 贡献度排名前60的分子描述符名称及贡献度大小

5.2.2. 高相关性变量去耦合

本题中各变量间为非线性关系，选择距离相关系数作为衡量变量间相关性的指标 [1] 。对于两个随机向量， $x\in R^p$ ， $y\in R_q$ ，记 $\left(x,y\right)=\left\{\left(x_i,y_i\right):i=1,\cdots ,n\right\}$ 为观察到的随机样本，x，y间的距离相关系数(dCor)可以定义为：

$R^2\left(x\mathrm{,}y\right)=\frac{v^2\left(x\mathrm{,}y\right)}{\sqrt{v^2\left(x\mathrm{,}x\right)v^2\left(y\mathrm{,}y\right)}}$ (5.1)

其中：

$v^2\left(x,y\right)=\frac{1}{n^2}{\displaystyle \underset{i,j=1}{\overset{n}{\sum }}}{A}_{i,j}{B}_{i,j}$ (5.2)

$v^2\left(x,y\right)=\frac{1}{n^2}{\displaystyle \underset{i,j=1}{\overset{n}{\sum }}}{A}_{i,j}{B}_{i,j}$ (5.3)

$A_{i,j}={\Vert x_i-x_j\Vert }_2-\frac{1}{n}{\displaystyle \underset{k=1}{\overset{n}{\sum }}}{\Vert x_k-x_j\Vert }_2-\frac{1}{n}{\displaystyle \underset{l=1}{\overset{n}{\sum }}}{\Vert x_i-x_l\Vert }_2+\frac{1}{n^2}{\displaystyle \underset{k,l=1}{\overset{n}{\sum }}}{\Vert x_k-x_l\Vert }_2$ (5.4)

$B_{i,j}={\Vert y_i-y_j\Vert }_2-\frac{1}{n}{\displaystyle \underset{k=1}{\overset{n}{\sum }}}{\Vert y_k-y_j\Vert }_2-\frac{1}{n}{\displaystyle \underset{l=1}{\overset{n}{\sum }}}{\Vert y_i-y_l\Vert }_2+\frac{1}{n^2}{\displaystyle \underset{k,l=1}{\overset{n}{\sum }}}{\Vert y_k-y_l\Vert }_2$ (5.5)

同理可计算：

$v^2\left(x,x\right)=\frac{1}{n}{\displaystyle \underset{i,j=1}{\overset{n}{\sum }}}{A}_{i,j}^2$ (5.6)

$v^2\left(y,y\right)=\frac{1}{n}{\displaystyle \underset{i,j=1}{\overset{n}{\sum }}}{B}_{i,j}^2$ (5.7)

根据题目要求，去耦合后的分子描述符之间应该具有中相关以下的相关性，故将距离相关系数(dCor)的阈值设为0.6。基于此，对表1中的分子描述符进行相关性检验。首先计算两两分子描述符间的距离相关系数，然后判断两者的相关系数是否大于所设阈值。若大于，则说明两分子描述符相关性高，对两分子描述符的贡献值排名靠后的那一分子描述符采取删除操作。若小于，则说明两分子描述符间并不强相关，则将两分子描述符都暂时予以保留。之后重复上述操作，直至遍历结束。使用python编写去耦合程序，程序流程图如图2所示。

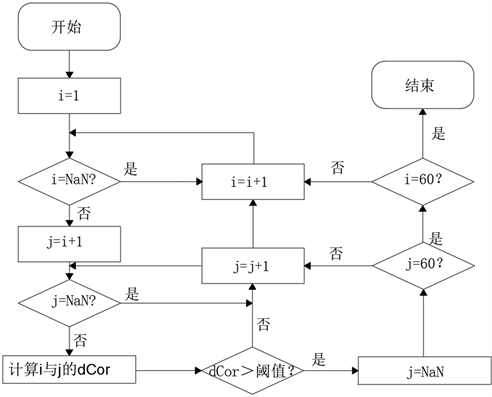
Figure 2. Decoupling program flowchart

图2. 去耦合程序流程图

根据此去耦合程序，对表1中分子描述符进行高相关性滤波处理，前60个贡献值高的分子描述符经滤波处理后剩余20个分子描述符，如下表2所示。降维后的这20个分子描述符是对生物活性最具有显著影响的分子描述符，供下文建立模型时使用 [2] 。

Table 2. Residual molecular descriptors after filtering processing

表2. 滤波处理后剩余分子描述符

5.3. 合理性评价

从分子描述符降维过程中采用的算法及处理流程来看：随机森林得到的分子描述符贡献度排名，保留排名靠前的分子描述符从而保证了所选取变量与因变量之间的相关性，而设计的基于距离相关性高相关度变量滤波算法则保证了降维后分子描述符之间的独立性，可根据所提取的分子描述符之间的距离相关系数计算结果，对分子描述符之间的相关程度进行可视化，如图3所示。可见选取的前20个分子描述符之间相关性低，独立性较好。

Figure 3. Correlation distribution map of the top 20 main molecular descriptors

图3. 前20个主要分子描述符的相关性分布图

6. 问题二的模型建立与求解

6.1. 数学模型的建立

Figure 4. Question 2 flowchart

图4. 问题二流程图

问题二的流程图如图4所示，生物活性通常受到多个因素的影响，根据问题1我们选择前20个对生物活性最具有显著影响的分子描述符作为变量，建立用于预测生物活性的多元线性回归模型，见式

$y={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k+\epsilon$ (6.1)

式中y为生物活性值；x为20个生物活性影响分子描述符； $\beta$ 为待求系数； $\epsilon$ 为随机误差，

$\epsilon ~N\left(\mathrm{0,}{\sigma }^2\right)$ (6.2)

将式(6.1)写成误差方程的形式，如下

$V={\beta }_0+{\beta }_1{x}_1+{\beta }_2{x}_2+\cdots +{\beta }_k{x}_k+\epsilon -y$ (6.3)

式中， $V$ 为改正数，由于pIC₅₀由多变量控制，因此，可将式(6.2)写为矩阵形式，见式(6.4)：

$V=A\beta -Y$ (6.4)

式中， $V={\left[\begin{array}{llll}{v}_1\hfill & v_2\hfill & \cdots \hfill & v_n\hfill \end{array}\right]}^{\text{T}}$ ， $\beta ={\left[\begin{array}{llll}{\beta }_0\hfill & {\beta }_1\hfill & \cdots \hfill & {\beta }_n\hfill \end{array}\right]}^{\text{T}}$ ， $Y={\left[\begin{array}{llll}{y}_1\hfill & y_2\hfill & \cdots \hfill & y_n\hfill \end{array}\right]}^{\text{T}}$ ，

$A=\left[\begin{array}{ccccc}1& x_{11}& x_{21}& \cdots & x_{k1}\\ 1& x_{21}& x_2& \cdots & x_{k2}\\ ⋮& ⋮& ⋮& & ⋮\\ 1& x_{1n}& x_{2n}& \cdots & x_{kn}\end{array}\right]$

由最小二乘准则可得，待定系数解算公式为， $\beta ={\left(A^{\text{T}}A\right)}^{-1}{A}^{\text{T}}Y$ ，将 $\beta$ 带入式(6.1)即可求得预测pIC₅₀值。

由于影响因子之间单位不一致，容易出现量纲不同的情况，因此，本文在解算时，使用参数中心化，以去除量纲的影响。

将上述的待定系数解算公式进行参数中心化变更，见式(6.5)：

$\bar{\beta }={\left(A_s^{\text{T}}{A}_s\right)}^{-1}{A}_s^{\text{T}}{y}_s$ (6.5)

式中， $A_s=\left[\begin{array}{cccc}{x}_{11}-{\bar{x}}_1& x_{21}-{\bar{x}}_2& \cdots & x_{k1}-{\bar{x}}_k\\ x_{12}-{\bar{x}}_1& x_{22}-{\bar{x}}_2& \cdots & x_{k2}-{\bar{x}}_k\\ ⋮& ⋮& & ⋮\\ x_{1n}-{\bar{x}}_1& x_{2n}-{\bar{x}}_2& \cdots & x_{kn}-{\bar{x}}_k\end{array}\right]$ ， $y_s=\left[\begin{array}{c}{y}_1-\bar{y}\\ y_2-\bar{y}\\ ⋮\\ y_n-\bar{y}\end{array}\right]$

但在使用MATLAB软件求解过程中，我们发现经过7次对异常点进行处理后的时序残差图仍存在较多的异常点，如下图5所示，所以下面我们考虑构建多元非线性回归模型。

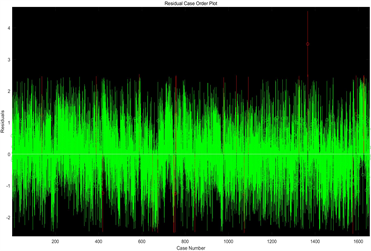
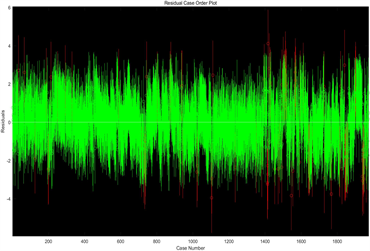(a)(b)

Figure 5. Time series residual comparison chart, (a) Residual diagram of the first running time sequence; (b) Residual diagram of the seventh running time sequence

图5. 时序残差对比图，(a) 第一次运行时序残差图；(b) 第七次运行时序残差图

与多元线性回归相对应的是多元非线性回归，然而多元非线性回归能够对因变量的影响产生更加重要的意义。如本题中预测pIC₅₀中，共有20个变量对因变量产生影响，应用多元线性回归的实用意义很大，在实际应用中变量之间的非线性变化，以及交互项对因变量的的预测产生重要的影响，非线性变化的加入也能够让因变量得到更加准确的效果。多元非线性回归的公式如下所示：

$Zy=f\left(Z_1\right)+f\left(Z_2\right)+f\left(Z_3\right)+\cdots +f\left(Z_k\right)$ (6.6)

这里的指非线性函数，包括幂次、指数、曲线、对数函数等。这里还应该注意的是，由于不同的指标具有不同的单位，不同的单位加入到公式运算中，虽然得到了如上公式中的系数，但这时的系数值大小不能代表该指标的重要性权重。所以本例中应用了Python软件进行标准化的操作，得到了标准化指标。

基于第二问主要变量的确定，记pIC₅₀为y。以下将构建pIC₅₀与20个主要变量的回归模型。自变量符号如下表3所示：

Table 3. Variable symbol table

表3. 变量符号表

首先我们选用第一题所得到的前20个对生物活性最具有显著影响的分子描述符作为20个变量，其次我们使用python构建多元非线性回归得到预测模型。最后我们将结果分别填入相应的test表中。

6.2. 数学模型的求解

我们用python软件的相关性分析功能，对各自变量之间进行相关性检验，发现变量之间没有很高的相关性，所以我们对一些数值较大的变量进行取自然对数处理，以此来降低其数值大小。最后我们将train表中的数据作为模型训练样本，test表中的数据作为预测样本并与实际值进行比较。

根据python软件运行结果，得到新的多元非线性回归方程模型：

$\begin{array}{c}y=6.7839+0.2573x_1-0.017\ln x_2-0.0467x_3+1.3994x_4+0.4915x_5\\ -0.086x_6+2.5641x_7-0.0043x_8+0.158x_9-0.3705x_{10}\\ +0.1249x_{11}-0.5103x_{12}-1.4556x_{13}-0.0174x_{14}+0.289\ln x_{15}\\ +0.1070x_{16}+0.0325x_{17}+0.0132\ln x_{18}-0.0112x_{19}-14.1272x_{20}\end{array}$ (6.7)

多元非线性回归预测值与实际值对比图如下图6所示，我们可以得到pIC₅₀预测值与实际值之间的差值在0.2以内，有着较高的准确度，因此可以用来进行pIC₅₀值的预测。

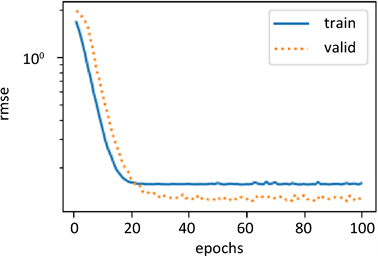
Figure 6. Comparison between predicted and actual values of multiple nonlinear regression

图6. 多元非线性回归预测值与实际值对比图

7. 问题三的模型建立与求解

7.1. 数学模型的建立

Figure 7. Problem 3 Flowchart

图7. 问题三流程图

问题三的求解过程如图7，通过利用题一的模型我们可以分别得到前10个对化合物的Caco-2、CYP3A4、hERG、HOB、MN最具有显著影响的分子描述符，如下表4所示，供下文分别建立Caco-2、CYP3A4、hERG、HOB、MN损失预测模型时使用。

Table 4. Five ADMET Properties

表4. 五种ADMET性质

通过对分子描述符之间的相关程度进行可视化，如图8所示。可见分别选取的前10个分子描述符之间相关性低，独立性较好。

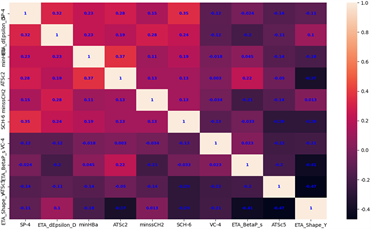
(a) [Caco-2](b) [CYP3A4]

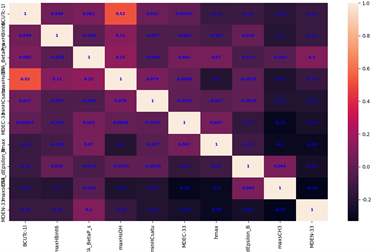
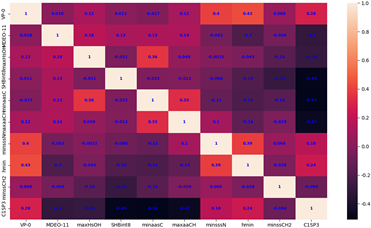(c) [hERG] (d) [HOB](e) [MN]

Figure 8. Correlation distribution map of the top 10 main molecular descriptors

图8. 前10个主要分子描述符的相关性分布图

从数据类型上来看，分子描述符之间可能具有高度非线性关系。全连接单层神经网络是人工智能网络的一个典型算法，其本身具有很强的非线性映射能力，非常适合解决一些非线性问题 [3] 。另外其网络拓扑结构简单，而且具有较高的计算精度。因此在此问中，我们将样本数据集数据进行标准化处理之后，采用train数据用于全连接单层神经网络模型训练，使用test数据对模型精度进行验证以评价模型合理性，本题我们选择只有一层的全连接神经网络，即二分类logistic回归模型。

对于维度为m + 1特征为x样本的二分类问题，有负类记为0，正类记为1，即对于类别y，有 $y\in \left(\mathrm{0,1}\right)$ 我们期望找到一个 $h_{\theta }\left(x\right)$ ，使得

$0\le h_{\theta }\left(x\right)\le 1$ (7.1)

其中，θ为待优化的参数，使得在对未知类别的样本x₀分类时， $h_{\theta }\left(x_0\right)$ 为样本为正类的概率。即分类准则如下：

$y_0=(\begin{array}{ll}0,\hfill & \text{if}{h}_{\theta }\left(x_0\right)<0.5\hfill \\ 1,\hfill & \text{if}{h}_{\theta }\left(x_0\right)\ge 0.5\hfill \end{array}$ (7.2)

在线性回归中，我们常找一组参数

$\theta =\left(\begin{array}{c}{\theta }_0\\ {\theta }_1\\ ⋮\\ {\theta }_m\end{array}\right)$

计算

$f\left(x\right)={\theta }^{\text{T}}x$ (7.3)

设置阈值T，通过 $f\left(x\right)$ 与T的大小关系判断正负类。

而在Logistic回归中，我们引入Sigmoid函数

$g\left(z\right)=\frac{1}{1+{\text{e}}^{-z}}$ (7.4)

Logistic回归取hypothesis function为

$\begin{array}{c}{h}_{\theta }\left(x\right)=g\left({\theta }^{\text{T}}x\right)=\frac{1}{1+{\text{e}}^{{\theta }^{\text{T}}x}}\\ =p\left(y=1|x;\theta \right)=p\left(y=0|x;\theta \right)\end{array}$ (7.5)

即 $h_{\theta }\left(x\right)$ 等价于正类的概率，由Sigmoid函数图像可知，当 ${\theta }^{\text{T}}x\ge 0$ 时，判定为正类，当 ${\theta }^{\text{T}}x<0$ 时，判定为负类。

与线性回归问题类似，Logistic同样需要定义代价函数使用梯度下降法优化参数

由于Sigmoid函数的使用，若使用与线性回归相同的二次损失函数，优化问题将变为非凸问题，即可能存在很多局部最优解。Logistic回归采用以下损失函数：

$\text{cost}\left(h_{\theta }\left(x\right),y\right)=(\begin{array}{ll}-\log \left(h_{\theta }\left(x\right)\right)\mathrm{,}\hfill & \text{if}y=1\hfill \\ -\log \left(1-h_{\theta }\left(x\right)\right)\mathrm{,}\hfill & \text{if}y=0\hfill \end{array}$ (7.6)

对于样本数目为n的训练集，定义目标函数为：

$\begin{array}{c}J\left(\theta \right)=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}}\text{cost}\left(h_{\theta }\left(x^{\left(i\right)}\right),y^{\left(i\right)}\right)\\ =-\frac{1}{n}[{\displaystyle \underset{i=1}{\overset{n}{\sum }}}{y}^{\left(i\right)}\log (h_{\theta }\left(x^{\left(i\right)}\right)+\left(1-y^{\left(i\right)}\right)\log \left(1-h_{\theta }\left(x^{\left(i\right)}\right)\right]\end{array}$ (7.7)

优化目标为：找到令 $J\left(\theta \right)$ 最小的θ。

7.2. 模型求解和分析

各个化合物的分类预测模型的交叉熵损失图如下图9所示，从图中可以观察到预测值与实际值的趋势大体一致，误差较小，所以模型较为合理，可以用来预测ADMET性质的值。

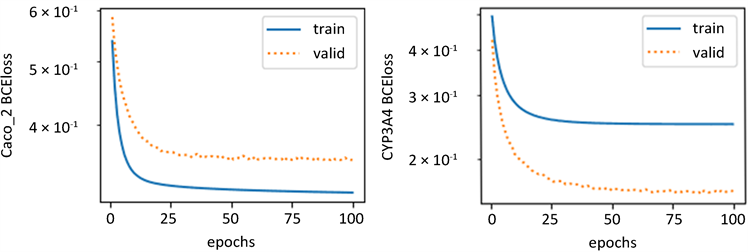
(a) [Caco-2] (b) [CYP3A4]

(c) [hERG](d) [HOB]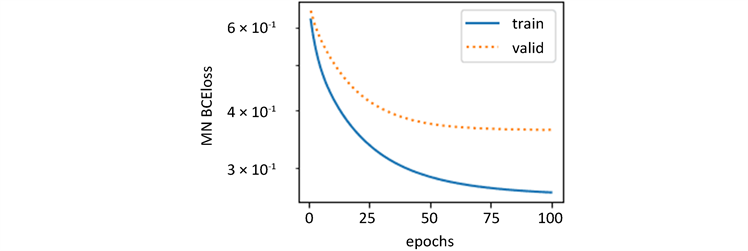(e) [MN]

Figure 9. Cross entropy loss graph of top 10 molecular descriptors of five ADMET properties

图9. 五种ADMET性质的前10个分子描述符的交叉熵损失图

8. 模型评价

8.1. 模型的优点

1) 充分考虑了各分子描述符与生物活性值之间的非线性关系，使用了随机森林回归、距离相关系数等适用于处理非线性特征的方法。所获得的主要变量意义明确，符合实际。

2) 针对主要变量与ADMET性质之间复杂的关系，选用了全连接的单层神经网络机器学习算法，同时数据集与测试集分开，所得到的结果最大相对误差很小，所建立的预测模型精度、鲁棒性表现优秀。

3) 使用博弈论模型，符合分子描述符实际筛选情况，能更好的找到既具有较高生物活性和较好ADMET性质的分子描述符。

4) 算法速度快，响应性好。

8.2. 模型的缺点

1) 模型过于理想化，应该考虑细分因素深度探究，升华模型。

2) 本文构建的神经网络预测模型训练样本数较少，日后可获得更多数据对其进行修正。

3) 多元非线性回归模型有更好的函数形式，由于变量过多，我们没有进行多次尝试得到更优的一个函数。