基于监控视频背景建模的一类非凸矩阵优化算法研究

Research on a Class of Nonconvex Matrix Optimization Algorithm Based on Surveillance Video Background Modeling

摘要: 为了实现稳健的低秩–稀疏矩阵分解，本文考虑非凸非光滑优化模型，其中矩阵的秩函数采用奇异值的Capped-l₁松弛，矩阵的l₀范数采用矩阵的l₁范数松弛。首先，给出了适用于矩阵问题的Capped-l₁阈值算子。其次，提出了交替方向乘子法求解我们的非凸非光滑矩阵优化模型，并分析了算法的收敛性。最后，通过大量数值实验表明：在有噪声和无噪声的情况下，所提出的算法都能有效、稳健地分解出低秩–稀疏矩阵。并将提出的算法应用于监控视频的前景和背景分离问题，发现所提出的算法对于该问题有良好的性能，这说明该算法能够解决相关实际问题。

Abstract: In order to achieve robust low-rank sparse matrix decomposition, this paper considers a non-convex and nonsmooth optimization model, in which the ranking function of the matrix is relaxed by Capped-l₁ regularization of the singular values, and l₀ norm of the matrix is relaxed with the l1 norm of the matrix. First, we provide the closed-form thresholding operator for the matrixCapped-l₁ function. Secondly, the alternating direction method of multipliers is proposed to solve our nonconvex and nonsmooth optimization model, and the convergence analysis is provided. Finally, a large number of numerical experiments show that the proposed algorithm can effectively and robustly decompose the low-rank and sparse matrices in the case of noise and noise. The proposed algorithm is applied to the background separation problem of surveillance video, and it is indicated that the proposed algorithm has good performance for this problem, which shows that the algorithm can solve the relevant practical problems.

1. 引言

在大数据时代，随着计算机和信息技术的普及与应用，各种各样的数据信息呈爆炸性增长，时刻都会产生大量的、多样化的、结构复杂的、冗余的、高维的海量数据。研究表明无法通过常规手段直接处理使用这类信息，那么如何从这些高维且冗余的数据中提取有价值的信息便成为大数据科学问题的关键课题之一。大量已有的研究工作表明稀疏性则是研究这一课题的重要手段。

在不同实际应用领域中出现的复杂系统和复杂模型的矩阵，其通常可以具有由低秩分量和稀疏分量组成的特征，而这种复杂系统的可分性为理解复杂系统的行为和性质提供了可能。实现这种矩阵表示的可分性可以描述为如下的矩阵低秩稀疏分解(Low Rank and Sparse Decomposition, LRSD) [1] [2] [3] ：

$\underset{{}_{L,S\in {\text{R}}^{m\times n}}}{\min }rank\left(L\right)+\lambda {\Vert S\Vert }_{{\mathcal{l}}_0},s.t.D=L+S$ , (1)

其中参数λ > 0，rank(·)是矩阵的秩函数， ${\Vert \cdot \Vert }_{l_0}$ 是矩阵的l₀范数，表示矩阵中所有元素的非零个数和，其本质上是为了寻找数据最具价值的低维结构及最佳投影，通过去除数据中的冗余信息，从而找到数据中有价值的信息。

因为LRSD方法克服了主成分分析(Principal Component Analysis, PCA) [4] [5] 方法对非高斯样本或异常值的敏感性在实践中往往使其不够稳健的缺陷，因此该方法又被称为稳定主成分分析法(Robust Principal Component Analysis, RPCA)。LRSD问题的基本出发点在于很多的实际数据矩阵D往往是具有先验信息——近似低秩特性和稀疏特性的。问题(1)中的参数λ则用于平衡矩阵L的低秩程度和矩阵S的稀疏程度，和向量l₀极小化问题一样，问题(1)显然是一个NP-hard的问题，求解的复杂度极高，甚至在实际的应用中可能会出现难以求解的情况，不利于该模型在实际问题中的应用。

为了高效求解LRSD问题，Candès和Li [6] 等提出在一定条件下，最小化l₁范数求得的解等价于最小化l₀范数求得的解，而秩函数则可以通过核范数进行近似表达，该方法即是被称为著名的主成分追踪法(Principal Component Pursuit, PCP)，它的思想是将LRSD的非凸问题进行凸松弛，转化为凸优化问题进行求解。

在求解模型(1)时，PCP方法的出发点在于矩阵的秩等于非零奇异值的个数以及l₁范数是l₀范数的最紧凸松弛，进而将非凸问题(1)进行松弛得到如下最紧凸松弛问题进行求解：

$\underset{{}_{L,S\in {ℝ}^{m\times n}}}{\min }{\Vert L\Vert }_{*}+\lambda {\Vert S\Vert }_{l_1},s.t.D=L+S$ (2)

其中 ${\Vert \cdot \Vert }_{*}$ 表示矩阵奇异值之和，称为矩阵的核范数， ${\Vert \cdot \Vert }_{l_1}$ 表示矩阵所有元素绝对值之和。实际应用中该模型的平衡参数 $\lambda$ 通常设置为 $1/\max \left\{m,n\right\}$ ，m和n分别表示的是矩阵D的行数和列数。

在求解模型(1)时，使用的PCP方法 [6] 会出现对低秩部分和稀疏部分刻画不准确的问题。因此，很多研究者一直在寻求秩函数和稀疏度函数的更加精确的表达方法。在许多经典的LRSD方法中主要是利用核范数对秩函数进行凸近似。虽然核范数已经在低秩矩阵的近似表达中被广泛使用，但是核范数表示的是非零奇异值的和，并不是秩函数的最佳刻画。为了解决该问题，文献 [7] 中提出了截断核范数(Truncated Nuclear Norm, TNN)，实验结果表明该方法在一定程度上能更准确地诱导低秩部分，后续中许多研究基于TNN的方法被广泛应用到低秩稀疏分解中 [8] [9] [10] 。

在求解优化问题(2)时，文献 [11] 基于目标函数的一阶信息提出了迭代阈值算法(Iterative Thresholding, IT)，虽然算法的迭代方式简单也收敛，但其每次迭代都要进行一次奇异值分解且收敛速度很慢，也难以选取合适的步长，无法快速求解大型实际问题。此后，文献 [12] 提出了求解问题(2)的加速临近梯度算法(Accelerated Proximal Gradient, APG)和求解相应对偶问题的梯度上升算法，并通过实验说明这两种算法在处理1000 × 1000维的矩阵时相较于迭代阈值算法加速了50倍。进一步文献 [13] 提出了增广拉格朗日乘子法(Augmented Lagrange Multiplier, ALM)，其中ALM算法相比IT算法和APG算法具有更快的计算速度且所需存储空间更小等优点，在显著提高计算精度的同时其计算速度快于APG算法。然而当目标函数含有两个及以上的变量时，由于ALM 将乘子函数中的所有变量同时最小化，使该算法具有较高的计算复杂度，给求解带来了困难。因此，交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)算法 [14] [15] [16] 应运而生，ADMM算法采用分而治之的思想将不易求解的问题转化为容易求解的子问题进行求解，使其同时兼具了乘子法和交替最小化算法的优点。此外，该算法的复杂度较低，有利于求解，并且该算法具有更高的计算速度，因此受到研究者的广泛关注。

另一方面向量l_1/2正则化理论表明：相较于常用的l₁范数，l_1/2范数可进一步诱导向量的稀疏性，在稀疏信号重建中对噪声具有更强的稳健性。为得到矩阵D更为精确的稀疏低秩表示，有学者将向量的l_1/2范数推广到矩阵，分别用S_1/2范数 [17] [18] (矩阵奇异值构成向量的l_1/2范数)和l_1/2范数来刻画矩阵的秩与稀疏度。与此同时，近年来越来越受到重视的折叠凹正则理论 [19] [20] 表明，相比于凸正则，某些特殊的非凸正则在诱导低秩性和稀疏性方面具有更大的优势。受l_1/2正则化理论的良好表现及拓展，本文将Capped-l₁正则理论应用于矩阵问题中。事实上，我们的数值实验表明了相较于RPCA方法中的核范数正则，Capped-l₁正则可进一步诱导低秩矩阵的低秩性，即拟解决的具体优化模型如下：

$\underset{{}_{L,S\in {\text{R}}^{m\times n}}}{\min }\Phi \left(L\right)+\lambda {\Vert S\Vert }_{l_1},s.t.D=L+S$ (3)

其中， $\Phi \left(L\right)={\displaystyle \underset{i=1}{\overset{\min \{m,n\}}{\sum }}\min }\left\{1,\frac{{\sigma }_i(L)}{\gamma }\right\}$ ， $\gamma$ 是给定的参数， ${\sigma }_i\left(L\right)$ 表示对低秩矩阵L进行奇异值分解(Singular Value Decomposition，SVD)后每一个奇异值所对应的项。

考虑到Capped-l₁模型的目标函数与约束条件关于低秩矩阵与稀疏矩阵是可分的，本文基于文献 [14] 中的交替方向乘子法(Alternating Direction Method of Multipliers, ADMM)算法思想提出交替迭代阈值算法。该算法利用增广Lagrange乘子技术，在迭代过程中采用交替投影的思想逐个更新低秩矩阵、稀疏矩阵和Lagrange乘子。低秩矩阵与稀疏矩阵的更新需要求解两个线性非凸优化子问题，之后通过将作用于向量的Capped-l₁算子推广到矩阵情形，给出其子问题最优解的显式形式，避免每次迭代都要对矩阵进行奇异值分解的弊端，这从很大程度上保证了所设计算法的高精度与低时间代价特性。

与ALM算法相比，大量的模拟实验说明本文所提出的交替阈值迭代算法具有以下优点：达到收敛所需迭代次数与时间代价大幅降低、分解出的低秩矩阵的秩更接近于真实值并且同时算法的可靠性对矩阵L的低秩程度依赖更少。另外，在监控视频背景建模这一实际应用中，交替阈值迭代算法能得到更为稀疏的背景矩阵，具有更为稳健的恢复性能且时间代价相较于ALM算法降幅高达一个数量级，这对实际中海量视频数据的快速处理具有重要意义。

2. 交替方向乘子法

在本节中，我们提出交替方向乘子法来解决问题(3)，并给出该算法的收敛性分析。

2.1. 交替方向乘子法的迭代框架

本为了给出交替方向乘子法的迭代框架，我们首先给出问题(3)的增广拉格朗日函数：

${\mathcal{L}}_{\mu }\left(L,S,Y\right)=\Phi \left(L\right)+\lambda {\Vert S\Vert }_{{\mathcal{l}}_1}+\langle Y,D-L-S\rangle +\frac{\mu }{2}{\Vert D-L-S\Vert }_F^2$ ,

其中 $Y\in R^{m\times n}$ 是Lagrange乘子， $\mu >0$ 表示违反线性约束的惩罚参数。

给定 $\left(L_k,S_k,Y_k\right)$ ，那么用于解问题(3)的交替方向乘子法可以表示为求解如下三个子问题：

$\{\begin{array}{l}{S}_{k+1}=\arg \underset{S}{\min }{\mathcal{L}}_{\mu }\left(L_k,S,Y_k\right)\hfill \\ L_{k+1}=\arg \underset{L}{\min }{\mathcal{L}}_{\mu }\left(L,S_{k+1},Y_k\right)\hfill \\ Y_{k+1}=Y_k+\mu \left(D-L_{k+1}-S_{k+1}\right).\hfill \end{array}$ (4)

很容易可以看出(4)式中的第一个子问题可以表示为如下形式：

$\begin{array}{l}{S}_{k+1}=\arg \underset{S}{\min }\lambda {\Vert S\Vert }_{{\mathcal{l}}_1}+\langle Y_k,D-L_k-S\rangle +\frac{\mu }{2}{\Vert D-L_k-S\Vert }_F^2\\ =\arg \underset{S}{\min }\lambda {\Vert S\Vert }_{{\mathcal{l}}_1}+\frac{\mu }{2}{\Vert S-\left(D-L_k+\frac{1}{\mu }{Y}_k\right)\Vert }_F^2\\ =\arg \underset{S}{\min }\lambda {\Vert S\Vert }_{{\mathcal{l}}_1}+\frac{\mu }{2}{\Vert S-\hat{Y}\Vert }_F^2,\end{array}$ (5)

其中 $\hat{Y}=D-L_k+\frac{\text{1}}{\mu }{Y}_k$ 。显然(4)式问题有如下的闭式解

${\left[S_{k+1}\right]}_{ij}=\text{sign}\left({\hat{Y}}_{ij}\right)\cdot \max \left\{\Vert {\hat{Y}}_{ij}\Vert -\frac{\lambda }{\mu },0\right\}.$ (6)

根据求解(4)中第一个子问题的思想，(4)式中的第二个子问题可以等价的写为

$\begin{array}{l}{L}_{k+1}=\arg \underset{L}{\min }\Phi \left(L\right)+\langle Y_k,D-L-S_{k+1}\rangle +\frac{\mu }{2}{\Vert D-L-S_{k+1}\Vert }_F^2\\ =\arg \underset{L}{\min }\Phi \left(L\right)+\frac{\mu }{2}{\Vert L-\left(D-S_{k+1}+\frac{1}{\mu }{Y}_k\right)\Vert }_F^2\\ =\arg \underset{L}{\min }\Phi \left(L\right)+\frac{\mu }{2}{\Vert L-\bar{Y}\Vert }_F^2,\end{array}$ (7)

其中 $\bar{Y}=D-S_{k+1}+\frac{1}{\mu }{Y}_k$ ，那么可得到问题(7)的解

$L_{k+1}={\mathbb{T}}_{Capped{\mathcal{l}}_1}\left(\bar{Y}\right):=U{T}_{Capped{\mathcal{l}}_1}\left(\Sigma \right)V^{\top }$ , (8)

这里 $U\Sigma V^{\top }=\bar{Y}$ 是 $\bar{Y}$ 的奇异值分解， $T_{Capped{\mathcal{l}}_1}\left(\Sigma \right)$ 是矩阵 $\Sigma$ 的阈值算子，即

$T_{Capped{\mathcal{l}}_1}{\left(\Sigma \right)}_{ii}=\{\begin{array}{ll}\max \left\{{\Sigma }_{ii}-\frac{1}{\gamma \mu },0\right\},\hfill & {\Sigma }_{ii}\le \gamma +\frac{1}{2\gamma \mu },\hfill \\ {\Sigma }_{ii},\hfill & {\Sigma }_{ii}>\gamma +\frac{1}{2\gamma \mu }.\hfill \end{array}$ (9)

上述交替方向乘子法的关键是在每次迭代中交替更新低秩矩阵、稀疏矩阵和Lagrange乘子，直到满足算法的收敛条件。因此，算法整体的计算精度与时间代价在很大程度上取决于式(4)中两个子问题的求解。(6)与(8)给出了(4)中两个子问题的的显式解，因此我们提出了如下交替方向乘子法解问题(3)：

2.2. 收敛性分析

本小结给出算法的收敛性分析，针对算法(2.1)有如下结论：

定理2.1 令 $\left\{\left(L_k,S_k,Y_k\right)\right\}$ 是由ADMM算法生成的迭代序列，则以下结论成立：

i) 序列 $\left\{\left(L_k,S_k,Y_k\right)\right\}$ 是有界的；

ii) $\underset{k\to \infty }{\lim }{\Vert S_{k+1}-S_k\Vert }_F=0,\underset{k\to \infty }{\lim }{\Vert L_{k+1}-L_k\Vert }_F=0$ ；

iii) $\underset{k\to \infty }{\lim }{\Vert D-S_{k+1}-L_{k+1}\Vert }_F=0$ ，且 $\left\{\left(L_k,S_k,Y_k\right)\right\}$ 的聚点是问题的可行解。

证明. i) 令 $U_k{\Lambda }_k{V}_k^{\top }$ 为矩阵 ${\bar{Y}}_k:=D-S_{k+1}+\frac{1}{{\mu }_k}{Y}_k$ 在 $k+1$ 次迭代中的奇异值分解，根据 $L_{k+1}$ 在(8)中的定义，有

$L_{k+1}=U_k{T}_{Capped{\mathcal{l}}_1}\left({\Lambda }_k\right)V_k^{\top }.$ (11)

再由(10)中的第三个等式和(11)，可得

$\begin{array}{l}{\Vert Y_{k+1}\Vert }_F={\Vert Y_k+{\mu }_k\left(D-L_{k+1}-S_{k+1}\right)\Vert }_F\\ ={\mu }_k{\Vert \frac{1}{{\mu }_k}{Y}_k+D-L_{k+1}-S_{k+1}\Vert }_F\\ ={\mu }_k{\Vert U_k{\Lambda }_k{V}_k^{\top }-U_k{T}_{Capped{\mathcal{l}}_1}\left({\Lambda }_k\right)V_k^{\top }\Vert }_F\\ ={\mu }_k{\Vert {\Lambda }_k-T_{Capped{\mathcal{l}}_1}\left({\Lambda }_k\right)\Vert }_F\\ \le \frac{\sqrt{m}}{\gamma }<\infty ,\end{array}$

这里 $T_{Capped{\mathcal{l}}_1}(\cdot )$ 定义如(9)式所示，因此 $\left\{Y_k\right\}$ 是有界的。

接下来，我们考虑序列 $\left\{S_k\right\}$ 的有界性。由(10)，我们得到

$\mathcal{L}\left(L_{k+1},S_{k+1},Y_k,{\mu }_k\right)\le \mathcal{L}\left(L_{k+1},S_k,Y_k,{\mu }_k\right)\le \mathcal{L}\left(L_k,S_k,Y_k,{\mu }_k\right),$ (12)

联合迭代公式 $Y_{k+1}=Y_k+{\mu }_k\left(D-L_{k+1}-S_{k+1}\right)$ ，可得

$\begin{array}{l}\mathcal{L}\left(L_{k+1},S_{k+1},Y_k,{\mu }_k\right)\le \mathcal{L}\left(L_k,S_k,Y_k,{\mu }_k\right)\\ =\mathcal{L}\left(L_k,S_k,Y_{k-1},{\mu }_{k-1}\right)+\langle Y_k-Y_{k-1},D-L_k-S_k\rangle +\frac{{\mu }_k-{\mu }_{k-1}}{2}{\Vert D-L_k-S_k\Vert }_F^2\\ =\mathcal{L}\left(L_k,S_k,Y_{k-1},{\mu }_{k-1}\right)+\frac{{\mu }_k-{\mu }_{k-1}}{2}{\Vert D-L_k-S_k\Vert }_F^2+\langle Y_k-Y_{k-1},\frac{1}{{\mu }_{k-1}}\left(Y_k-Y_{k-1}\right)\rangle \\ =\mathcal{L}\left(L_k,S_k,Y_{k-1},{\mu }_{k-1}\right)+\frac{{\mu }_k+{\mu }_{k-1}}{2{\mu }_{k-1}^2}{\Vert Y_k-Y_{k-1}\Vert }_F^2\\ =\mathcal{L}\left(L_k,S_k,Y_{k-1},{\mu }_{k-1}\right)+\frac{\rho +1}{2{\mu }_{k-1}}{\Vert Y_k-Y_{k-1}\Vert }_F^2.\end{array}$ (13)

通过(12)、(13)和 $\rho >1$ ，立即可得

$\mathcal{L}\left(L_{k+1},S_{k+1},Y_k,{\mu }_k\right)\le \mathcal{L}\left(L_1,S_1,Y_0,{\mu }_0\right)+\frac{\left(\rho +1\right)\Theta }{2{\mu }_0}{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\left(\frac{1}{\rho }\right)}^{k-1}}<\infty ,$

这里 $\Theta$ 是 ${\Vert Y_k-Y_{k-1}\Vert }_F^2$ 的上界。上式也表明 $\mathcal{L}\left(L_{k+1},S_{k+1},Y_k,{\mu }_k\right)$ 是有上界的。另外我们有

$\begin{array}{l}\Phi \left(L_k\right)+\lambda {\Vert S_k\Vert }_{{\mathcal{l}}_1}=\mathcal{L}\left(L_k,S_k,Y_{k-1},{\mu }_{k-1}\right)-\langle Y_{k-1},D-L_k-S_k\rangle -\frac{{\mu }_{k-1}}{2}{\Vert D-L_k-S_k\Vert }_F^2\\ =\mathcal{L}\left(L_k,S_k,Y_{k-1},{\mu }_{k-1}\right)+\langle Y_{k-1},\frac{1}{{\mu }_{k-1}}\left(Y_k-Y_{k+1}\right)\rangle -\frac{1}{2{\mu }_{k-1}}{\Vert Y_k-Y_{k-1}\Vert }_F^2\\ =\mathcal{L}\left(L_k,S_k,Y_{k-1},{\mu }_{k-1}\right)-\frac{1}{2{\mu }_{k-1}}\left({\Vert Y_k\Vert }_F^2-{\Vert Y_{k-1}\Vert }_F^2\right)<\infty .\end{array}$ (14)

因为 ${\Vert S_k\Vert }_{{\mathcal{l}}_1}$ 是具有强制性的，即 $\underset{S\to \infty }{\lim }{\Vert S\Vert }_{{\mathcal{l}}_1}=+\infty$ ，且 $\Phi \left(L_k\right)$ 非负的，因此由(14)可得到序列 $\left\{S_k\right\}$ 有界。

最后考虑序列 $\left\{L_k\right\}$ 的有界性。特别地，由 ${\mu }_k$ 的更新准则知 $\underset{k\to +\infty }{\lim }{\mu }_k=+\infty$ ，以及 $\left\{Y_k\right\}$ 的有界性，因此有如下结果

$\underset{k\to \infty }{\lim }{\Vert D-L_{k+1}-S_{k+1}\Vert }_F=\underset{k\to \infty }{\lim }\frac{1}{{\mu }_k}{\Vert Y_{k+1}-Y_k\Vert }_F=0,$ (15)

此外还有

$\begin{array}{l}{\Vert L_{k+1}\Vert }_F={\Vert D-S_{k+1}-\left(D-L_{k+1}-S_{k+1}\right)\Vert }_F\\ \le {\Vert D\Vert }_F+{\Vert S_{k+1}\Vert }_F+{\Vert D-L_{k+1}-S_{k+1}\Vert }_F.\end{array}$ (16)

那么由(15)、(16)以及 $\left\{S_{k+1}\right\}$ 的有界性，可知 $\left\{L_{k+1}\right\}$ 有界。综上可得序列 $\left\{\left(L_k,S_k,Y_k\right)\right\}$ 有界。

ii) 我们首先证明 $\underset{k\to +\infty }{\lim }{\Vert S_{k+1}-S_k\Vert }_F=0$ 。由(10)的第三个更新准则以及(5)可知

$\begin{array}{l}\underset{k\to \infty }{\lim }{\Vert S_{k+1}-S_k\Vert }_F=\underset{k\to \infty }{\lim }{\Vert S_{k+1}-\left(D-L_k-{\mu }_{k-1}^{-1}{Y}_k+{\mu }_{k-1}^{-1}{Y}_{k-1}\right)\Vert }_F\\ =\underset{k\to \infty }{\lim }{\Vert S_{k+1}-\left(D-L_k+{\mu }_k^{-1}{Y}_k\right)-\left({\mu }_{k-1}^{-1}{Y}_{k-1}-{\mu }_k^{-1}{Y}_k-{\mu }_{k-1}^{-1}{Y}_k\right)\Vert }_F\\ \le \underset{k\to \infty }{\lim }{\Vert S_{k+1}-\left(D-L_k+{\mu }_k^{-1}{Y}_k\right)\Vert }_F+{\Vert {\mu }_{k-1}^{-1}{Y}_{k-1}-{\mu }_k^{-1}{Y}_k-{\mu }_{k-1}^{-1}{Y}_k\Vert }_F\\ \le \underset{k\to \infty }{\lim }\left[{\left({\displaystyle \underset{i,j}{\sum }{\left|{\left[S_{k+1}\right]}_{ij}-{\left[D-L_k+{\mu }_k^{-1}{Y}_k\right]}_{ij}\right|}^2}\right)}^{1/2}+{\Vert {\mu }_{k-1}^{-1}{Y}_{k-1}-{\mu }_k^{-1}{Y}_k-{\mu }_{k-1}^{-1}{Y}_k\Vert }_F\right]\\ \le \underset{k\to \infty }{\lim }\left[\frac{\lambda \sqrt{mn}}{{\mu }_k}+{\mu }_{k-1}^{-1}{\Vert Y_k-Y_{k-1}\Vert }_F+{\mu }_k^{-1}{\Vert Y_k\Vert }_F\right]\\ =0,\end{array}$ (17)

这里最后等式成立是因为 ${\Vert Y_k-Y_{k-1}\Vert }_F$ 和 ${\Vert Y_k\Vert }_F$ 有界且 $\underset{k\to +\infty }{\lim }{\mu }_k=+\infty$ 。再由(10)的第三个更新准则以及(8)、(9)和(11)可知

$\begin{array}{l}\underset{k\to \infty }{\lim }{\Vert L_{k+1}-L_k\Vert }_F=\underset{k\to \infty }{\lim }{\Vert L_{k+1}-\left(D-S_k+{\mu }_{k-1}^{-1}{Y}_{k-1}-{\mu }_{k-1}^{-1}{Y}_k\right)\Vert }_F\\ =\underset{k\to \infty }{\lim }{\Vert {\mathbb{T}}_{Capped\mathcal{l}1}\left(D-S_{k+1}+{\mu }_k^{-1}{Y}_k\right)-\left(D-S_{k+1}+{\mu }_k^{-1}{Y}_k\right)-\left(S_{k+1}-S_k\right)-\left({\mu }_{k-1}^{-1}{Y}_{k-1}-{\mu }_{k-1}^{-1}{Y}_k-{\mu }_k^{-1}{Y}_k\right)\Vert }_F\\ \le \underset{k\to \infty }{\lim }{\Vert {\Lambda }_k-T_{Capped{\mathcal{l}}_1}\left({\Lambda }_k\right)\Vert }_F+{\Vert S_{k+1}-S_k\Vert }_F+{\mu }_k^{-1}{\Vert Y_k\Vert }_F+{\mu }_{k-1}^{-1}{\Vert Y_k-Y_{k-1}\Vert }_F\\ \le \underset{k\to \infty }{\lim }\frac{m}{\gamma {\mu }_k}+{\Vert S_{k+1}-S_k\Vert }_F+{\mu }_k^{-1}{\Vert Y_k\Vert }_F+{\mu }_{k-1}^{-1}{\Vert Y_k-Y_{k-1}\Vert }_F\\ =0.\end{array}$ (18)

最后由式子(15)、(17)和(18)可知结论ii)成立。

iii) 由(i)可知，因为序列 $\left\{\left(L_k,S_k,Y_k\right)\right\}$ 有界，所以存在聚点 $\left(L^{\star },S^{\star },Y^{\star }\right)$ 和一个收敛子序列 $\left(L_{k_j},S_{k_j},Y_{k_j}\right)$ 使得 $\underset{j\to +\infty }{\lim }\left(L_{k_j},S_{k_j},Y_{k_j}\right)=\left(L^{\star },S^{\star },Y^{\star }\right)$ ，根据(10)式中的第三个等式，可知

$L_{k_j+1}+S_{k_j+1}-D=\frac{1}{{\mu }_{k_j}}\left(Y_{k_j}-Y_{k_{j+1}}\right)$ (19)

于是令 $j\to +\infty$ ，有 $L^{\star }+S^{\star }-D=\frac{1}{{\mu }^{\star }}\left(Y^{\star }-Y^{\star }\right)=0$ ，故聚点为问题的可行解。

3. 数值实验

本节我们将对所提出的ADMM算法与以下三种算法进行比较：Augmented Lagrange Mutiplier (ALM)算法 [13] ，MoG [21] 算法和Weighted Nuclear Norm Minimization (WNNM) [22] 算法。对于待分解的矩阵 $D\in {\text{R}}^{m\times m}$ ，用矩阵中非零元素的比例(记作pe)来刻画其稀疏成分S的稀疏程度，用矩阵秩r与维数m的比值(记作pr)来刻画其低秩成分L的低秩程度。我们采用与相关研究 [6] [12] [23] 似的模式来生成矩阵D。

对于三种比较算法的参数，我们依然选取他们原始的取值。例如ALM算法的原始参数 $\rho =1.1$ ， $\alpha =1$ ， $\beta =0.2$ 。MoG算法中的参数 ${\mu }_0=0$ ， ${\beta }_0=1\text{e}-6$ ， ${\alpha }_0=1\text{e}-6$ 。WNNM算法的参数 $\lambda =1/\sqrt{m}$ ， $\rho =1.05$ 。对于我们的ADMM算法，设置参数 $\rho =1.1$ ， $\gamma =0.25$ ， $\lambda =1/\sqrt{m}$ ， $\text{maxiter}=1000$ ， $xtol=1\text{e}-7$ 。

我们算法的所有结果都是在台式电脑(CPU为3.40 GHz，内存为8.00 GB)上使用软件Matlab R2018b完成的。

3.1. 随机实验模拟

本节将在有、无噪声干扰的情况下，比较ALM、MoG、WNNM和ADMM这四种算法实现稀疏–低秩矩阵的精度与速度，并研究算法对于低秩成分的低秩程度与稀疏成分的稀疏程度的稳健性。

3.1.1. 无噪声情况下的实验结果

在本结中，首先生成待分解矩阵 $D\in {\text{R}}^{m\times m}$ ，具体生成如下：1) 独立生成随机矩阵U， $V\in {\text{R}}^{m\times r}$ ，这里 $r=pr\times m$ ， $U=randn(m,r)$ 和 $V=randn\left(m,r\right)$ 。令 $L=U{V}^{\prime }$ ，得到秩为r的低秩矩阵。2) 均匀随机选取稀疏矩阵 $S\in {\text{R}}^{m\times m}$ 的 $pe\times m^2$ 个非零元的位置，这些位置上元素的取值独立服从[0, 1]区间上的均匀分布。3) 令 $D=L+S$ ，得到待分解矩阵D。其次，设置 $m=500:500:3000$ ， $pr=0.01$ ， $pe=0.05$ 。对于以上问题，我们运行10次并记录以下结果：算法达到收敛所需的时间(CPU Time)、迭代数(Iterations)和相对误差，其中相对误差的定义如下：

$\text{rel\_err}L=\frac{{\Vert L-L^{*}\Vert }_F}{{\Vert L\Vert }_F},\text{rel\_err}S=\frac{{\Vert S-S^{*}\Vert }_F}{{\Vert S\Vert }_F}.$

计算结果见表1和图1所示。

Table 1. The numeric results of ALM, MoG, WNNM and ADMM algorithms for sparse low-rank matrix factorization problems of different scales (σ = 0)

表1. ALM，MOG，WNNM和ADMM算法对不同规模的稀疏低秩矩阵分解问题的数值结果(σ = 0)

由表1可以看出：在无噪声情况下，ADMM算法虽然Iterations高于ALM和MoG算法，但是ADMM算法的rel_errL、rel_errS和CPU Time都是小于其他算法的，并且随着矩阵维数m，n的增加，同样可以得到ALM与MoG算法比ADMM算法的rel_errL、rel_errS和CPU Time指标值高，即ADMM算法分解得到的rel_errL、rel_errS、Iterations都优于ALM、MoG算法。对于WNNM算法而言，无论是rel_errL、rel_errS、Iterations和CPU Time都高于ADMM算法。因此，ADMM算法总体上来看优于其他三个算法，能够准确地分解稀疏–低秩矩阵。

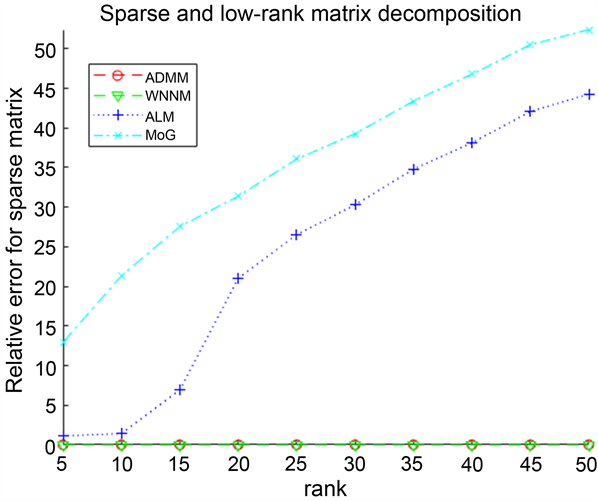rel_errL rel_errS 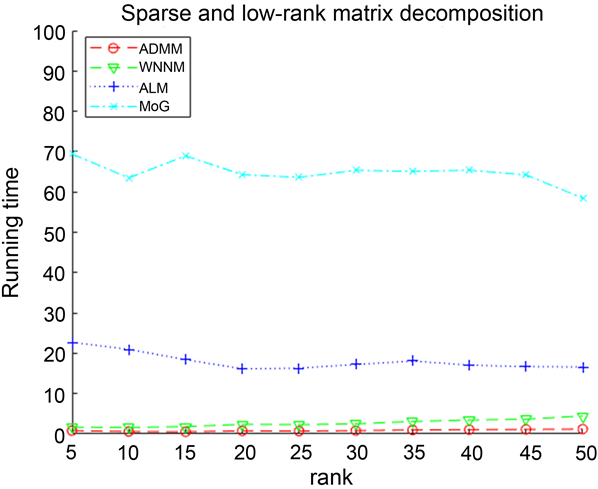Iterations CPU Time

Figure 1. The numeric results for sparse low-rank matrix factorization problems of different scales (σ = 0)

图1. 对不同规模的稀疏低秩矩阵分解问题的数值结果(σ = 0)

图1记录了四个算法在无噪声情况下，对维度为 $m=n=500$ ， $pe=0.05$ ， $r=5:5:50$ 的稀疏–低秩矩阵分解的实验结果。从计算精度上来看，MoG、ALM算法分解出的稀疏–低秩矩阵精度较低相对误差较大，并且随着r的不断增大，其分解结果的相对误差也呈现出比较大的递增趋势，而本文的ADMM算法分解效果不仅准确，而且也比较稳定。从计算效率上来看，MoG算法的Iterations和CPU Time比其他几种算法都多，并且ALM、WNNM算法的效率也不高，但是对于ADMM算法而言，随着r的不断增大，它不仅能够准确地分解稀疏–低秩矩阵，而且具有较好的稳定性，综上ADMM算法要比WNNM、ALM和MoG算法能够快速地、精确地分解稀疏低秩矩阵。因此ADMM算法在无噪声情况下是优于其他算法的。

3.1.2. 有噪声情况下的实验结果

待分解矩阵含噪声的情况下数值结果如表2和图2所示。

Table 2. The numeric results of ALM, MoG, WNNM and ADMM algorithms for sparse low-rank matrix factorization problems of different scales (σ = 0)

表2. ALM，MOG，WNNM和ADMM算法对不同规模的稀疏低秩矩阵分解问题的数值结果(σ = 0)

由表2可以看出：在有噪声的情况下，ADMM算法在时间上慢于MoG算法，但是MoG算法不能够成功分解稀疏–低秩矩阵，其中对于ALM算法来说，虽然Iterations比ADMM算法低，但是ALM算法的CPU Time比ADMM高出一个数量级，并且其计算精度远不如ADMM算法。对于WNNM算法，通过表中数据看出，ADMM算法与WNNM算法在计算精度和Iterations相差不是很大，但是可以明显得到WNNM算法的CPU Time比ADMM算法的所需时间长得多，其次分解得到的低秩矩阵与原始矩阵的误差虽然大于WNNM算法，但是得到的稀疏矩阵要更近似原始的稀疏矩阵，并优于其他两个算法。因此，ADMM算法具有更加准确和稳健地分解稀疏–低秩矩阵的性能，且优于其他三种算法。因此我们的算法有能更稳健的恢复性能。

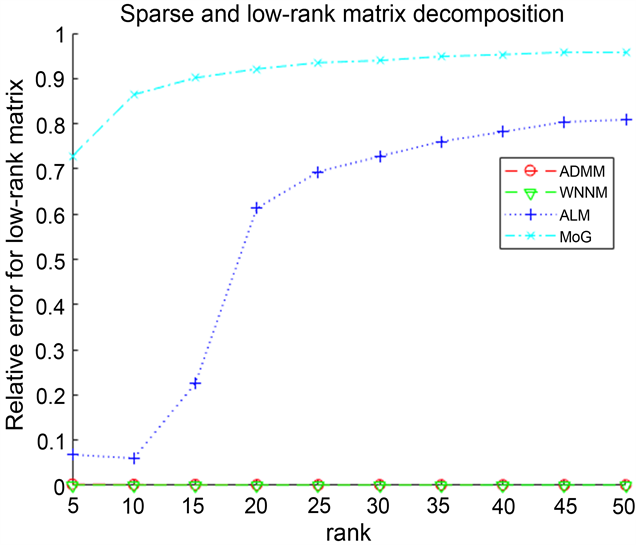
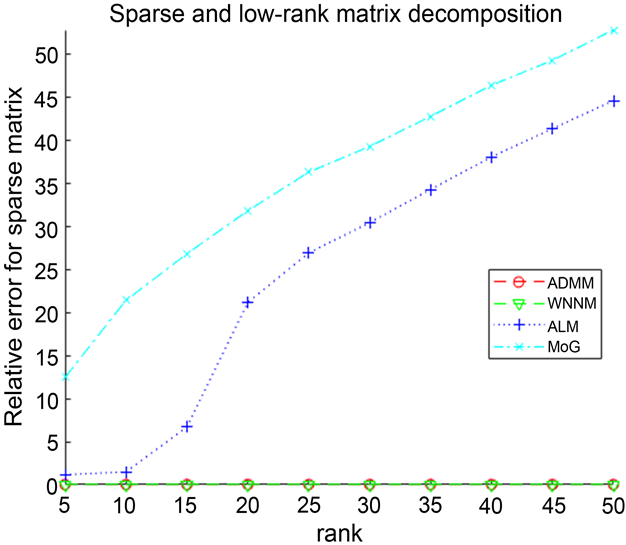rel_errL rel_errS 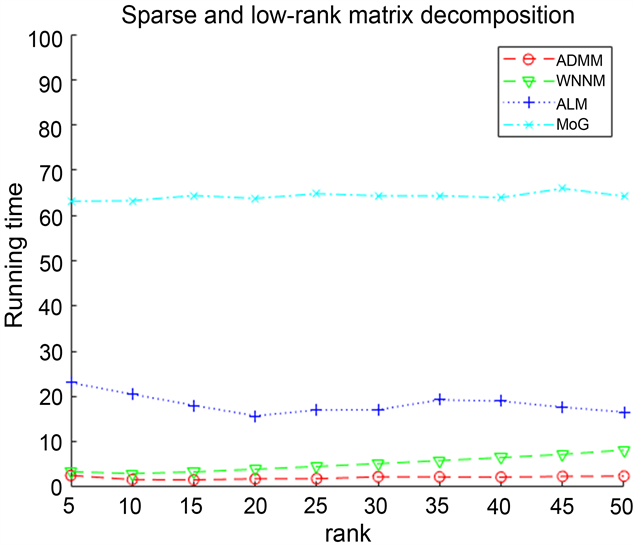Iterations CPU Time

Figure 2. The numeric results for sparse low-rank matrix factorization problems of different scales (σ = 0.01)

图2. 对不同规模的稀疏低秩矩阵分解问题的数值结果(σ = 0.01)

图2记录了四个算法在有噪声情况下，对维度为 $m=n=500$ ， $pe=0.05$ ， $r=5:5:50$ 的稀疏–低秩矩阵分解的实验结果。由图同样可以看出，提出的ADMM算法在迭代数上多于ALM，但比其他算法速度快并且更能精确的分解稀疏低秩矩阵。总之，可以得到我们所提出的算法在有无噪声的情况下，都能有效、稳健地分解稀疏–低秩矩阵。

3.2. 监控视频应用

在监控视频应用中，最重要的环节是对视频进行背景消除。首先我们从文献 [24] 的12R数据集中选取视频，详情如下：

· Campus该视频包含80个240 × 320的视频帧；

· Lobby该视频包含80个128 × 160的视频帧；

· Escalator该视频包含80个128 × 160的视频帧；

其次，为了定量评估背景消除的结果，我们使用基于四个量的度量：TP、TN、FP和FN，其中TP是为正确分类为正数的总数——即前景像素被正确分类为前景；TN是为正确分类为负数的总数——即背景像素被正确分类为背景；FN是错误分类为负数的总数——即前景像素被错误地分类为背景；FP是错误分类为正数的总数——即背景像素被错误地分类为前景。那么可得到recall，precision和F-measure三个指标，如下所示：

$\text{recall}=\frac{\text{TP}}{\text{TP+FN}},\text{precision}=\frac{\text{TP}}{\text{TP+FP}},\text{F-measure}=\text{2}\frac{\text{recall*precision}}{\text{recall}+\text{precision}}.$

我们再记录每个算法使用的时间，那么可以说一个更高的召回率、精度和F-度量值以及更少的时间代表更好的算法性能。最后，所有算法的参数取值依然和随机实验部分一样并将结果展现在表3和图3中。

Table 3. The numeric results of all the compared algorithm

表3. 所有比较算法的数值结果

由表3可以看出，我们算法在对视频进行背景消除实验中，所需要的时间最短，而且几乎比WNNM、ALM、MoG算法有更高的precision，recall，F-measure值。因此，我们的ADMM算法比其他算法处理前景背景分离更有优势。

Figure 3. Experimental results on background subtraction

图3. 背景消除的数值结果

由图3中的结果表明，我们所提出的算法相比于其他三种算法可以更有效、清晰地分离背景和前景。因此，我们的算法要比其他算法更具优势。

4. 总结

本文将研究向量稀疏优化中的Capped-l₁正则松弛理论拓展到矩阵问题中，进而提出了可适用于矩阵问题的Capped-l₁阈值算子，并将其应用于非凸非光滑优化模型。首先，我们在交替方向乘子法框架下求解该模型，并证明我们所提出的算法具有稳定的可行解。其次，通过大量的数值模拟实验表明：与其他算法相比，无论是在有噪声还是无噪声的情况下，我们的算法都能够快速准确地分解出低秩–稀疏矩阵。特别地，在有噪声的情况下，我们的算法还具有较强的稳健性。最后，我们成功地将这种新算法应用于监控视频背景建模这一实际问题，并且也验证了在处理实际问题时我们的算法能够进行很好地背景消除。

基金项目

国家自然科学基金项目(12261020)；贵州省科技计划项目(ZK [2021] 009)；贵州大学SRT项目(贵大SRT字(2022) 461号)。

NOTES

^*通讯作者。