1. 引言
奥陌陌(Oumuamua) [1] - [18] 是已知的第一颗经过太阳系的星际天体。2017年10月19日,被科学家们发现,当时距离地球大约3000万公里。图1为奥陌陌的运行轨道示意图。Oumuamua直径在百米级,以每秒26公里左右的速度从天琴座方向冲进太阳系,近乎与黄道面垂直。呈现一个雪茄状,大约长400米,宽40米,颜色偏红,具有固态表面,但是不能区分是岩石或金属构成。是人类首次在太阳系内发现系外天体。
按照现有的观测和计算结果,此天体在2017年的9月9日达到了近日点,近日点距离太阳0.25个天文单位,在以大约每秒40公里的速度离开太阳系。在11月1日,经过了火星轨道上空。
在只受引力的影响时,小行星会严格遵循由引力计算出的轨迹运行。但观测到的数据表明,直到2018年1月2日,奥陌陌的位置与计算出的轨道存在4万公里的偏差(2018年5月3日差值达到10万公里)。因此需要加入一个非引力加速度来解释其运行轨迹。
由以上资料可以得到:奥陌陌以26.3 km/s的速度进入太阳系,近日点距离0.2559个天文单位(3.828 × 1011 m),奥陌陌通过近日点以后轨道明显偏离双曲线轨道,奥陌陌离开太阳系的速度会超过40 km/s。
2. 偏转引力理论简述(引力线在偏转物体运动方向)
偏转引力理论 [19] [20] (引力线在偏转物体运动方向)发表于《天文与天体物理》Vol. 10 No. 2 (April 2022),简述如下:星球由物质够成,物质由分子够成,分子由原子够成,原子由原子核和电子够成,电子质量太小,这里暂不考虑,原子核由质子和中子够成,这里把质子和中子统称为核子,物体的质量与核子数量基本成比例,因此可以把核子作为质量的基本单位考虑。核子发射引力子,星球巨量的核子向四面八方发射大量的引力子,大量引力子以波(这里称为引力能量波)的形式传播形成引力线,星球周围的引力线组合形成引力场,引力子遇到处在引力场中的其它物体,引力子被其它物体的核子吸收,形成引力,这就是引力的传递过程。这里为了便于叙述,把中心物体称为“星球”,把处在星球引力场中的物体称为“物体”。
图2是运动物体q在星球p的引力场中的运行情况,我们把星球和物体都看成质点,p1、p2是星球p从其中心p0发出的两条相邻引力线,物体q沿图中q方向运行。
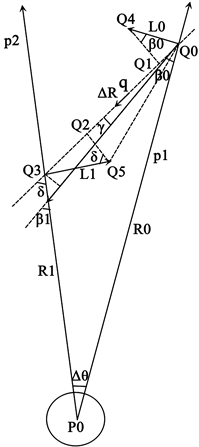
Figure 2. Analysis of objects running between gravitational lines
图2. 物体在引力线之间运行分析
对于星球,包含的核子数量与星球质量成正比,假设每个核子在引力线一个周期内发出一个核子,在单位时间内发出ng个引力子,星球内部的核子发出的引力子与星球内部其它核子发生作用,形成星球内部的引力,将星球物质聚集在一起,星球内部靠近外表层的核子,发出的引力子向星球外部发射,设星球发射到星球外部的引力子数量与星球核子发出的引力子总数的比例为k1,星球质量为m1,中子质量为m0,这样星球单位时间发往外部的引力子数量为:
(1)
设星球引力线之间的夹角为Δθ,星球发出的引力子与距离R处质量为m2的物体相遇的核子数量为:
(2)
设星球发出的引力子与单个核子作用的系数为kR,单条引力线上的引力子与引力场中物质作用的时间为Δt,一般的单个核子单位时间吸收引力子数量应该与单位时间发射引力子数量相等,设为ng,引力子穿透物体m2表层可以达到与物体内部核子发生作用的引力子比例为k2,则星球与物质发生作用的引力子数量为:
(3)
星球发出的引力子形成引力线,引力线以波的形式传播,引力能量波的振幅垂直于引力线传播方向,所以引力子与距离R处的核子相遇,产生的位移垂直于引力线方向,物体产生的位移的平方与引力子交换的能量成正比,设单个引力子与单个核子交换的能量为普朗克常数,而整个物体位移的平方与物质质量成反比,所以星球发出的引力子与物体相遇时,物体产生的位移为:
(4)
设:
(5)
引力子与物体m2作用的时间Δt由物体通过两条引力线之间的距离ΔR和物体通过引力线时的速度v决定,这样公式(4)可以简化为:
(6)
图2中,设物体与星球初始距离为R0,物体运动方向与星球引力线的初始夹角为β0,物体的在Q1点的运行速度为v0,引力线之间的夹角为Δθ,物体与引力线p1作用形成的位移为L0,物体与引力线p2作用形成的位移为L1,物体运行到引力线p2处时,与星球的预期距离为R01,物体在引力线之间的运动距离为ΔR,物体受前后引力线作用最后形成的运动方向偏转角为γ,物体的在Q3点的运行速度为v1,则有:
(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
根据力矩原则,物体在Q3点的垂直位移Δq⊥为:
(16)
(17)
设物体初始速度为V0,物体受L0//影响,速度加速到V01:
(18)
物体受L1//影响,速度减速速到V1:
(19)
(20)
(21)
(22)
为了物体运动方向与引力线夹角超过90˚后公式的一致,这里将
转换为
:
(23)
(24)
(25)
设物体从引力线p1运行到引力线p2后,形成新的物体与星球距离为R1,物体运动方向与星球引力线的夹角为β1:
(26)
(27)
(28)
3. 奥陌陌轨道偏离的原因:太阳斥力
为了解释奥陌陌轨道偏离问题,现在我们先看看当物体运行方向与星球引力线的夹角超过90˚的情况,图3中,引力线与物体的作用力在Q0点朝下,在Q3点朝上,作用力的合力朝远离星球的方向,此时星球引力线对物体的作用不是引力而是斥力,奥陌陌在进入太阳系时,它的运行方向和太阳引力线的夹角是小于90˚的,随着奥陌陌与太阳的距离越来越近,这个夹角也在逐步增大,当到近日点时这个夹角等于90˚,随后随着奥陌陌继续运行,这个夹角超过90˚,此时奥陌陌受到太阳引力线的作用如图3所示,太阳引力线对奥陌陌的作用背向太阳,它不再是引力而是斥力。这就形成了奥陌陌实际轨道与我们按引力理论计算轨道的偏差的原因。
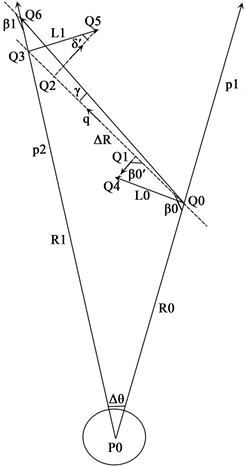
Figure 3. The repulsive force of the planet
图3. 星球的斥力
4. 奥陌陌运行轨道模拟
根据以上推导,可以对奥陌陌绕太阳运行轨道进行模拟,表1是数据模拟的部分截图,表1中引力线夹角为0.002弧度,太阳的质量:1.989E30 kg (这里E为以10为底的指数,1.989E30 kg为1.989 × 1030 kg,以下类似),奥陌陌等效半径r2取70 m,由于笔者笔记本电脑精度的限制,奥陌陌与太阳起始距离R取7.84E10 m,奥陌陌运行方向与引力线夹角为83˚ (1.44862弧度),单个核子单位时间发射引力子数量,太阳发射到球外引力子比例,引力子与核子发生作用的比例,引力子穿透物体表层与核子发生作用的比例,核子吸收引力子的比例,这几个因素的综合因数ng * (k1 * kR * k2)0.5为:6.02636017014540E−20,奥陌陌进入太阳系的角度取0.785弧度(45˚),数据模拟中,奥陌陌初始速度为26.3 km,奥陌陌运行方向与引力线夹角β为90˚时,奥陌陌到达近日点距离为:3.82848E10 m (0.256天文单位),速度为41,212 m,奥陌陌运行方向与引力线夹角超过90˚时,偏转角γ出现负值,奥陌陌运行方向与引力线夹角β为1.63202弧度(93.555˚)时,奥陌陌加速度达到峰值为:5.403 m/s2,此时速度为41,358 m/s,奥陌陌运行方向与引力线夹角β为3.12863弧度(179.3˚)时,奥陌陌模拟速度为42,103 km/s。

Table 1. Partial data of Oumuamua’s trajectory simulation
表1. 奥陌陌运行轨迹模拟部分数据
图4是奥陌陌绕太阳运行轨道数据模拟效果图。由图可以看出,奥陌陌图4是奥陌陌运行轨迹数据模拟效果图,由图可以看出奥陌陌运行轨迹并非一个标准的双曲线,而是经过近日点后有一个加速偏离。
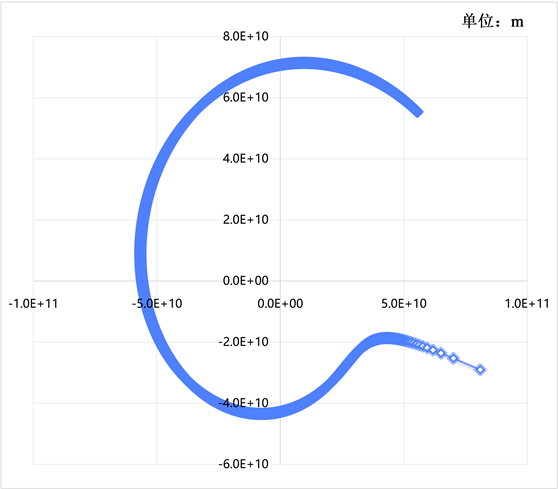
Figure 4. Simulation effect diagram of Oumuamua’s orbit data
图4. 奥陌陌运行轨道数据模拟效果图
图5是奥陌陌速度模拟效果图。由图可以看出,奥陌陌进入太阳系后一直在加速,即使在近日点之后,奥陌陌任然在加速。
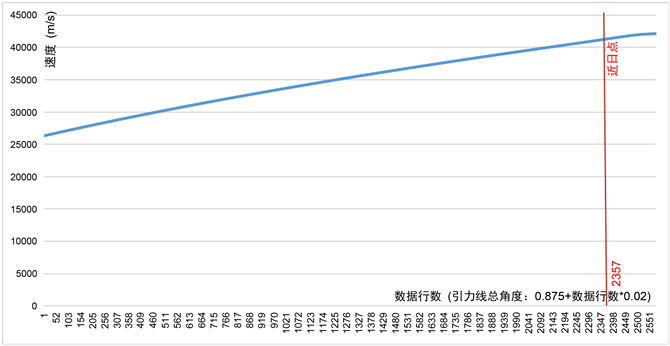
Figure 5. Oumuamua speed change curve
图5. 奥陌陌速度变化曲线
图6是奥陌陌加速度变化模拟效果图,由图可以看出:奥陌陌在到达近日点之前,加速度在减小,接近近日点时加速度开始变大,过近日点之后,在93˚会出现一个峰值,然后加速度减小,但是速度还在增加。
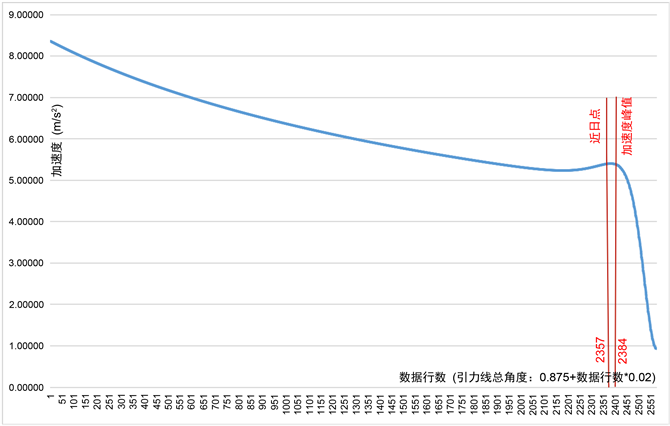
Figure 6. Oumuamua acceleration change curve
图6. 奥陌陌加速度变化曲线
5. 讨论
奥陌陌轨道模拟过程中,综合位移需要进一步细化,由于没有奥陌陌很详细的观测资料,本文的模拟只能算是一个原理性模拟,与奥陌陌实际运行轨道会有一定出入。
6. 结论
物质由核子(中子和质子的统称)够成,核子发出引力子,在空间形成引力线,引力线以波的形式传播形成引力场,处在引力场中的核子与引力能量波共振吸收引力子形成引力。奥陌陌在太阳引力场中运行,受太阳引力线的作用,会产生垂直于太阳引力线方向的位移,当奥陌陌运行在两条太阳引力线中间时,受到前后两条引力子作用的位移和方向不一样,这两个位移垂直于物体运动方向的分量会影响奥陌陌的运行方向,平行于奥陌陌运动方向的分量会影响奥陌陌的运行速度。根据力矩作用原理,两条引力线产生的位移垂直于奥陌陌运动方向的分量的合力矩会使奥陌陌产生一个垂直于奥陌陌运动方向的位移。当奥陌陌刚进入太阳系时,其运动方向与太阳引力线的夹角很小,引力线使奥陌陌产生的位移会使奥陌陌向太阳偏转,随着奥陌陌与太阳距离的变化,其运动方向与引力线的夹角会逐渐变大,当奥陌陌运行到近日点时,奥陌陌运动方向与引力线夹角等于90˚,随后随着奥陌陌的继续运行,奥陌陌运动方向与引力线夹角大于90˚,奥陌陌的前后引力线对奥陌陌作用的合力矩产生的位移背向太阳方向,此时太阳的引力线对奥陌陌产生的作用不是引力,而是斥力。由于这个斥力的存在,奥陌陌运行轨道会加速偏离标准的双曲线轨道;速度上,奥陌陌刚进入太阳系后会逐渐加速,奥陌陌过近日点(奥陌陌运行方向与引力线夹角为90˚)后,奥陌陌速度还在迅速增加,奥陌陌运行方向和引力线夹角93˚时,加速达到峰值,此后加速迅速下降,但是速度任然在缓慢增加。通过对奥陌陌运行轨道的模拟,可以看出:奥陌陌的轨道偏离和异常加速都是奥陌陌运行方向和太阳引力线夹角超过90˚以后,受到太阳斥力的必然结果。