1. 引言
质量、动能和作用力关于时空的二阶偏微分方程式(1),简称MEF方程 [1]
(1)
MEF方程揭示了作用力和质量的本质以及质量和能量相互转化的时空原理,反映了质量、动能和作用力之间的内在关系,以及它们在时空中的瞬间效应。当不考虑相对论效应时,MEF方程主要揭示了物体的粒子特性,没有涉及到物体的波动特性。
本文通过考虑相对论效应,将相对论效应引入MEF方程,从速度为0到光速c,从光子到实物粒子,对MEF方程进行全方位探讨,建立了光子和实物粒子的相对论MEF方程,揭示了光子以及实物粒子的波动特性和粒子特性的本质和内在联系。实物粒子的波粒二象性通过相对论MEF方程分解出的粒子特性MEF方程和波动特性MEF方程体现出来,并随着速度的增加不断向波动特性MEF方程转化,如果可以达到光速,则将完全转化为光子相对论MEF方程,实现实物粒子向光子的转化。
本文通过对力的本质进行分析,推断出实物粒子在被斥力加速时,如果施力粒子质量小于或等于实物粒子质量,则实物粒子无法被加速到光速,反之,实物粒子将有可能被加速到光速。当实物粒子被引力加速时,将也有可能被加速到光速。本文还揭示了实物粒子质量由静止质量到运动质量再到光子运动质量的转化过程以及三种质量之间的关系。通过对粒子波动系数的分析,推导出了在接近和达到光速时,实物粒子运动质量新的计算公式。
2. 相对论与非相对论MEF方程
根据相对论,物体静止状态下表现出的质量为静止质量,物体运动时表现出的质量为运动质量,运动质量随物体速度大小的变化而变化 [2] 。设静止质量为
,运动质量为m,二者的关系如下
(v为粒子速度,c为光速)(2)
当
时,不考虑相对论效应,式(1)中物体的运动质量m可认为是不变量,和物体静止质量m0相等,这时MEF方程可表述为
(m0为静止质量) (3)
由于MEF方程式(1)反映的是各物理量的瞬间对应关系 [1] ,如果考虑相对论效应,式(1)中的物体质量m应为运动质量,它随物体速度大小的变化而变化。
为区别起见,本文称质量为运动质量的式(1)为相对论MEF方程,质量为静止质量的式(3)为非相对论MEF方程。论文《质量、动能和作用力关于时空的二阶偏微分方程的研究》 [1] 主要是讨论非相对论MEF方程,研究的是物体的粒子特性。
3. 光子的相对论MEF方程
根据相对论和量子理论,光子作为一类特殊的粒子,没有静止质量,但有运动质量 [3] ,光子具有的能量E [4] 与其频率γ及运动质量m的关系为 [2]
(h为普朗克常量,γ为光子频率) (4)
即
(5)
从爱因斯坦质能方程与动能方程 [2] 知道,对于光子来说,
,和式(5)一起代入相对论MEF方程式(1),可得
(6)
式(6)就是光子的相对论MEF方程。
3.1. 光子的波动特性
通过解光子的相对论MEF方程式(6),我们可以得到该方程的一个复数解
(其中
) (7)
式(7)是标准波函数的复数形式 [4] ,波速为c。从式(7)可以看出光子的相对论MEF方程式(6)反映了光子运动具有标准的波动特性,光的干扰、衍射以及光的传播等都是光子波动特性的具体表现。
3.2. 光子的粒子特性
在论文《质量、动能和作用力关于时空的二阶偏微分方程的研究》 [1] 中,我们知道
是作用力的一种表达形式,从光子的相对论MEF方程式(6)我们可以得到
(8)
式(8)表明,光子作为一类特殊的粒子,可以和其他粒子发生力的作用,光子所受作用力的大小和光
子本身的能量及能量对时间的二次偏导成正比,光子所受作用力的方向为光子位移改变的方向
。当光子能量发生变化即光的频率发生变化时,光子一定和其它粒子发生了力的作用,体现出光子的粒子特性,比如光压效应、光热效应、光电效应、光的反射、折射以及光子对撞反应等。如果通过高能量碰撞导致光子光速终止,光子相对论MEF方程将转化为实物粒子相对论方程(后文讨论),光子将转化为实物粒子。论文《质量、动能和作用力关于时空的二阶偏微分方程的研究》 [1] 中对高能光子碰撞产生电子对的研究就证明了这一点。
4. 实物粒子的相对论MEF方程
根据相对论,对于运动的实物粒子来说,其运动质量m和静止质量m0的关系由式(2)确定 [2] 。设
,由式(2)可得
(9)
根据爱因斯坦质能方程及动能方程 [2]
(10)
将式(9)代入式(10)
(11)
所以
(12)
将式(12)代入相对论MEF方程式(1)可得
(其中
) (13)
式(13)就是实物粒子的相对论MEF方程。
4.1. 实物粒子的粒子特性
当
时,即
时
(14)
实物粒子的相对论MEF方程式(13)变为
(15)
由
及式(9)、式(11)可得
(16)
将式(16)代入式(15)可得式(3),即
(3)
由于式(3)是完全体现粒子特性的非相对论MEF方程,所以式(15)体现的也是粒子特性,我们称式(15)为粒子特性MEF方程。因此,在
时,实物粒子的相对论MEF方程式(13)转化为粒子特性MEF方程式(15)。
4.2. 实物粒子的波动特性
当v接近c,即
时
(17)
实物粒子的相对论MEF方程式(13)变为
(18)
式(18)和式(6)光子相对论MEF方程形式一样,只是将光子的光速c替换为粒子的速度v,通过解方程式(18),我们也可以得到该方程的一个复数解
(其中
) (19)
在量子力学中描述自由粒子运动的物质波函数的复数形式通常表述为 [4]
(20)
式(19)和式(20)具有相同的形式,所以方程(18)的解式(19)也是一个标准的波函数,波速为v,反映出当速度v接近光速c时,实物粒子将以一种接近波的形式存在,这种波就是德布罗意物质波。量子力学认为物质波不是实际物理量的波动,只是刻画粒子空间分布的概率波,它“引导”粒子运动,决定粒子在空间各点出现的概率 [5] 。从本质上来说,式(7)体现的有关光子的波也是一种概率波,决定了光子在空间各点出现的概率。
以上分析说明,当实物粒子速度v接近光速c时,实物粒子相对论MEF方程式(13)将转化为和光子相对论MEF方程相同的形式即式(18),体现的是实物粒子的波动特性,我们称式(18)为波动特性MEF方程。
如果实物粒子速度v能达到光速c时,这时β = 1,实物粒子相对论MEF方程式(13)将完全转化为光子相对论MEF方程式(6),实物粒子转化为光子。同样,如3.2节所述,当通过高能碰撞导致光子光速终止时,光子相对论MEF方程式(6)将转化为实物粒子波动特性MEF方程式(18),进而转化为实物粒子相对论方程式(13),光子转化为实物粒子。
4.3. 实物粒子的波粒二象性
实际上只要速度介于0和光速c之间,实物粒子就会表现出波粒二象性,只是速度越小,波动特性表现得越弱,粒子特性表现得越强。反之,速度越大,波动特性表现得越强,粒子特性表现得越弱。
式(13)是实物粒子的相对论MEF方程,可表示为两个方程之和,这两个方程分别为
(21)
(22)
即式(13) = 式(21) + 式(22)。
化简后,式(21)和式(22)分别成为粒子特性MEF方程式(15)和波动特性MEF方程式(18),即
(15)
(18)
由前文我们知道,粒子特性MEF方程式(15)体现的是实物粒子的粒子特性,而波动特性MEF方程式(18)是德布罗意物质波函数的波动方程,体现的是实物粒子的波动特性。所以实物粒子的相对论MEF方程式(13)既能体现实物粒子的粒子特性,也能体现实物粒子的波动特性。
式(21)和式(22)的项
的系数分别为
和
,体现了实物粒子的粒子特性和波动特性在粒子整个运动特性里的占比,我们称
和
分别为实物粒子的粒子特性系数和波动特性系数。
表1列出了不同β (= v/c)值对应的实物粒子的粒子特性系数
和波动特性系数
的值。

Table 1. The values of particle characteristic coefficient 1 − β 2 and the wave characteristic coefficient ( 1 − 1 − β 2 ) of physical particles corresponding to different β (= v/c) values
表1. 不同β (= v/c)值对应的实物粒子的粒子特性系数
和波动特性系数
的值
图1是随着β的变化实物粒子的粒子特性系数
和波动特性系数
值的变化曲线图,也反映了随着速度的变化实物粒子的粒子特性和波动特性在整个粒子运动特性里的占比变化情况。
从图1可以看出,当实物粒子速度v为0即β等于0时,粒子特性系数
为100%,波动特性系数
为0%,实物粒子的相对论MEF方程完全表现为粒子特性MEF方程,质量表现为静止质量。
当实物粒子速度0 < v < c时,系数
和
都不为0,构成实物粒子相对论MEF方程的粒子特性MEF方程和波动特性MEF方程的占比也都不为0,所以实物粒子表现为波粒二象性,质量表现为随速度大小变化的运动质量。v越大,波动特性系数
越大,波动特性MEF方程占比也越大,粒子波动特性表现得也就越强。
如果实物粒子速度v能达到光速c即β等于1时,粒子特性系数
为0%,波动特性系数
为100%,实物粒子相对论MEF方程完全表现为波动特性MEF方程,成为光子相对论MEF方程,实物粒子湮灭为光子,质量表现为相应光子的运动质量。
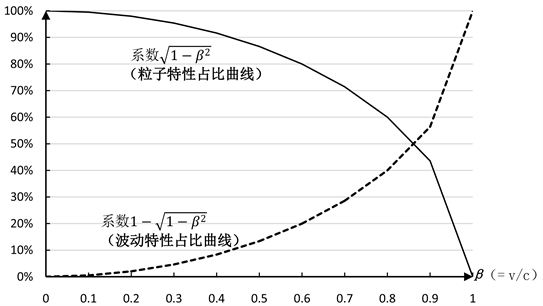
Figure 1. The proportions of particle characteristic and wave characteristic of physical particles vary with β
图1. 实物粒子的粒子特性和波动特性占比随β变化图
5. 实物粒子与光速
实物粒子到底能否被加速到光速?根据爱因斯坦的相对论质量公式(2),即
(2)
达到光速c的实物粒子的运动质量将变为无穷大,这当然是不可能的 [2] 。
通过4.3节的分析,理论上实物粒子运行到光速时,将完全转化为光子,实物粒子运动质量将完全转化为光子运动质量,应该说正反粒子互相湮灭为等能量的光子就证明了这种转化过程。
对于实物粒子来说,可以利用系数
定义另外一种形式的质量mp,即
(23)
也即
(24)
在式(24)中,当β = 1即v = c时,m = mp,所以mp的物理意义就是实物粒子速度达到光速后的运动质量,也就是实物粒子完全转化为光子后光子的运动质量。如果利用能量守恒定律能求出实物粒子完全转化为光子后光子的运动质量mp,和式(2)类似,式(24)也可以成为计算实物粒子在速度为v时的运动质量,特别是在实物粒子被加速到光速时,式(24)能正确反映实物粒子运动质量的变化和数值。式(24)的不足之处在于,当v = 0时,式(24)求出的运动质量为无穷大。所以计算实物粒子的运动质量时,式(2)更适合低速情况,而式(24)更适合高速情况,这需要经过具体实验进行进一步论证。
通过上文分析,当实物粒子达到光速时,如果利用式(24)计算实物粒子运动质量,不会出现式(2)计算出的无穷大的结果 [2] ,而是能很合理地得到相应光子运动质量的结果,所以理论上来说,实物粒子完全可以被加速到光速。
在实践中,如果要对一个实物粒子进行加速,必需对它施以作用力,从论文《质量、动能和作用力关于时空的二阶偏微分方程的研究》 [1] 我们知道,所有作用力的产生都是粒子碰撞的结果,粒子碰撞主要分两种:一种产生斥力,一种产生引力。
如果通过斥力也就是推力对实物粒子进行加速,施力粒子本身的速度只有大于被加速粒子,才能起到加速作用。当施力粒子质量小于或等于被加速粒子时,根据碰撞原理 [3] ,随着实物粒子的速度提高,和施力粒子的速度会越来越接近,目前我们认为光速是所有物体速度的极限 [2] ,所以我们能提供给施力粒子最大的速度只能是光速,这种施力粒子就是光子。随着实物粒子的速度提高,将会越来越接近光子的速度即光速,由于光速是速度的极限,被加速粒子速度v的变化空间会越来越小,所以实物粒子动能EK的变化空间也会越来越小,根据MEF方程 [1] ,
,加速作用力也会越来越小,被加速粒子接近光速时,加速作用力将接近于0,这样被加速实物粒子只能是不断接近光速而很难真正达到光速。当施力粒子质量大于被加速粒子时,如果发生弹性碰撞,根据碰撞原理 [3] ,被加速粒子的速度有可能达到施力粒子的两倍,这时被加速粒子的速度就有可能达到光速,湮灭为光子,这也是在某些粒子碰撞中能产生光子的原因 [5] 。
如果对实物粒子的加速作用力来源于产生引力的碰撞,根据论文《质量、动能和作用力关于时空的二阶偏微分方程的研究》 [1] ,随着被加速粒子速度的增加,加速的作用力不降反升,那么被加速粒子的加速度将不断增加,速度也将不断增加 [1] ,如果空间足够,被加速粒子就很容易达到光速,这种情况就发生在利用引力加速的系统中,本质上来说是利用保守力消耗系统内部势能来增加系统动能的方式对粒子进行加速。最典型的例子就是正反粒子对之间的湮灭反应,正反粒子对之间的与距离的平方成反比的引力将正反粒子对轻易地加速到光速,正反粒子对将完全以光波的形式存在,也就是转化成了光子,从公式(24)也可以看出,粒子运动质量完全转化为相应光子的运动质量,完成湮灭反应。当然,不是所有的引力加速都能将实物粒子加速到光速而湮灭。如果在加速过程中,加速的空间不够,比如物体落向地面,加速就会被终止,或者实物粒子将加速引力转变为向心力而围绕施力中心做圆周运动,被加速粒子的速度将不会继续增加,它将处于稳定的圆周运动状态而不被湮灭,原子核通过引力捕获电子的过程就是这种情况的典型例子。
其实,在很多物理、化学和核反应中都存在将实物粒子加速到光速并湮灭的情况,其中最显著的特征就是反应过程中产生光,比如燃烧反应、电极之间的放电、核聚变等,就产生强烈的可见光,这是由实物粒子被加速到光速后湮灭变成光子的结果。当然,除了可见光,还有其它电磁波,也是由湮灭反应产生的光子组成,所以凡是产生电磁波的反应都意味着存在实物粒子被加速到光速而被湮灭为光子的现象。
由于速度是一种相对物理量,其值只是针对处于某个参照系的特定观察者才有意义,所以这里讨论的静止质量、运动质量、粒子特性、波动特性等也都是具有相对性质的物理量,它们的值也只是针对某个参照系的特定观察者才有效。不同参照系观察到的实物粒子和光子的能量和运动质量都会有所不同,而光子的能量和频率有关,所以这也是不同参照系观察同一束光会具有不同频率并产生红移、蓝移的原因。
需要说明的是,实物粒子如果在某一个参照系里不能被加速到光速时,那么在任何其他参照系都不可能被加速到光速。实物粒子在某一个参照系被加速到光速并转化为光子,在任何其他参照系也将会被加速到光速并转化为光子,只是达到光速并湮灭为光子的时间会不一样,这些现象是相对论的有关相对性原理造成的 [2] ,这里不多述。
6. 结论
论文《质量、动能和作用力关于时空的二阶偏微分方程的研究》 [1] 从经典力学推导出了质量、动能和作用力关于时空的二阶偏微分方程
,由于MEF方程反映的是各物理量的瞬间对应关系,当考虑相对论效应时,式中m应为相对论描述的运动质量,该式即成为相对论MEF方程。粒子的波粒二象性的本质就体现在相对论MEF方程。
光子作为一类特殊的粒子,没有静止质量,但有运动质量,其相对论MEF方程为
,从该方程可以推断出,具有波动特性的光子,以光速前进。当与其它粒子碰撞时,随着自身能量的改变,将和其它粒子发生力的作用,呈现出一定的粒子特性。如果某些高能碰撞能使光子的光速终止,光子相对论MEF方程将转化为实物粒子相对论MEF方程,光子将转化为实物粒子。
实物粒子的相对论MEF方程为
,其中
。实物粒子的相对论MEF方程可分解为粒子特性MEF方程
和波动特性MEF方程
,它们在相对论方程里的占比系数
和
随速度v的变化而变化,实物粒子行为呈现波粒二象性。随着速度的增加,波动特性MEF方程占比相应增加,实物粒子的波动特性变得越来越强。如果实物粒子能达到光速,粒子的相对论MEF方程将完全转化为光子相对论MEF方程,粒子转化为光子。
实物粒子在接近和达到光速时其运动质量应通过含有相应光子运动质量
的式(24)而不是含有粒子静止质量
的式(2)来计算。
通过加速,实物粒子的速度有可能达到光速而被湮灭为光子。产生光子(电磁波)的物理、化学或核反应都存在实物粒子被加速到光速而湮灭为光子的现象。
参考文献