基于小波阈值去噪和函数主成分分析的交通流预测

Traffic Flow Prediction Based on Wavelet Threshold Denoising and Functional Principal Components Analysis

摘要: 准确的交通流预测不仅有助于改善交通状况，而且有利于推动智能交通系统的发展。大多数当前的预测方法没有充分利用时间序列的潜在函数特性来进行预测。针对这个问题，本文提出了一个基于小波阈值去躁和函数主成分分析的交通流预测模型(Wavelet Threshold De-noising-Functional Principal Components Analysis, WTD-FPCA)。使用中国贵阳市真实的交通数据集对所提模型进行验证，并使用均方根误差(Root Mean Square Error, RMSE)，平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)和均方误差(Mean Square Error, MSE)来评价WTD-FPCA模型的预测性能。在预测性能比较中，我们考虑了季节差分自回归移动平均(Seasonal Autoregressive Integrated Moving Average, SARIMA)、长短期记忆(Long Short-Term Memory, LSTM)网络、循环神经网络(Recurrent Neural Network, RNN)和门控循环单元(Gate Recurrent Unit, GRU)。预测结果表明，WTD-FPCA模型的预测性能最优。

Abstract: Accurate traffic flow forecasting not only helps to improve traffic conditions, but also facilitates the development of intelligent transportation systems. Most current forecasting methods do not make full use of the potential function property of time series for prediction. To address this problem, a traffic flow prediction model based on Wavelet Threshold Denoising and Functional Principal Components Analysis (WTD-FPCA) is proposed in this paper. The proposed model is validated using a real traffic dataset in Guiyang, China, and the Root Mean Square Error (RMSE), Mean Absolute Percentage Error (MAPE) and Mean Square Error (MSE) are used to evaluate the prediction performance of the WTD-FPCA model. For the prediction performance comparison, we considered Seasonal Autoregressive Integrated Moving Average (SARIMA), Long Short-Term Memory (LSTM) network, Recurrent Neural Network (RNN) and Gate Recurrent Unit (GRU). The prediction results show that the WTD-FPCA model has the best prediction performance.

1. 引言

在智能交通系统的发展中，交通流量预测是一个至关重要的问题，因为涉及到交通拥堵问题的有效解决 [1] 。准确的交通流预测可以为交通管理部门制定相应的交通管理控制方案，并为出行者提供精准可靠的出行路线，从而提高出行的效率，而这些只能通过发展预测模型来实现 [2] 。

由于交通流的动态特点，以及不稳定的交通状态和不可预测的环境因素，使得交通流预测的精度面临一定的挑战。现在有大量文献完全集中在预测模型上。文献 [3] 对现有的交通流量预测文献进行了分类和分析，并且介绍了交通预测研究中的相对薄弱领域及对智能交通系统的贡献。经过多年的发展，交通流的预测研究取得了很大的进展。从发展的进程来看，交通流预测模型和方法大概可以分为两类：经典的方法和基于深度学习的方法。经典的方法包括统计方法和传统的机器学习方法。统计方法是通过构建一个数据驱动的统计模型进行预测。最具有代表性的有差分自回归移动平均(Autoregressive Integrated Moving Average, ARIMA) [4] 和向量自回归(Vector Autoregression, VAR) [5] 。然而，这些方法只适用于相对较小的数据集，随着数据集增大，其预测精度不高。随着机器学习方法的迅速崛起，支持向量回归(Support Vector Regression, SVR) [6] 和随机森林回归(Random Forest Regression, RFR) [7] 等被提出用于交通流预测问题。这些方法具有处理高维数据和捕捉复杂非线性关系的能力。虽然这些方法在交通流预测中被证明是有效和可行的，但它们通常需要更高的计算负荷和存储压力。当有大量训练样本的情况下，这是不合适的。随着深度学习方法的发展，人工智能才逐渐在交通流预测中发挥出它的实力 [8] 。这项技术研究如何学习一个分层模型，并将原始输入直接映射到输出 [9] 。最具代表性的深度学习方法有循环神经网络(RNN) [10] ，LSTM [11] 和GRU [12] 。然而，与经典方法相比，它也存在一些缺点。深度神经网络比经典算法的计算成本更高且被认为是缺乏可解释性的“黑箱”。

函数型数据分析的统计工具在过去几十年得到广泛发展和应用。在Ramsay和Silverman [13] 以及Ferraty和Vieu [14] 的专著，Rice [15] ，Zhao等人 [16] 以及Müller [17] 的综述文章中提供了关于函数型数据分析的系统概述。在FDA中，数据被看作是在一个连续的函数空间中变化的函数，而不再是传统的多维数据点。这些函数可以代表曲线、曲面、图像、时间序列等。2012，Chiou [18] 首次提出将FDA用于交通流数据分析和预测，通过将交通流轨迹看作时间的函数，提出将函数预测与概率函数分类相结合的函数混合预测方法。2014，Guardiola [19] 基于FDA提出一种新方法来分析每日交通流量曲线，并使用FPCA来概括日常交通流量的变化。但在文献 [19] 中作者没有使用函数主成分来产生准确的交通流量预测。2017，Crawford [20] 采用不同的方法来分析函数交通流，并且使用函数线性模型来分析交通流。该模型用于描述交通流曲线的可预测波动，并且分析交通管理政策的潜在影响。但在 [20] 中需要专家知识来选择线性模型的变量。在 [18] [19] [20] 工作的基础上，Isaac等人 [21] 提出使用函数主成分分析来构建高质量的在线交通流预测，与文献 [18] [20] 不同的是，该方法不需要对历史交通数据进行聚类，并将常用的时间序列预测方法应用于数据的FPCA表示，且在模型选择过程中需要人为干预的相对较少。同时由于交通流数据具有随机性和非线性特征，使数据存在异常值的可能。因此需要对交通流数据进行异常值处理，从而减少对后续交通流数据分析的影响。

针对以上问题和在前人工作的基础上，本研究提出一个基于小波阈值去躁和函数型主成分分析(WTD-FPCA)的交通流预测模型，该方法使用小波阈值去躁对交通流数据中异常值数据进行降躁处理，然后使用函数主成分来创建一个可靠的交通流预测。

2. 方法原理

2.1. 小波阈值去噪(WTD)

小波阈值去噪方法由Donoho [22] 提出的，其实质是抑制信号中的无用部分、增强有用部分的过程。小波阈值去噪的过程如图1所示。

Figure 1. Wavelet threshold denoising process

图1. 小波阈值去噪过程

小波分解如公式(1)所示，其中t是时间点， $f\left(t\right)$ 是原始数据， $\psi$ 是小波基函数，a是比例，b是平移尺度。

$WT\left(a,b\right)=\frac{1}{\sqrt{a}}{\displaystyle {\int }_{-\infty }^{\infty }f\left(t\right)\ast \Psi \left(\frac{t-b}{a}\right)\text{d}t}$ (1)

小波分析对原始交通流数据的高频和低频向量进行分解，并对高频向量进行阈值处理，最后重构为降噪数据。详细的设计的过程如下。

1) 小波基函数的选择

对于不同类型的数据，需要选择不同的小波基函数，其定义如公式(2)所示。在公式(2)中，a，b， $\psi$ 和t和上面的定义相同。本研究选择dmey基函数。

${\Psi }_{a,b}=\frac{1}{\sqrt{\left|a\right|}}\Psi \left(\frac{t-b}{a}\right)$ (2)

2) 分解水平

数据中可能存在的噪声需要在不同尺度下进行分析和去除。不同的分解水平对应不同的分析尺度，每个分解层数采用不同的尺度对原始信号进行测量，随着层数的增加尺度逐渐细化。本研究分解水平设置为3。

3) 阈值方法

在小波阈值去噪的过程中，小波阈值选取准则的确定是一个关键的步骤，小波阈值的选取方法一般包括无偏风险估计阈值、固定阈值、启发式阈值、以及极大极小阈值等四种准则。本研究采用了无偏风险估计阈值(Rigrsure)原则：

将交通流数据 $S_i$ 的每个元素取绝对值后得到新的序列 $f\left(k\right)$ ，按从小到大的顺序进行排序，然后取平方：

$f\left(k\right)={\left(sort\left(\left|S_i\right|\right)\right)}^2,i=0,1,2,\cdots ,m-1$ (3)

若阈值为 $f\left(k\right)$ 的第k个元素的平方根，则

${\lambda }_k=\sqrt{f\left(k\right)}$ (4)

那么阈值产生的风险为：

$Risk\left(k\right)=m-2k+\frac{{\displaystyle {\sum }_{i=1}^{k}f\left(i\right)+\left(m-k\right)f\left(m-k\right)}}{m}$ (5)

风险曲线 $Risk\left(k\right)$ 中的 $k_{\min }$ 表示最小风险点对应的k值。Rigrsure原则的阈值常数定义如下：

$\lambda =\sqrt{f\left(k_{\min }\right)}$ (6)

选择阈值函数来过滤含噪声的小波系数并去除高斯噪声。最常用的阈值函数是软阈值函数和硬阈值函数。通过软阈值处理会使数据的曲线更加平滑，在保留有效信息的同时，尽可能的去除噪声。硬阈值的处理会保留尖峰特征，虽然去噪较为彻底，但很容易去除被误认为是噪声的有用信息。因此，本研究采用软阈值函数，其定义如下：

${\stackrel{⌢}{W}}_{j,k}=\{\begin{array}{l}\mathrm{sgn}\left(W_{j,k}\right)\left(\left|W_{j,k}\right|-T\right),\left|W_{j,k}\right|\ge T\\ 0,\left|W_{j,k}\right|<T\end{array}$ (7)

$W_{j,k}$ 和 ${\stackrel{⌢}{W}}_{j,k}$ 表示含噪输入和输出数据的小波系数，T为阈值， $\mathrm{sgn}(\cdot )$ 为阶跃函数。

2.2. 函数主成分分析(FPCA)

本文使用Wagner-Muns et al. [21] 提出的函数主成分分析来进行交通流预测。与 [21] 不同的是，我们使用傅里叶基函数去更好地拟合离散时间序列。FPCA步骤如下：

Step 1：使用傅里叶基函数拟合去噪后的交通流时间序列，以产生函数主成分和得分。

Step 2：使用SARIMA模型去拟合每一个函数主成分得分，以产生下一天的主成分得分预测。

Step 3：随着时间的推移将会进入到预测日，使用预测日的部分观测值来估计当天的主成分得分。

Step 4：将预测的主成分得分与估计的主成分得分相结合，以产生一天中剩余部分的交通流预测。

Step 5：最后将预测的值与观测的值进行比较，确定预测区间。

3. 结果与讨论

3.1. 数据来源

用于验证本文方法的数据来源于贵州省贵阳市长岭南路与阳关大道交叉口的检测点采集的交通流数据。该数据集从2021年3月1日至3月31日，每5分钟采集一次，每天包含288个数据，共收集31天。将前30天的数据作为训练数据，第31天的早上6点至晚上24点的数据作为测试集，用于测试最终模型的预测结果。由于检测点检测器存在问题以及其他随机因素的可能，导致数据集存在为零的数据。为了保证数据的周季节性，将数据中为零的数据替换为对应的前一周的数据。在31天的时间序列数据中，有5天被替换了。

3.2. 实验环境和预测性能评价

实验环境是一台服务器(CPU: Intel(R) Core(TM) i5-10500, GPU: Inter(R) UHD Graphics 630 16 GB)。

预测性能的评价用到3个指标，分别为均方根误差(RMSE)、平均绝对误差(MAE)和绝对百分比误差(MAPE)，分别定义为：

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(Y_{real}\left(t\right)-Y_{pred}\left(t\right)\right)}^2}}$ (8)

$\text{MAE}=\frac{1}{n}{\displaystyle \underset{t=1}{\overset{n}{\sum }}\left|\left(Y_{real}\left(t\right)-Y_{pred}\left(t\right)\right)\right|}$ (9)

$\text{MAPE}=\frac{100\%}{n}{\displaystyle \underset{t=1}{\overset{n}{\sum }}\left|\frac{Y_{pred}\left(t\right)-Y_{real}\left(t\right)}{Y_{real}\left(t\right)}\right|}$ (10)

其中， $Y_{real}\left(t\right)$ 表示在t时刻的交通流的实际值； $Y_{pred}\left(t\right)$ 表示预测值，n表示样本个数。

3.3. 小波阈值去噪交通流数据

本研究采用了WTD方法对原始交通流数据进行降噪处理。其中小波基函数选择dmey [23] ，分解水平设置为3，采用软阈值函数。WTD的降噪结果如图2所示，降噪后的数据曲线更加平滑，在保留有效信息的同时，尽可能的去除噪声。

Figure 2. Denoised result

图2. 降噪结果

3.4. 使用基函数拟合去噪的交通流数据

首先使用傅里叶基函数去拟合去噪后的离散时间序列。平滑惩罚参数 $\lambda$ 的确定通过对GCV在多个不同的平滑惩罚值下分析确定的。这里选择 $\lambda ={10}^2$ 最小化GCV准则。为了进一步验证函数拟合的质量，对残差进行了检验。图3提供了一个说明，函数交通流时间序列很好地逼近了离散时间序列。

Figure 3. Histogram of fitting residuals

图3. 拟合残差直方图

3.5. 产生函数主成分

虽然已经构建了离散时间序列的光滑函数表示，但这种处理会使得傅里叶基函数之间存在较强的相关性。通过函数主成分分析它们之间的相关性，以降低数据的维度，表示其可预测的变化模式。

通过方差贡献率确定前四个主成分表征了函数时间序列数据中95%的变化。在生成交通流预测时，利用FPCA减少数据的变化，会使模型对交通中的瞬时变化(如车祸)更加稳健。FPCA保留了时间序列中的主要变化模式。在很多情况下，第一主成分函数直接对应于数据中明显可观测的现象 [24] 。

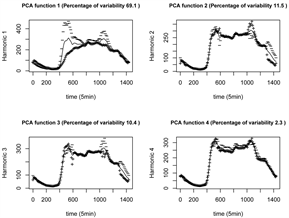
Figure 4. Demonstration of how FPCA harmonics modify the mean function

图4. 展示FPCA谐波如何修改平均函数

如图4所示，可以看出它们的高峰期是一致的。每一天在原始离散数据集需要用288个值去描述，而每一个FPCA表示一天的交通流只需要4个值。这样能降低数据集的维度和相关性，减少预测的复杂性。

3.6. 使用SARIMA模型拟合函数主成分得分

只要确定使用FPCA表示数据，下一步就是确定每天FPCA得分的模型。第一步对FPCA得分进行分析，判断是否需要将季节性纳入模型。图5是30天的前三个FPCA得分的散点图，其中每一个点的颜色代表一周中的一天。散点图表明具有周季节性。同时图6中偏自相关图也证实了具有周季节性。所以函数主成分得分的SARIMA模型包含周季节性，即m = 7。

Figure 5. 3d scatter plot of FPCA scores colored by day of week. (Mon: Blue, Tues: Red, Wed: Green, Thurs: Orange, Fri: Black, Sat: Purple, Sun: Grey)

图5. FPCA得分的三维散点图，按星期的颜色划分。(星期一：蓝色，星期二：红色，星期三：绿色，星期四：橙色，星期五：黑色，星期六：紫色，星期日：灰色)

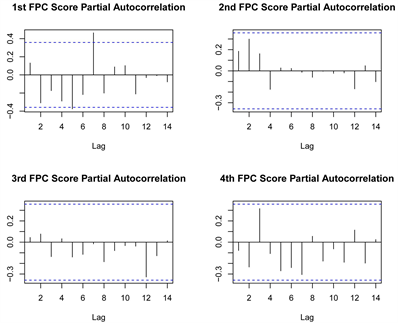
Figure 6. Partial autocorrelation of FPCA scores

图6. FPCA得分的偏自相关

接下来使用过去30天的函数主成分得分来确定模型的参数。模型参数使用R中auto.arima函数来自动确定，选择使AIC最小所对应的模型参数。最终前四个函数主成分得分所对应的模型为SARIMA (2, 0, 1) (1, 0, 1) 7，SARIMA (2, 0, 1) (0, 0, 0) 7，SARIMA (3, 0, 1) (1, 0, 0) 7，SARIMA (3, 0, 1) (0, 0, 0) 7。这些SARIMA模型将产生下一天的函数主成分得分预测。它们将与函数主成分得分估计相结合，以产生最终的函数主成分得分预测。

3.7. 产生预测和误差分析

尽管在3.6节中选择的SARIMA模型能够对下一天的交通行为产生准确预测，但它没有考虑到随着时间的推移进入预测日的新数据 [21] 。来自部分预测日的新信息将用来估计当天的FPCA得分。我们使用预测日这一天前6小时的交通流数据来估计当天的主成分得分。输出的主成分得分预测是由SARIMA模型预测产生的得分和由部分观测到的交通流信息估计得分的累积标准差加权的平均值。最后将加权平均的得分转换为函数表示，产生一天中剩余部分的交通流预测。

本文使用均方根误差(RMSE)、平均绝对误差(MAE)和平均绝对百分比误差(MAPE)来评价模型的预测性能。表1和图7表明，与传统的SARIMA模型相比，基于WTD-FPCA的模型产生的预测误差较小。图7说明WTD-FPCA模型除了具有较高的预测精度外，还对交通流中的瞬时事件具有较强的鲁棒性。此外，也说明了WTD-FPCA模型产生更一致的预测区间，因为它更好的描述了数据中的每周季节性现象。

Table 1. Performance comparison of different model

表1. 不同模型的性能比较

为了进一步评价所提出的WTD-FPCA模型的性能，与四种常见的模型SARIMA、LSTM、RNN和GRU分别进行对比分析。LSTM、RNN和GRU的超参数设置为：神经元个数：100，批处理大小为128，训练轮数：100，优化器：adam，激活函数：relu，Dropout：0.2，损失函数：MSELoss。图8展示了五种不同的预测模型的预测结果。从表1和图8可以看出SARIMA模型的预测性能最差，LSTM、RNN和GRU三种模型都比较准确地反映了真实的交通流量变化，相比之下WTD-FPCA更能准确的预测交通流。

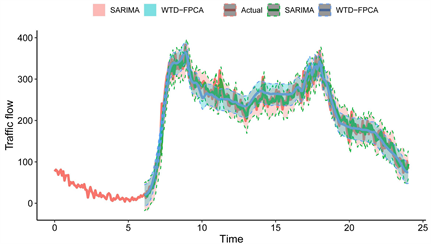
Figure 7. 90% prediction intervals for traditional SARIMA and WTD-FPCA

图7. 传统SARIMA和WTD-FPCA的90%的预测区间

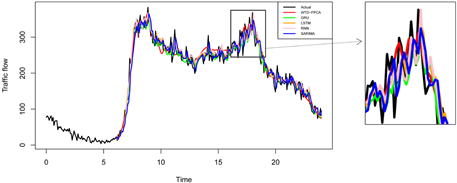
Figure 8. Prediction results of different models

图8. 不同模型的预测结果

4. 结论

本文分析了基于小波阈值去躁和函数主成分分析模型(WTD-FPCA)在交通流预测中的有效性。首先对数据进行预处理，然后使用小波阈值去躁，最后使用函数型主成分分析对未来交通流进行预测，并与四种常见的模型SARIMA、LSTM、RNN、GRU进行对比，使用MAE、MAPE和RMSE来评价模型的预测性能。从结果来看，WTD-FPCA模型的预测性能优于SARIMA、LSTM、RNN和GRU。WTD-FPCA模型除了具有较高的预测精度外，还对交通流中的瞬时事件具有较强的鲁棒性。函数型数据分析方法为观察和预测交通现象提供了一些新的视角，具有改进许多数据分析方法的潜力。

在未来的工作中，我们将尝试从两个方面对模型进行改进：

1) 本文使用预测模型FPCA，虽然为交通流预测提供了一些新思路，但与深度学习模型相比，预测性能还有较大的差距，因此考虑将分解算法和去噪方法与深度学习模型结合，以提高预测的精度。

2) 大规模路网预测也是值得研究的，可以考虑采用GNN来描述路网的几何特征，并将其与数据分解和去噪算法相结合，以达到提高模型预测性能和捕捉路网交通流时空特性的目的。