被动式三维重建在建立桥梁缆索数字模型中的应用

Application of Passive 3D Reconstruction in Establishing Digital Model of Bridge Cable

摘要: 在斜拉桥、拱式桥以及悬索桥等大跨径桥梁的建设中，缆索有着广泛的应用。缆索的有效承载能力会影响到桥梁的稳定和寿命，因此桥梁缆索的检测工作是一项十分重要的工作。建立缆索的数字模型可以方便后续的损伤检测工作，三维重建技术也因此在缆索检测问题上有着诸多应用。被动式三维重建是从一张或多张图片中恢复场景的几何结构，最终得到该场景的三维模型的方法。而通过被动式三维重建的方法，可以仅从桥梁缆索的影像数据来重建缆索的三维数字模型。本文使用缆索爬索检测机器人在移动过程中拍摄的影像数据进行实验，对获取的影像数据进行畸变矫正等数据处理；并根据桥梁缆索的几何结构分析得到相机位置信息，结合不同视点上的多幅图像恢复三维信息，最终得到三维模型。对最终重建模型选定4个点用作几何精度评定并与真值对比，选定点的相对误差分别达到了0.913%、1.196%、0.947%、0.568%，并得到平均绝对误差MAE为1.0053 mm。试验结果表明，本文提出方法可以在减少数据获取成本的同时得到纹理清晰、精度较高的模型。

Abstract: Cables are widely used in the construction of long-span bridges such as cable-stayed bridges, arch bridges and suspension bridges. The detection of the cables is a critical task, since the effective bearing area of the bridge cables will affect the stability and service life of the bridge. Establishing the digital model of the cable can facilitate the subsequent damage detection work. This led to many applications with 3D reconstruction technology in cable detection. Passive 3D reconstruction is a method to restore the geometric structure of a scene from one or more pictures, and finally obtain the 3D model of the scene. With the passive 3D reconstruction technology, the 3D digital model of the cable can be reconstructed only using the image data of bridge cables. In this work, the image data taken by the cable detection robot while moving is used for experiment, and data processing such as distortion correction is performed on the acquired image data. The information of camera position can be obtained based on the geometric structure of bridge cable. Combining this infor-mation with multiple images from different viewpoints, the three-dimensional information can be recovered for the final 3D model. For the final reconstructed model, 4 points were selected for geo-metric accuracy evaluation and compared with the ground truth. The relative errors of these chosen points reach 0.913%, 1.196%, 0.947% and 0.568% respectively, and the MAE is 1.0053 mm. The experimental results show that the method proposed can generate a model with clear texture and high accuracy, and also reduce the cost of data acquisition.

1. 引言

跨径桥梁，例如斜拉桥、拱式桥以及悬索桥等中，缆索都有着广泛的应用。在实际工程中，桥梁缆索承载着桥体三分之一的载荷，因此缆索的有效金属承载面积会影响到桥梁的稳定和寿命 [1] [2] 。在20至25年后，桥梁及缆索通常会进入病害高发期，出现开裂、锈蚀甚至引发桥梁断索、坍塌；因此，桥梁的损伤检测是预防桥梁安全问题的一个关键任务。近年来，出现了使用三维重建建立缆索的数字模型以方便进行检测的方法，为桥梁的损伤检测工作给出了新的方案 [3] 。

三维重建(3D reconstruction) [4] [5] 是指通过相机等传感器设备获取现实世界的影像等原始数据，并使用计算视觉的相关技术进行处理，最终得到场景或物体的三维模型的过程。获得的三维模型可以用于描述物体的外部特征，也可以应用在场景的模拟和显示等。三维重建技术对于混合现实(Mixed Reality, MR)、增强现实(Augmented Reality, AR)、机器人导航以及自动驾驶等研究都具有重要作用。

目前三维重建使用的主要方法可以大致分为主动式和被动式两类。主动式三维重建的方式采用传感器发射并接收预设信号的方式直接获取场景的三维信息，进而对场景进行三维重建。目前常用于主动式三维信息获取的传感器主要有结构光传感器、RGB双目相机、三维激光扫描仪以及飞行时间相机。a) 结构光三维重建技术，通过传感器发射提前设计好的具有特殊结构的图案信号(比如离散光斑、条纹光、编码结构光等)，并将这些图案投影到三维空间物体表面上，就可以在另外一台相机上观察在三维物理表面成像的畸变情况 [6] [7] [8] 。b) RGB双目相机由三角法原理进行三维信息的获取 [9] [10] 。其具体原理是由两个摄像机的图像平面和被测物体之间构成一个三角形；进而可以根据相机的基线距离、焦距、图中几何关系、坐标系转换即可求得目标体的三维信息。c) 三维激光扫描仪可以通过发射激光束的方式对三维场景进行扫描 [11] [12] 。d) 飞行时间相机(Time of Flight, TOF)技术则是通过计算红外载波的飞行时间来计算与物体之间的距离 [13] [14] 。

被动式三维重建是一种通过特定的算法从不含三维信息的RGB影像中获得场景的三维信息的技术，而不会主动获得三维信息(如深度d等)。该技术首先根据采集的影像，由标定算法计算每张影像的内参以及外参；根据计算得到的内外参可以得到每张影像的深度图；深度图的融合结果即为包含三维信息的密集点云 [15] 。而倾斜摄影测量技术作为一个新兴的技术方法可以为三维建模提供影像数据 [16] [17] [18] [19] [20] 。该技术可以减少盲区，有助于自动识别和重建。

被动式三维重建包含多种方式，如运动恢复结构(Structure from Motion, SfM) [21] [22] [23] 。其原理是从多个视点捕获的多张图像，并通过匹配算法获得图像中相同像素点的对应关系；再利用匹配约束关系及三角测量原理，获得空间点的三维坐标信息；进而重建出物体的三维模型。运动恢复结构法重建场景的三维结构不仅是三维重建的一种重要手段，也是一种结构测量的方法。这种方法能够广泛地应用在测绘、军事侦察等领域。目前SfM主要分为增量式SfM [22] [23] 和全局式SfM等类型。

常见的三维重建技术都需要用到相机的内外参数。当相机的内外参数没有校准时，则无法仅通过图像数据直接完成三角测量 [4] [24] [25] 。另一方面，即使有关相机参数的信息未知，人们直观地感觉到静态场景的每张图像都以一种或另一种方式约束了世界中物体的形状和相对位置，进一步了解和分析其工作原理以及解决3D重建问题的关键在于理解场景点在不同视图中的投影的位置点如何相互关联 [4] 。这种情况下就需要后续章节中介绍的投影三维重建技术，可以在未校准的情况下进行重建。

空中三角测量是被动三维重建技术的重要环节。空中三角测量的解算过程需要额外测量的控制点，也就需要依靠野外实测。因此人们也在不断探索减少地面控制点的方法，追求更高的自动化程度 [26] 。目前常用的辅助空中三角测量的方法是使用全球定位系统(Global Positioning System, GPS)和定位定向系统(Position and Orientation System, POS)辅助空中三角测量 [27] [28] [29] [30] 。POS数据主要包括GPS信号接收机和惯性测量单元(Inertia Measurement Unit, IMU)两个部分。IMU可直接获得测图所需的6个外方位元素，能够大幅减少乃至无需地面控制直接进行航空影像的空间地理定位。POS系统可以获取载体的位置和姿态信息，通过解算外方位元素参与区域网平差辅助空中三角测量。POS辅助解算方法已日渐成为主流。并且，当解算获得的外方位元素的精度足够高时，则可以直接应用外方位元素的前方交会法进行地面点定向，从而取消外业控制点和空中三角测量加密两个常规过程，实现由航空摄影直接到内业成图。

本文使用被动式三维重建的原理，并根据缆索影像数据的具体情况构造POS数据辅助完成空中三角测量，最终得到桥梁缆索的三维模型。该方法基于标定的相机在爬索机器人上的外方位元素以及内参数，在相机对缆索数据采用移动采集的情况下，仅通过RGB相机拍摄的影像数据重建出桥梁缆索的三维数字模型。

2. 三维重建关键技术

2.1. 被动三维重建

被动三维重建的目标是为了从一张或多张图片中恢复一个(静态)场景的几何结构 [4] ，可以将其描述为：给定一个点m，确定场景中的投影M。或用数学语言描述如下：在图像中，给定一个以像素坐标 $\left(x,y\right)$ 表示的像点m，确定场景点M的世界坐标 $\left(X,Y,Z\right)$ ，其中m是场景点在图像中的投影。

如果一个场景的两张图片都可获取，那么场景点M的位置就可由它的投影m₁和m₂通过三角测量恢复得到：点M就是m₁和m₂的投影射线的交点。但是当相机的内外参数没有校准时，无法单从图像数据就能精确的完成三角测量。另一方面，即使不知道有关相机参数的信息，人们直观地感觉到静态场景的每张图像都以某种方式约束了世界中物体的形状和相对位置。了解这种工作原理以及解决3D重建问题的关键在于理解场景点M在不同视图中的投影的位置点m₁和m₂如何相互关联。

从一个代数的观点来看，三角测量可以解释为求解关于场景点M的投影方程。因此，如果我们假设图片已经校正了径向畸变和其他的非线性效应，并且通用的线性针孔相机模型可用，那么我们可以得到如下的投影公式。

$\rho m=K{R}^{\text{T}}(M-C)$ (1)

其中， $M={\left(X,Y,Z\right)}^{\text{T}}$ 是场景点 $M$ 在世界坐标系下的坐标， $m={\left(x,y,1\right)}^{\text{T}}$ 是场景点 $M$ 在图片中的投影m的扩展坐标， $K$ 是相机的校准矩阵， $C$ 和 $R$ 分别表示世界坐标系下相机的位置和旋转矩阵，且 $\rho$ 是一个表示场景点 $M$ 相对于相机的投影深度的正实数。

由此得到，被动三维重建可以也被看作是求解下列方程：

${\rho }_1{m}_1=K_1{R}_1^{\text{T}}\left(M-C_1\right)$ (2)

${\rho }_2{m}_2=K_2{R}_2^{\text{T}}\left(M-C_2\right)$ (3)

这两个方程就是我们需要深入分析的部分。在传统的立体问题中，通常知道 $K_1,R_1,C_1,K_2,R_2$ 以及 $C_2$ 。又因为点 $M$ 的坐标以及缩放因子 ${\rho }_1$ 和 ${\rho }_2$ 可以通过计算得出，那么上述的公式就产生了一个由6线性方程和5个未知数组成的线性系统。然而，我们感兴趣的问题在于相机校准不完全的情形下，如何挖掘信息以完成三维重建。

2.2. 三维重建极线几何及影像匹配

对于上一节中问题，场景的第一张图像中的点 $m_1$ 是场景点 $M$ 的投影，该点 $M$ 可以在第一台相机中沿 $m_1$ 的投影射线的任何位置。因此，场景的第二张图像中的对应点 $m_2$ (即 $M$ 的投影)必须位于该投影射线在第二张图像中的投影 $l_2$ 上。假设两台相机的内参和外参均为已知，则点 $m_1$ 以及点 $m_2$ 的投影射线由方程(2)和(3)给出。

根据方程，我们可以进一步分析得到世界坐标系下像点 $m_1$ 以及像点 $m_2$ 的投影射线的参数方程，

$M=C_1+{\rho }_1{R}_1{K}_1^{-1}{m}_1,{\rho }_1\in ℝ$ (4)

$M=C_2+{\rho }_2{R}_2{K}_2^{-1}{m}_2,{\rho }_2\in ℝ$ (5)

将方程(4)代入第二个相机的投影方程(3)，得到，

${\rho }_2{m}_2={\rho }_1{K}_2{R}_2^{\text{T}}{R}_1{K}_1^{-1}{m}_1+K_2{R}_2^{\text{T}}\left(C_1-C_2\right)$ (6)

方程(6)右端第二项可以对应于第一台相机在第二张图像中位于位置 $C_1$ 时的投影 $e_2$ ：

${\rho }_{e_2}{e}_2=K_2{R}_2^{\text{T}}\left(C_1-C_2\right)$ (7)

$e_2$ 被称为第一台相机在第二张图像中的极点。另一方面，方程(6)右端的第一项表示第二张图像的投影射线的方向。可以看出 $R_1{K}^{-1}{m}_1$ 是 $m_1$ 的投影射线相对于世界坐标系的方向向量。在第二个相机以相机为中心的参考系中，该向量的坐标为 $R_2^{\text{T}}{R}_1{K}^{-1}{m}_1$ 。第二张图像中对应该观察方向的点由 $K_2{R}_2^{\text{T}}{R}_1{K}^{-1}{m}_1$ 给出。也即， $K_2{R}_2^{\text{T}}{R}_1{K}^{-1}{m}_1$ 是第二张图像中投影射线(4)的消失点的齐次坐标。

为简化记号，定义

$A=K_2{R}_2^{\text{T}}{R}_1{K}_1^{-1}$ (8)

其中 $A$ 为可逆3 × 3矩阵， $A$ 矩阵可以称作无限单应性矩阵。对于第一张图像上的像点 $m_1$ ，点 $m_1$ 在第二台相机中按照其在第一台相机中的投影射线投影得出的像点可以表示为 $A{m}_1$ 。那么由上述的公式(8)，可以将公式(6)化简为

${\rho }_2{m}_2={\rho }_{1}A{m}_1+{\rho }_{e_2}{e}_2$ (9)

根据这个公式可以理解相关的几何意义：对于一张图像中一个给定的像点 $m_1$ ，该场景的另一张图像中的对应点 $m_2$ 位于通过极点 $e_2$ 和第一台相机中 $m_1$ 视线的消失点 $A{m}_1$ 的线 $l_2$ 上。线 $l_2$ 被称为第二张图像对应于像点 $m_1$ 的极线，公式(9)被称为对应像点之间的极线关系。

上述的极线关系公式(9)通常表示为紧凑的代数表达式。为此，约定以下记号：对于一个三维向量 $a={\left(a_1,a_2,a_3\right)}^{\text{T}}\in {ℝ}^3$ ，令 ${\left[a\right]}_{\times }$ 表示如下的3 × 3的斜对称矩阵，

${\left[a\right]}_{\times }=\left(\begin{array}{ccc}0& -a_3& a_2\\ a_3& 0& -a_1\\ -a_2& a_1& 0\end{array}\right)$ (10)

由此可以表示 $a$ 的向量积，如， ${\left[a\right]}_{\times }v=a\times v,v\in {ℝ}^3$ 。且当 $a$ 为非零矩阵时即有 ${\left[a\right]}_{\times }$ 的秩为2。前文式(9)中的极线关系式表示，对于第一张图像中的点 $m_1$ ，该点在第二张图像中的对应点 $m_2$ 必须在穿过极点 $e_2$ 和消失点 $A{m}_1$ 的直线上。在代数上可表述为，代表对应像点齐次坐标的3维向量 $m_2$ ， $e_2$ ， $A{m}_1$ 应为线性相关。根据线性代数，上述条件等价于 $\left|\begin{array}{ccc}{m}_2& e_2& A{m}_1\end{array}\right|=0$ 。其中等式左边表示的是三个3维列向量组成的矩阵的行列式。再由向量积的定义可得 $\left|\begin{array}{ccc}{m}_2& e_2& A{m}_1\end{array}\right|=m_2^{\text{T}}\left(e_2\times A{m}_1\right)$ 。最终得到矩阵乘法形式 $\left|\begin{array}{ccc}{m}_2& e_2& A{m}_1\end{array}\right|=m_2^{\text{T}}{\left[e_2\right]}_{\times }A{m}_1$ 。

因此，极线关系式(9)可以等价表述为，

$m_2^{\text{T}}F{m}_1=0$ (11)

其中 $F={\left[e_2\right]}_{\times }A$ 为3 × 3矩阵，称为像对的基本矩阵，其中 $e_2$ 表示第二张图像的极点， $A$ 为(8)式中定义的可逆3 × 3矩阵。注意到， ${\left[a\right]}_{\times }$ 是秩为2的矩阵，因此基本矩阵 $F$ 的秩也为2。

基本矩阵 $F$ 对于极线关系的紧凑形式(10)具有以下优点：

a) 选取合适的非零标量因子可以仅从图像数据计算基本矩阵 $F$ 。

b) 给定 $F$ ，第二张图像中的极点 $e_2$ 是唯一的3维向量，第三个坐标等于1，满足 $F^{\text{T}}{e}_2=0$ 。

c) 类似地，第一张图像中第二个相机的极点 $e_1$ ，即第一张图像中第二个相机位置的投影 $e_1$ ，是唯一的3维向量，第三个坐标等于1，满足 $F{e}_1=0$ 。

d) 给定第一张图像中的点 $m_1$ ，第二张图像中 $m_1$ 对应的极线 $l_2$ 的齐次坐标为 $l_2\simeq F{m}_1$ 。

e) 类似地，给定第二张图像中的点 $m_2$ ，对应于 $m_2$ 的第一张图像中极线 $l_1$ 的齐次坐标为 $l_1\simeq F^{\text{T}}{m}_2$ 。

2.3. 投影三维重建

在得到了基本矩阵以及极线关系的表达式之后，我们就可以按照如下的算法完成三角测量。

通过求解该方程就可以得到场景 $\hat{M}$ 中的点，即成功将两张图像匹配到一起。

被动3D重建的目标是仅使用图像的3D相似变换来恢复场景结构的三维几何结构。但如果相机的校准矩阵未知，则场景结构仅能通过3D仿射变换来恢复。在此基础上，如果相机的配置信息也无法获取，则仅有投影三维重建方法可行。

2.4. 密集点云以及三维模型生成

影像匹配的准确性会直接影响到重建结果。常规航空摄影大多采用基于灰度或基于特征的单基元影像匹配方法。最小二乘匹配是一种基于灰度的影像匹配，其原理是通过迭代使灰度误差的平方和达到极小，从而确定出共轭实体的影像匹配方法。该方法能同时考虑到局部影像的灰度畸变和几何畸变。基于特征匹配的方法则需要首先在原始图像中提取特征，再建立两幅图像之间特征的匹配对应关系。

近年来一些研究中提出了多视影像密集匹配算法。大量的实验证明多视影像密集匹配能够获取高精度、高密度的点云，并能较好地解决了倾斜影像的匹配问题。目前最常用的密集匹配方法有带共线条件的多片最小二乘影像匹配方法、基于多基元多影像匹配方法、基于物方面元的多视立体匹配方法 [31] [32] 。

网格面模型是一种几何数据结构，通常由三角形组成描述物体表面。这种模型可由点云通过特定算法生成，比如区域增长法、八叉树算法和波前算法等 [33] [34] [35] 。而点云是同一空间参考系下用于表示目标空间分布和目标表面特性的海量点集合。内业软件基于几何校正及联合平差等处理流程，可计算出基于影像的超高密度点云。通过影像匹配过程可以得到高精度的密集点云；再由这些密集点云可以生成不规则三角网模型(Triangulated Irregular Network, TIN)；并通过倾斜影像自动纹理映射，给TIN模型表面赋予对应纹理；经过上述步骤，即可最终得到三维重建模型。

3. 实验及分析

3.1. 数据获取与POS构造

实验数据来自于珠江流域广东省某地的一座拉索桥。拉索桥有系到桥柱的缆索，并通过缆索支撑桥面的重量。该拉索桥的拉索为本实验三维重建的对象。

实验使用的桥梁拉索数据通过缆索检测机器人获得，如图1所示。机器人沿缆索移动的同时拍摄视频记录缆索数据；机器人在缆索的四个方向分别装有摄影机，总共可以获得四段影像数据。同时采用人工吊篮的形式测量得到真实的桥梁缆索直径。下一步的数据处理为将影像数据逐帧拆分为图片，分别得到按时间顺序排列的图片组以便后续实验。

本实验中数据处理的一个重要环节就是根据实验的影像数据构造POS数据。首先，由已知的缆索长度结合影像数据的时间得到相机的移动速度。根据相机安装于爬索机器人上的位置以及机器人的移动速度，每一张图片所处的位置可以大致地描述出来，即可由此构造每一张图片的POS数据。

将相机沿缆索移动的方向设定为y轴的方向， $x,y,z$ 分别表示相机位置的坐标，l为两张图片之间相机移动的距离。由此可以得到第k张图片的y坐标就可以表示为 $y+\left(k-1\right)l$ ，而 $pitch,yaw,roll$ 则分别表示相机的姿态角：俯仰，偏航，翻滚。

$\{\begin{array}{l}1:\left(x,y,z,pitch,yaw,roll\right)\\ 2:\left(x,y+l,z,pitch,yaw,roll\right)\\ ⋮\\ k:\left(x,y+\left(k-1\right)l,z,pitch,yaw,roll\right)\\ ⋮\\ n:\left(x,y+\left(n-1\right)l,z,pitch,yaw,roll\right)\end{array}$

Figure 1. Diagram of cable detection robot

图1. 缆索检测机器人图

根据机器人拍摄得到的四段影像，及根据上述方法得到的图片POS数据，即可分别得出四个方向的模型。而从四个方向分别建模的优点如下：

a) 相机的位置变化可由y坐标的变化来表示，而 $x,z$ 坐标以及旋转角度等其他参数不需要改变，POS数据的构造较为简单。

b) 另一方面，若所有方向的图片同时建模，则相机位置的表示就会变得比较复杂。

c) 此外，这样得到的模型在单个方向上缆索的弯曲程度不大，因此建出的模型可以将其先拟合到平面以方便配准而不至于损失过多纹理细节。

3.2. 空中三角测量及畸变矫正

上一节完成了数据获取及处理，并且已构造用于重建的POS数据。这一节将主要使用POS数据辅助完成空中三角测量。首先将四组图片按照拍摄方向的不同分为不同模块，为方便表示，将模块记为Block1，Block2，Block3，Block4。每个模块的图片组可按照图片名称将图片与位置和姿态信息(POS)匹配。然后对模块中的图片进行空中三角测量计算，即可得到图片匹配的结果。表1给出了关于Block1的空中三角测量结果，包含了模块属性的描述。其余模块的计算结果与之类似。

图2为相机镜头畸变的示意图，其中灰色网格表示零畸变的情况，而蓝色网格表示实验使用相机的畸变情况。可以看出实验使用图片存在部分桶形畸变，桶形畸变会在一定程度上影响位置精度。桶形畸变中，从图像的中心点到图像的边缘点图像的相对大小逐渐变小。图片发生桶形畸变时建模的质量也会受到影响，因此需要先对其进行畸变校正。目前最常使用的畸变校正模型是如下的偶数阶多项式模型 [36] 。

$\{\begin{array}{l}{x}_u=x_0+\left(x_d-x_0\right)\left(1+{\lambda }_1{r}_d^2+{\lambda }_2{r}_d^4+{\lambda }_3{r}_d^6+\cdots \right)\\ y_u=y_0+\left(y_d-y_0\right)\left(1+{\lambda }_1{r}_d^2+{\lambda }_2{r}_d^4+{\lambda }_3{r}_d^6+\cdots \right)\end{array}$ (12)

其中的 $\left(x_u,y_u\right)$ 以及 $\left(x_d,y_d\right)$ 分别为无畸变点和畸变点所对应的坐标，而 $r_d$ 则表示畸变点距畸变中心的欧氏距离。又因畸变中心为 $\left(x_0,y_0\right)$ ，有如下表达式。

$r_d^2={\left(x_d-x_0\right)}^2+{\left(y_d-x_0\right)}^2$ (13)

Table 1. Aero triangulation result of Block1

表1. Block1空中三角测量结果

Figure 2. Diagram of lens distortion

图2. 镜头畸变图

然而，在此模型中 $x_0,y_0,{\lambda }_1,{\lambda }_2,{\lambda }_3,\cdots$ 均为畸变参数，这也使得模型的计算较为困难。因此，除法模型提供了一种更好计算的畸变矫正方法，

$\{\begin{array}{l}{x}_u=x_0+\frac{x_d-x_0}{1+{\lambda }_1{r}_d^2+{\lambda }_2{r}_d^4+\cdots }\\ y_u=y_0+\frac{y_d-y_0}{1+{\lambda }_1{r}_d^2+{\lambda }_2{r}_d^4+\cdots }\end{array}$ (14)

如图2所示，本实验图片只存在轻微的桶形畸变，使用如下的单参数除法模型(即令 ${\lambda }_2={\lambda }_3=\cdots =0$ )可以很好的与之适配( $\lambda$ 为较小的负值) [37] [38] 。

$\{\begin{array}{c}\begin{array}{l}{x}_u=x_0+\frac{x_d-x_0}{1+\lambda r_d^2}\\ y_u=y_0+\frac{y_d-y_0}{1+\lambda r_d^2}\end{array}\end{array}$ (15)

使用单参数除法模型减少了畸变校正所需要的参数数量，因此只要选取合适参数进行计算就可以对相片进行校正。如图3所示为参数设置为 $\lambda =-0.02$ ，畸变中心设置为相片中心时，Block1中图片的校正结果。对于其他的模块同样选取合适参数进行畸变校正。

Figure 3. Diagram of distortion correction result

图3. 畸变校正结果

3.3. 三维模型生成及拼接

完成空中三角测量后仍需模型生成的相关步骤来完成最终三维重建。首先，通过区域增长法、八叉树算法及波前算法等一系列算法，可以将点云构造得到不规则三角网TIN模型。而模型表面纹理则是通过倾斜影像自动纹理映射得到。得到的重建结果需要裁剪，其目的主要是将模型的边缘部分裁去以便拼接。

裁剪后的模型通过单点对齐拼接为完整的缆索模型。其具体操作为：a) 在待拼接的两个模型上找到一组纹理结构相对应的点。b) 在保证对应点重合的情况下将两个模型尽可能贴合。重复完成该过程就可以将四个模型拼接完成。得到结果如图4所示，其中两张图分别为不同角度下的模型。由图4可以看出，本文提出的方法能够重建得到纹理清晰，失真较少的三维模型。

Figure 4. Diagram of mosaicked model

图4. 拼接模型图

4. 结果分析及几何精度评定

图5以及图6展示了Block3，Block4 (可参见3.2)校正前后的模型。图中左为校正前模型，右为校正后模型。可以看出校正前的模型存在弯曲失真的情况，与缆索的实际情况不符；而校正后的模型大大减少了这种失真，提高了重建模型的精度。

接下来对模型的几何精度进行评估。评定该模型的几何结构精度需要将模型各个位置上的直径与真实缆索直径进行比对，直径差值的大小将会作为模型精度的指标。

直径测量位置可参见图7，图中所示ABCD四点是选定测量直径的位置。根据人工吊篮的方式，测量得到真实的桥梁缆索直径，四个点的直径分别为111.4 mm、110.8 mm、110.7 mm、111.1 mm。根据爬索机器人重建得到的模型的直径可由点云处理软件(CloudCompare)测量得到。软件中可以显示的位数较多，为了保证精度将数据保留到小数点后三位。所有测量所得结果如表2直径测量结果所示，根据该数值可以分别计算得到选定点直径的相对误差以及平均绝对误差。

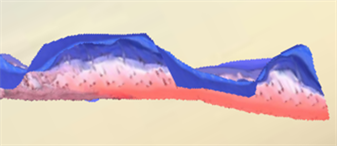
Figure 5. Diagram of the comparison before and after distortion correction of Block3. The left diagram shows the model before distortion correction, and the right diagram shows the model after distortion correction

图5. Block3畸变校正前后对比。左图为校正前的模型，右图为校正后的模型

Figure 6. Comparison before and after distortion correction of Block4. The left diagram shows the model before distortion correction, and the right diagram shows the model after distortion correction

图6. Block4畸变校正前后对比。左图为校正前的模型，右图为校正后的模型

Figure 7. Diagram of the measurement position

图7. 测量位置图

Table 2. Diameter measurement results

表2. 直径测量结果

5. 结论

1) 本文基于被动式三维重建原理，针对桥梁缆索的三维重建提出了一种仅使用影像数据来重建缆索的三维数字模型的重建流程。经实验验证，该方法可以得到纹理清晰，几何精度高的三维数字模型。

2) 本文提出的重建流程可以降低数据获取成本。通过构造POS数据来实现POS辅助空中三角测量。这种方式没有使用地面控制点，节省了数据获取的成本。建模过程中采用四个方向分别建模再拼接的形式，降低了数据获取中对于多角度需求。

3) 本文在数据处理过程中使用单参数除法模型对图片进行了畸变矫正，减少了径向畸变带来的模型失真，进一步提高了重建模型的精度。

基金项目

国家自然科学基金资助项目(U21A20139)。