1. 引言
水声波的传播特性对于极地海洋环境中的水下目标探测、地震引发海啸的机理研究和预警机制具有重要影响。目前,关于线性水声波的传播特性研究已有了大量的重要成果。然而,在极地特殊海洋环境中存在着大面积冰层覆盖、垂向密度分层和底部粘性等复杂因素,非线性水声波在这些环境中的传播特性、衰减、反射和吸收机制等问题仍然是未解决的关键科学问题,而且对于极地环境中的海洋资源探测、水下目标探测、海底地震和海啸预警具有重要的参考价值。
Mikhin和Morozov (2008) [1] 分析了线性水声波在冰盖覆盖下的传播特性。S. Michele (2020) [2] 等人利用线性薛定谔方程来描述大的时空间尺度上水声波的传播特性。Zhang等(2015) [3] 对冰洋环境中水声波传播进行了数值模拟和理论分析。刘亚东(2022) [4] 探究表面弹性冰层与受扰动影响的可压缩流体之间的声弹性问题,利用Green函数得到波形的积分形式解。线性模型将海洋中的冰层视为弹性板,并运用水弹性理论来分析波浪作用下冰层的响应。这种线性模型在描述水声波与冰层的相互作用行为方面提供了有价值的结果。它能够有效预测波浪在冰层上的传播特性,并为水声工程设计和应用提供重要的参考。
然而,线性模型对实际海况不再适用。首先,线性模型仅考虑了波浪和冰层之间的线性相互作用。在复杂的海洋环境中,大振幅波浪和孤立波等非线性效应可能对冰层的响应产生显著影响。其次,线性模型在考虑冰层的复杂情况方面有所限制。实际的冰层可能具有不均匀的厚度、刚度和密度分布,也可能存在断裂、缝隙以及部分融化等复杂情形。现有的线性模型很难描述这些复杂的冰层特征。
因此,研究非线性水声波问题对于更准确地预测冰层的行为和保证工程的可靠性具有重要意义。张世功等人(2016) [5] 针对一维非线性水声波传播问题进行了有限元仿真和实验研究,推导了一维非线性声波方程的有限元形式;此外,Yang (2018) [6] 首次利用同伦分析方法(HAM)对声重力波的稳态共振三元相互作用进行了非线性解析近似方法的研究。研究发现,共振水声波引起的海底微震较非共振情况下所引起的海底微震更大。Kadri (2016) [7] 对非线性声重力波三元共振的时间反转类比进行了研究;最近,Kadri和Wang (2021) [8] 在柱坐标下研究了声重力波非线性三元相互作用的近似解,将Yang的结论扩展到了三维范围。除了共振现象,水声波也可以由海底地震引发。胡晨彤(2020) [9] 推导出海底振动与海水运动之间关系的理论解,并通过使用ADINA计算结果和测量的地震数据验证了这个理论解。Abdolali、Kadri和Parsons (2018) [10] 等学者研究了水声波在深度变化的水中传播时底部压力和色散关系的变化。
本文通过考虑有限深单层无粘无旋弱可压流体和在水面上覆盖无限长弹性板的情况,建立波动方程以及控制方程和边界条件。在已有的线性色散关系的基础上,通过引入一个参数来修正色散关系,从而得到一种近似的非线性色散方程,并进一步详细分析了实际极地海洋环境中水声波的传播特性,包括频率差异和非线性增强的影响,从而对极地海洋资源的探测、地震引发海啸机理的研究和预警机制的改进具有重要意义。
2.数学模型
建立如图1直角坐标系oxz,其中oz轴以垂直向上为正,ox轴与静止时水面重合,水平向右为正。厚度为d的无限长弹性板漂浮在水面上,吃水为0。假设有限深流体是无粘的、可压的且流动是无旋的,则速度势
满足波动方程
(1)
其中
为Laplace算子,c为流体中的声速,t为时间,h为流体深度。
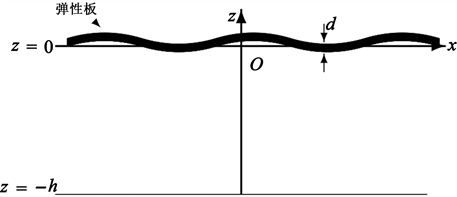
Figure 1. Coordinate diagram of nonlinear interaction between underwater sound and infinite elastic plate in a single layer fluid
图1. 单层流体中水声与无限长弹性板的非线性相互作用坐标示意图
在弹性板和流体交界的表面
,运动学边界条件和动力学边界条件分别为
(2)
(3)
其中g是重力加速度,
是板下表面压力,
为流体密度。假设弹性板是均匀的薄弹性材料,且流体和板不分离。
在流体底部,根据固壁的非渗透条件有
(4)
3. 近似的非线性色散关系
给定
,Abdolali、Kadri和Parsons [10] 等人得到线性色散关系如下
(5)
其中
为水声波的频率,
为水声波的波数,T为侧向应力,
为弹性板的密度。
在复杂的海洋环境中,大振幅波浪的非线性效应对水声波的传播产生显著影响,真实的波频率
与线性波频率
存在偏差,为较准确地描述非线性水声波在复杂海洋环境中的传播特性,本文引入
(6)
其中
是一个略大于1的常数。
增大时,水声波的非线性增强。
将(6)代入(5)得
(7)
给定常数
的值,公式(7)是一个f关于
的复杂超越方程,直接求得f与
的色散关系比较困难,我们需要对公式(7)做一些变换。
根据Abdolali、Kadri和Parsons [10] 等人的工作,我们引入
(8)
它解释了重力相对于弹性板振动的影响。当
时,有
,
令
(9)
是一个无限接近于0的量。
色散方程变为
(10)
整理得
(11)
对方程(11)进行
麦克劳林级数展开并保留主导项,整理后色散关系变为:
(12)
又由(9)得
(13)
由于色散方程(13)的右端是一个关于
的偶函数,所以本文仅考虑正轴的情况。由
知,当
(N为某个正整数)时,有
,则
是实数,对应N个水声波模态的波数。
令
,代入色散方程(11)可以得到水声波的波数频率关系。
首先,考虑
对水声波传播特性的影响。分别取
与
,代入色散方程(11),得到水声波的波数–频率关系(见图2~5),可见同频率下水声波波数随着
的增大而逐渐增大;频率较低时
对水声波波数的影响较大,频率较高时
对水声波波数敏感度较小。而且,频率较低时波数随频率变化较慢,频率较高时波数随频率变化较快。而且,从这些图中可以看出,我们的结果与Abdolali、Kadri和Parsons [10] 等人得到的线性色散关系结果大体一致,近似非线性色散关系就是对该线性色散关系线性修正后获得,从而说明我们的结论是准确的和科学的。
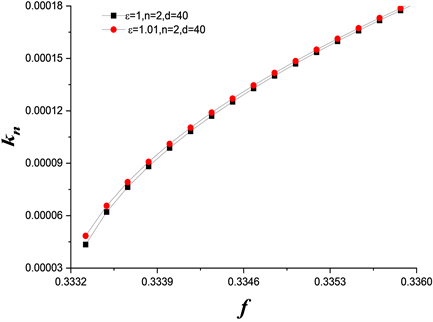
Figure 2. Wave number-frequency relation of the second mode hydroacoustic wave when the thickness of the elastic plate is 40 meters
图2. 弹性板厚度为40 m时第二模态水声波的波数–频率关系

Figure 3. Wave number-frequency relation of the second mode hydroacoustic wave when the thickness of the elastic plate is 60 meters
图3. 弹性板厚度为60 m时第二模态水声波的波数–频率关系

Figure 4. Wave number-frequency relation of the third mode hydroacoustic wave when the thickness of the elastic plate is 40 meters
图4. 弹性板厚度为40 m时第三模态水声波的波数–频率关系

Figure 5. Wave number-frequency relation of the third mode hydroacoustic wave when the thickness of the elastic plate is 60 meters
图5. 弹性板厚度为60 m时第三模态水声波的波数–频率关系
其次,考虑弹性板d对水声波传播特性的影响。基于上述色散方程表示的色散关系,分别取弹性板厚度为
,取
,得到水声波的波数–频率关系(见图6、图7),对于水声波前三阶模态,在频率较低时,随着板厚度的增加,同一频率下的波数会增加,这意味着波长随着板厚度的增加而缩短,这时波的传播受到弹性板厚度的影响较大;在频率较高时,弹性板厚度对波的传播的影响逐渐减小,这意味着随着频率的增加,波数的变化对弹性板厚度的敏感性减弱。
最后,考虑水声波模态对传播特性的影响,分别取水声波模态为
,
,
和
。得到水声波模态对传播特性的影响(见图8、图9)。对于水声波前三阶模态,随着模态增大,同一频率下的波数会减小;频率较低时,不同模态对应的波数间差异较大,随着频率增大,这种差异逐渐减小,可见在频率较低时,同频率下波数受模态的影响较大,而在频率较高时,同频率下波数受模态的影响较小。
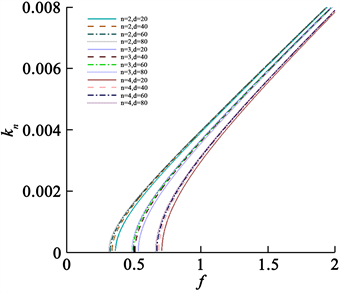
Figure 6. Wave number-frequency relation of water acoustic wave when
图6.
时水声波的波数–频率关系
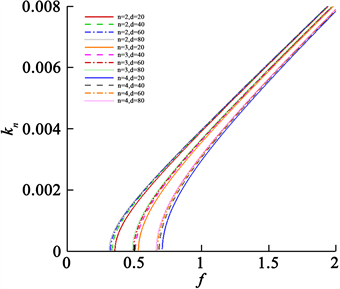
Figure 7. Wave numbe-frequency relation of water acoustic wave when
图7.
时水声波的波数–频率关系

Figure 8. Influence of water acoustic wave modes on propagation characteristics for
图8.
时水声波模态对传播特性的影响
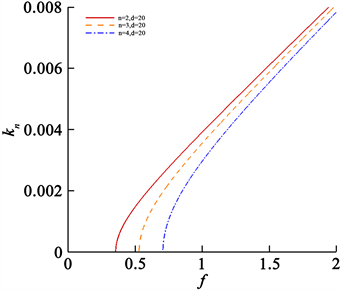
Figure 9. Influence of water acoustic wave modes on propagation characteristics for
图9.
时水声波模态对传播特性的影响
4. 结论
在势流理论的框架下,本文研究了无限长弹性板覆盖下的有限深可压单层流体中非线性水声波的色散关系。主要结论如下:
1) 非线性影响:引入一个参数来修正线性色散关系,以考虑大振幅波浪对水声波的非线性影响。频率较低时
对水声波波数的影响较大,频率较高时
对水声波波数影响较小。
2) 弹性板厚度影响:通过分析弹性板厚度对水声波传播特性的影响,发现弹性板的厚度增加会导致同一频率下的波数增加。在高频率下,波的传播受到冰层厚度的影响相对较小,其他因素可能更加显著地影响波的传播行为。
3) 水声波模态影响:研究了不同水声波模态对传播的影响。发现随着模态增加,同频率下的波数减小,频率较低时模态变化对波数影响较大,而高频时影响较小。
这些研究结果对于理解非线性水声波在复杂海洋环境中的传播特性具有重要意义。这不仅对极地海洋资源的探测、地震引发海啸的机理研究和预警机制的改进提供了参考,还为工程应用中的水声传播提供了理论指导。未来的研究可以进一步探讨更多复杂环境中的非线性水声波传播特性,以更全面地揭示其行为和影响。
NOTES
*通讯作者。