1. 引言
纽结(链环)多项式是一个纽结不变量,且是以系数符合给定纽结(链环)性质的多项式。其中重要的纽结多项式有:Alexander,Alexander-Conway,Jones多项式等,其均为定向纽结和链环的单变量Laurent多项式不变量。HOMFLY多项式是定向纽结和链环的双变量Laurent多项式不变量。Kauffman多项式F是纽结和链环的双变量的半定向多项式不变量,他可以更好地区分纽结(链环)和他的镜像。根据纽结或链环的Kauffman多项式F可以得出该纽结或链环的Jones多项式和BLM/Ho多项式等。Kauffman多项式F的原始版本是不定向纽结和链环图的正则合痕不变量,用L表示。
2014年,Berceanu B,Nizami A R利用简单递归关系,给出计算闭辫子Jones多项式的新方法,得出Jones多项式的一般展开式和有理生成函数 [1] 。2015年,Duzhin S,Shkolnikov M给出有理链环(纽结) HOMFLY多项式的详细公式 [2] 。Taşköprü K,Altıntaş İ研究了作为广义Fibonacci多项式的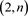 环面链环的HOMFLY多项式,给出
环面链环的HOMFLY多项式,给出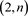 环面链环的HOMFLY多项式和广义的Fibonacci多项式之间的矩阵表示 [3] 。2018年,Ismet Altintas,Kemal Taşköprü,Merve Beyaztaş证明环面链环的尖括号多项式的递归关系式与Fibonacci多项式相似,给出其一些基本性质 [4] 。2019年,Altıntaş İ,Taşköprü K研究了可以作为Fibonacci类型多项式的
环面链环的HOMFLY多项式和广义的Fibonacci多项式之间的矩阵表示 [3] 。2018年,Ismet Altintas,Kemal Taşköprü,Merve Beyaztaş证明环面链环的尖括号多项式的递归关系式与Fibonacci多项式相似,给出其一些基本性质 [4] 。2019年,Altıntaş İ,Taşköprü K研究了可以作为Fibonacci类型多项式的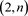 环面链环的Kauffman多项式和BLM\Ho多项式,借助BLM\Ho多项式来解释Kauffman多项式 [5] 。在此基础上,本文研究了一类n分支不定向直线型链环和复叠链环,并计算其Kauffman多项式。为实现此类链环Kauffman多项式的计算,第一部分介绍了纽结理论相关的基础知识和基本概念;第二部分计算n分支直线型链环的Kauffman多项式;第三部分借助n分支直线型链环的Kauffman多项式计算n分支复叠链环的Kauffman多项式。
环面链环的Kauffman多项式和BLM\Ho多项式,借助BLM\Ho多项式来解释Kauffman多项式 [5] 。在此基础上,本文研究了一类n分支不定向直线型链环和复叠链环,并计算其Kauffman多项式。为实现此类链环Kauffman多项式的计算,第一部分介绍了纽结理论相关的基础知识和基本概念;第二部分计算n分支直线型链环的Kauffman多项式;第三部分借助n分支直线型链环的Kauffman多项式计算n分支复叠链环的Kauffman多项式。
2. 预备知识
2.1. 纽结与链环
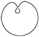
[6] 纽结:设K为S3中的一个简单闭曲线,且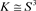 ,则称K为一个纽结,如果给定K一个定向,则称K为一个定向纽结。图1为平凡结。
,则称K为一个纽结,如果给定K一个定向,则称K为一个定向纽结。图1为平凡结。
[7] 链环:将若干个互不相交的圆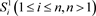 嵌入到三维欧氏空间R3中,这些圆形成的空间图称为链环,记
嵌入到三维欧氏空间R3中,这些圆形成的空间图称为链环,记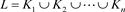 ,每个纽结
,每个纽结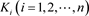 为链环L的一个分支,在此之中n为链环L的分支数。如果给每个链环的每一个分支一个固定的方向,则称这个链环为一个定向链环。
为链环L的一个分支,在此之中n为链环L的分支数。如果给每个链环的每一个分支一个固定的方向,则称这个链环为一个定向链环。
[6] 注1:纽结为分支数为1的链环。
[6] 注2:若链环L所有的分支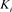 都是平凡结,则称链环L为平凡链环。如图2所示。
都是平凡结,则称链环L为平凡链环。如图2所示。
2.2. [8] 纽结(链环)的投影图
对于一个纽结(链环),选取一个合适的平面,选择一个合适的方向对其进行投影,把三维空间中的纽结(链环)正则投影到这个平面上,得到的投影图中只有有限多个交叉点;每个交叉点都是二重点,在上下线处的投影都是互相穿越交叉的。则称其为纽结(链环)投影图。
注:投影图会因为选取平面的不同而不同。
2.3. [9] [10] Reidemeister Move (R变换)
R变换是纽结理论中最基本的变换,它可以概括三维空间中纽结所有的拓扑情形。R变换是改变纽结的正则投影图的三种方式,其中每一种方式都会改变交叉点之间的关系。Reidemeister变换有三种变换方式,分别为R1变换、R2变换、R3变换。如图3所示。
2.4. [11] 纽结的分离并
在链环L的补空间 中,存在一个二维球面S,将其嵌入可以将链环L分为不同的连通分支,并且这两个分支分布在球面S的两侧,则称链环L为可分离的。如果将所得的这两个不同的连通分支记为
中,存在一个二维球面S,将其嵌入可以将链环L分为不同的连通分支,并且这两个分支分布在球面S的两侧,则称链环L为可分离的。如果将所得的这两个不同的连通分支记为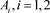 ,则此时
,则此时 ,称L为L1和L2的分离并,记作
,称L为L1和L2的分离并,记作 。
。
2.5. [5] Kauffman多项式 定义
定义
Kauffman多项式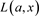 是不定向链环投影图K的一个双变量的Laurent多项式,Kauffman多项式
是不定向链环投影图K的一个双变量的Laurent多项式,Kauffman多项式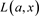 是链环K的合痕不变量。并且Kauffman多项式
是链环K的合痕不变量。并且Kauffman多项式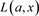 的特殊化是链环的尖括号多项式,其也是BLM/Ho多项式的双变量推广。
的特殊化是链环的尖括号多项式,其也是BLM/Ho多项式的双变量推广。
2.6. [5] Kauffman多项式 的计算满足如下几个规则
的计算满足如下几个规则
1) 
其中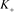 、
、 、
、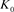 、
、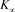 是如图4所示的不定向图。
是如图4所示的不定向图。
2) ,其中O为平凡结。
,其中O为平凡结。
3)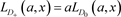 。
。
4) 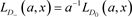
其中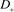 、
、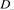 、
、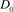 是如图5所示的不定向图。
是如图5所示的不定向图。
2.7. [5] Kauffman多项式 的性质
的性质
1)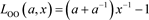 或
或 ,
, ,其中OO为2分支的平凡链环。
,其中OO为2分支的平凡链环。
2) 是一个平凡的m分支链环,
是一个平凡的m分支链环,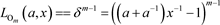 。
。
3)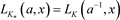 ,其中
,其中 表示链环K的镜像。
表示链环K的镜像。
4)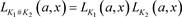 ,其中
,其中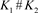 为链环
为链环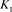 和
和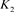 的组合。
的组合。
5)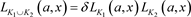 ,其中
,其中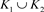 为链环
为链环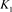 和
和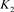 的不相交并。
的不相交并。
3. 一类特殊链环的Kauffman多项式L
n分支直线型链环Ln的Kauffman多项式L(Ln)
[11] 定义3.1 n分支直线型链环Ln:由n个分支所构成,且是由n个平凡结按照特定方式并在一起,如图6所示。
注1:最简单的非平凡的直线型链环为2个分支的直线型链环,即Hopf链环。
注2:规定1分支的直线型链环为平凡结。
[12] 定义3.2 n分支复叠链环Kn:由n个分支构成,是由n个平凡结两两相扣所得。如图7所示。
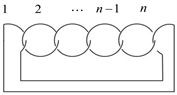
Figure 7. The covering links of n components link Kn
图7. n分支复叠链环Kn
定理3.1 n分支直线型链环Ln,其Kauffman多项式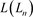 表达式为
表达式为
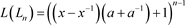 .
.
证明 对于n分支直线型链环Ln,对其左下角交叉点应用Kauffman多项式的拆接关系式,令其生成链环分别为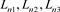 ,如图8所示。
,如图8所示。
即拆接关系式为
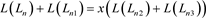 ,
,
其中链环 为平凡结与
为平凡结与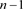 分支直线型链环
分支直线型链环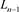 的并;对
的并;对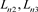 应用一系列R1变换得到链环
应用一系列R1变换得到链环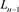 。可以得到如下关系式
。可以得到如下关系式
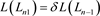 ,
,
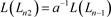 ,
,
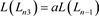 .
.
即拆接关系式等价于
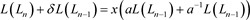 ,其中
,其中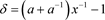
对其进行整理,得到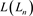 的递归关系式
的递归关系式
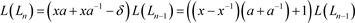 ,
,
则有
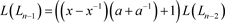 ,
,
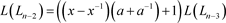 ,
,

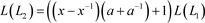
由于L1为1分支的直线型链环,为平凡结,则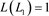 。
。
对上述等式进行合并整理,有
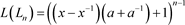 .
.
定理得证。
定理3.2 n分支复叠链环Kn的Kauffman多项式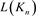 的递归关系式为
的递归关系式为
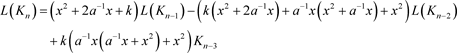
初值为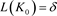 ,
,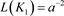 ,
,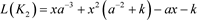 ,其中
,其中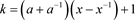 。
。
证明 下面对一类不定向n分支复叠链环Kn的Kauffman多项式进行研究,首先对链环Kn左上角的交叉点应用Kauffman多项式的拆接关系式,令其生成的三个链环分别为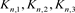 ,拆接关系式如图9所示。
,拆接关系式如图9所示。
即拆接关系式为
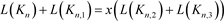 (3.1)
(3.1)
而对链环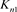 应用一系列R2变换,其可看作n分支直线型链环Ln;对链环
应用一系列R2变换,其可看作n分支直线型链环Ln;对链环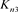 应用一系列R1变换,其可看作
应用一系列R1变换,其可看作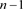 分支复叠链环
分支复叠链环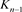 。
。
则3.1式等价于
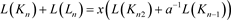 . (3.2)
. (3.2)
观察发现, 为
为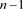 分支链环,令其为
分支链环,令其为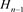 。接着对链环
。接着对链环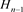 左上角的交叉点A应用Kauffman多项式的拆接关系式,令其所生成的链环分别为
左上角的交叉点A应用Kauffman多项式的拆接关系式,令其所生成的链环分别为 ,拆接关系如图10所示。
,拆接关系如图10所示。
即拆接关系式为
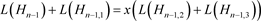 , (3.3)
, (3.3)
而对链环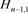 应用一系列R1、R2变换,其可看作
应用一系列R1、R2变换,其可看作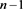 分支直线型链环
分支直线型链环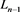 ;对链环
;对链环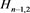 应用一系列R1变换,其可看作
应用一系列R1变换,其可看作 分支链环
分支链环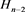 ;链环
;链环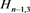 为
为 分支链环,令其为
分支链环,令其为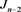 。
。
则3.3式等价于
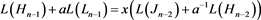 . (3.4)
. (3.4)
下面对 分支的链环
分支的链环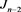 的Kauffman多项式进行研究,对链环
的Kauffman多项式进行研究,对链环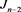 的交叉点B应用Kauffman多项式的拆接关系式,令其生成的链环分别为
的交叉点B应用Kauffman多项式的拆接关系式,令其生成的链环分别为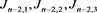 ,如图11所示。
,如图11所示。
即拆接关系式为
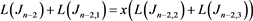 , (3.5)
, (3.5)
而对链环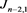 应用一系列R2变换,其可看作
应用一系列R2变换,其可看作 分支复叠链环
分支复叠链环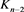 ;对链环
;对链环 应用一系列R1变换,其可看作
应用一系列R1变换,其可看作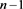 分支直线型链环
分支直线型链环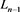 ;链环
;链环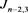 为
为 分支链环
分支链环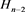 。
。
则3.5式等价于
 . (3.6)
. (3.6)
对3.2、3.4、3.6式进行合并、整理,可得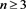 时,Kn的Kauffman多项式
时,Kn的Kauffman多项式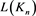 的递归关系式为:
的递归关系式为:
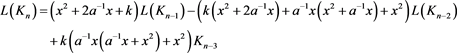 (3.7)
(3.7)
初值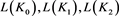 的计算分别如下:
的计算分别如下:
1) 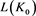
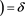

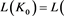 .
.
2) 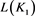
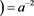
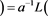
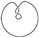
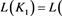 .
.
3) 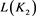
对链环K2的左上方的交叉点应用Kauffman多项式的拆接关系式,令生成的链环分别为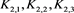 ,如图12所示。
,如图12所示。
则有如下表达式

而对链环 应用一系列R2变换,其可看作2分支直线型链环L2;对链环
应用一系列R2变换,其可看作2分支直线型链环L2;对链环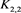 应用一系列R1变换,其可看作1分支链环L1。
应用一系列R1变换,其可看作1分支链环L1。
即
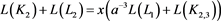 (3.8)
(3.8)
接着对链环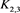 的右上方的交叉点应用Kauffman多项式的拆接关系式,令其生成的三个链环分别为
的右上方的交叉点应用Kauffman多项式的拆接关系式,令其生成的三个链环分别为 ,拆接关系式如图13所示。
,拆接关系式如图13所示。
则有
而对链环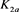 应用一系列R1、R2变换,其可看作平凡结;对链环
应用一系列R1、R2变换,其可看作平凡结;对链环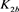 应用一系列R1变换,其可看作平凡结。即
应用一系列R1变换,其可看作平凡结。即
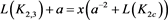 (3.9)
(3.9)
接着对链环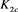 的左侧的交叉点应用Kauffman多项式的拆接关系式,令其生成的链环分别为
的左侧的交叉点应用Kauffman多项式的拆接关系式,令其生成的链环分别为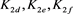 。如图14所示。
。如图14所示。
则有如下表达式
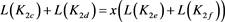
而对链环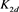 应用一系列R2变换,其可看作两个平凡结的并;对链环
应用一系列R2变换,其可看作两个平凡结的并;对链环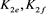 应用一系列R1变换,其可看作平凡结。即
应用一系列R1变换,其可看作平凡结。即
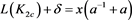 (3.10)
(3.10)
对3.8~3.10式进行合并整理,得到链环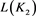 的表达式为:
的表达式为:
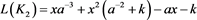
其中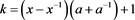 。
。
综上所述,定理得证。
注:全文k均为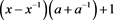 。
。
定理3.3 n分支复叠链环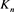 的Kauffman多项式
的Kauffman多项式 所对应特征多项式的特征根为
所对应特征多项式的特征根为
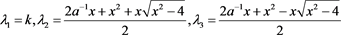
其中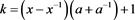
证明 由定理3.2可知,链环Kn的Kauffman多项式的递归关系式为
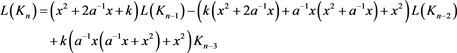
则其对应的特征多项式为
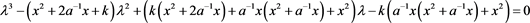
即
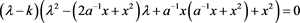
则该特征多项式的三个特征根分别为
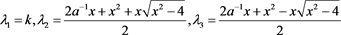 .
.
定理得证。
推论3.4 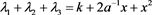
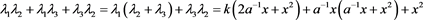
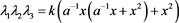
其中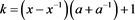
证明 将 、
、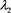 、
、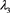 的值带入即可得到。
的值带入即可得到。
性质3.5 序列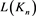 对应的生成函数为
对应的生成函数为
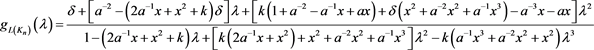
其中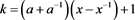 。
。
证明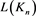 的生成函数的形式如下:
的生成函数的形式如下:
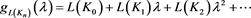
分别对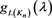 乘以
乘以
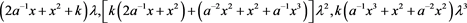
则有
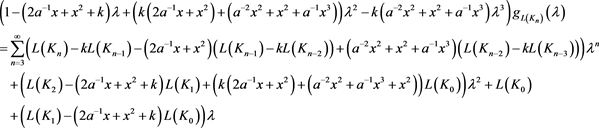
由序列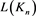 的递归关系式可知
的递归关系式可知
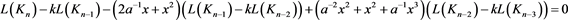 ,
,
则
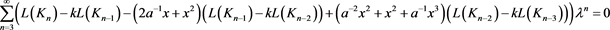
则原式等价于
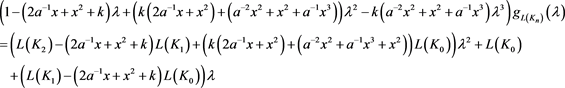
将三个初值 、
、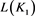 、
、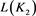 的值依次代入上述等式,即可得到序列
的值依次代入上述等式,即可得到序列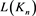 所对应的生成函数为
所对应的生成函数为
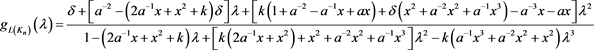
命题得证。
定理3.6 序列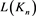 的通解为
的通解为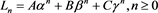 ,其中
,其中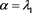 ,
,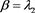 ,
,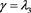
其中
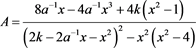

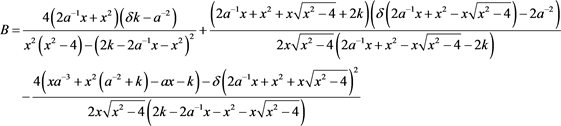
其中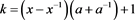
证明 序列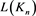 的通项公式为
的通项公式为
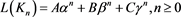
则分别令 ,有
,有
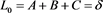 (1)
(1)
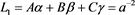 (2)
(2)
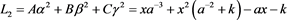 ,其中
,其中 . (3)
. (3)
解系数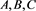 分别如下:
分别如下:
首先对系数C进行求解。对(1)式分别左右乘以 、
、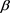 、
、 有(4)式,对(1)式分别左右乘以
有(4)式,对(1)式分别左右乘以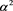 、
、 、
、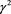 有(5)式。
有(5)式。
则有如下等式
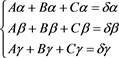 (4)
(4)
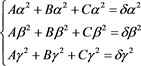 (5)
(5)
则将上述(4)、(5)两式分别与(2)、(3)式作差,有(6)式和(7)式:
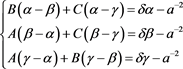 (6)
(6)
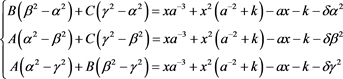 (7)
(7)
对上述(6)、(7)两式进行合并整理,得到C的表达式为:
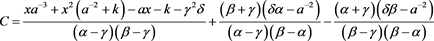
同理可以求出

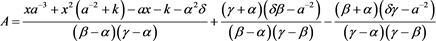
将 、
、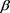 、
、 的值带入上述三个式子即可得到
的值带入上述三个式子即可得到
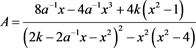
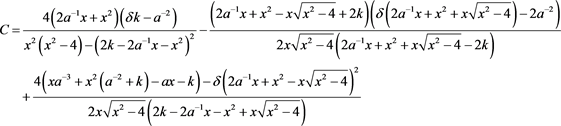

定理得证。
4. 结语
本文主要研究一类特殊不定向链环——复叠链环的Kauffman多项式。借助直线型链环的Kauffman多项式对复叠链环的Kauffman多项式进行研究。利用Kauffman多项式的拆接关系式推出其递归关系式,进而研究了这个递归关系式的生成函数。为研究定向复叠链环的Kauffman多项式以及BLM/Ho多项式奠定基础。