1. 引言
如今,随着岩石力学的研究不断的发展,对岩石的内部需要更加深层次的研究。一般岩石内部都存在着岩石裂隙、节理等像不连续的岩石内部特性,给岩石性质研究者带来了许多的问题和困难。在实验室里面,对岩石内部预制裂隙同时还要观察到其压缩时裂纹扩展具有一定的困难。如果使用一些相近的材料来进行模拟也是很难模拟出岩石内部的黏结特性,同时很难模拟出真实的裂纹扩展规律。随着颗粒流数值模拟的技术的发展,离散元的数值模拟在国际学术上也得到认可。通过PFC2D中自带的颗粒粘结模型更容易模拟出岩石内部黏结关系,还可以在微观上进行对岩石力学的研究。
目前越来越多的学者开始对裂隙岩石进行学术研究,裂隙岩石是岩土工程中最基础的岩石试样,而裂隙的存在往往可能会给岩土工程带来严重的后果,如岩石爆破、崩塌等等。黄达等 [1] 研究以中等加载速率的单轴压缩对不同倾角裂隙砂岩试样的影响规律。Yang Sheng-Qi等 [2] 通过对单裂隙砂岩进行单轴实验,发现裂隙的长度以及角度会影响砂岩的最终的破坏模式的参数。王煜等 [3] 研究了加载速率、裂隙倾角两个复合因素对单裂隙岩石的力学性质的影响规律。张顺金 [4] 研究裂隙角度、裂隙数量两个复合因素对岩石的抗压强度的影响。尹成薇 [5] 研究了不同位置、不同排列方式以及不同的加载速率对裂纹扩展的贯通规律。Wong等 [6] 通过对双裂隙大理岩试样进行单轴压缩实验,研究分析抗压强度和裂纹扩展规律。蒲成志等 [7] 研究2条预制裂隙在单轴压缩下的贯通以及破坏的规律。Zhang等 [8] 通过对单裂隙的进行单轴压缩实验,研究了裂纹的扩展时应力变化规律。本文研究岩石裂隙的存在能否会影响岩石的抗压强度,利用PFC2D对岩石进行压缩实验,分析有无裂隙对岩石的抗压强度的影响以及裂隙的角度能否影响岩石抗压强度和新产生的裂纹。
2. PFC2D数值模拟
2.1. PFC2D数值模拟方案
PFC2D中模拟岩石试样模型,利用PFC2D中Command以及其中内嵌的Fish语言编写生成四个墙壁,形成一个一定区域的矩形,形成边界控制。同时使用随机分布颗粒生成方法中按照孔隙比生成方法生成颗粒,其中颗粒的粒径有着不同的尺寸,并在无摩擦的状态下运行一定的时步完成,使得到的颗粒集合体是一个均匀密集的集合体。之后在颗粒之间添加胶结,使得颗粒与颗粒之间有着一定的胶结力,以模拟颗粒之间的接触。对于裂隙岩石的模拟,为了接近真实岩石的情况,根据相关文献和资料查阅,选择采用花岗岩的试样数据进行模拟 [9] 。在PFC2D中生成一个长 × 宽为100 mm × 60 mm的块状模型,模型中颗粒相关细观参数如表1所示。
2.2. 颗粒接触模型
PFC中的颗粒是刚性颗粒,颗粒之间的胶结关系模拟颗粒之间的接触力,而颗粒与颗粒之间遵循的是牛顿第二定律。颗粒之间的破坏形式只有剪切和张开两种形式,当颗粒之间的关系发生了变化,则会影响试样的宏观面上的力学性质。颗粒之间的接触模型中最常用的是接触黏结模型和平行黏结模型,本文实验使用平行黏结模型。当平行黏结模型在黏结处在拉伸、剪切应力等情况下发生破坏后,会退化为线性模型;而且平行黏结模型对模型试样在受压和受拉情况下都起作用,其中线性接触部分只会受压情况下起作用。当颗粒之间的关系发生了变化,则会影响试样的宏观面上的力学性质。因此,不需要给试样的宏观本构模型定义对应的参数,只需要对试样的颗粒定义一些几何和力学参数,如刚度、摩檫力、模量等等,如表2所示。
 (a) 图是无裂隙的完整岩石模型;(b) 图是裂隙倾角为0˚的岩石模型;(c) 图是裂隙倾角为30˚的岩石模型;(d) 图是裂隙倾角为60˚的岩石模型;(e) 图是裂隙倾角为90˚的岩石模型。
(a) 图是无裂隙的完整岩石模型;(b) 图是裂隙倾角为0˚的岩石模型;(c) 图是裂隙倾角为30˚的岩石模型;(d) 图是裂隙倾角为60˚的岩石模型;(e) 图是裂隙倾角为90˚的岩石模型。
Figure 1. Initial model of rock
图1. 岩石的初始模型
 (a) 图是无裂隙模型单轴压缩破坏结果;(b) 图是裂隙倾角0˚模型单轴压缩破坏结果;(c) 图是裂隙倾角30˚模型单轴压缩破坏结果;(d) 图是裂隙倾角60˚模型单轴压缩破坏结果;(e) 图是裂隙倾角90˚模型单轴压缩破坏结果。
(a) 图是无裂隙模型单轴压缩破坏结果;(b) 图是裂隙倾角0˚模型单轴压缩破坏结果;(c) 图是裂隙倾角30˚模型单轴压缩破坏结果;(d) 图是裂隙倾角60˚模型单轴压缩破坏结果;(e) 图是裂隙倾角90˚模型单轴压缩破坏结果。
Figure 2. Failure results of rock uniaxial compression
图2. 岩石单轴压缩的破坏结果
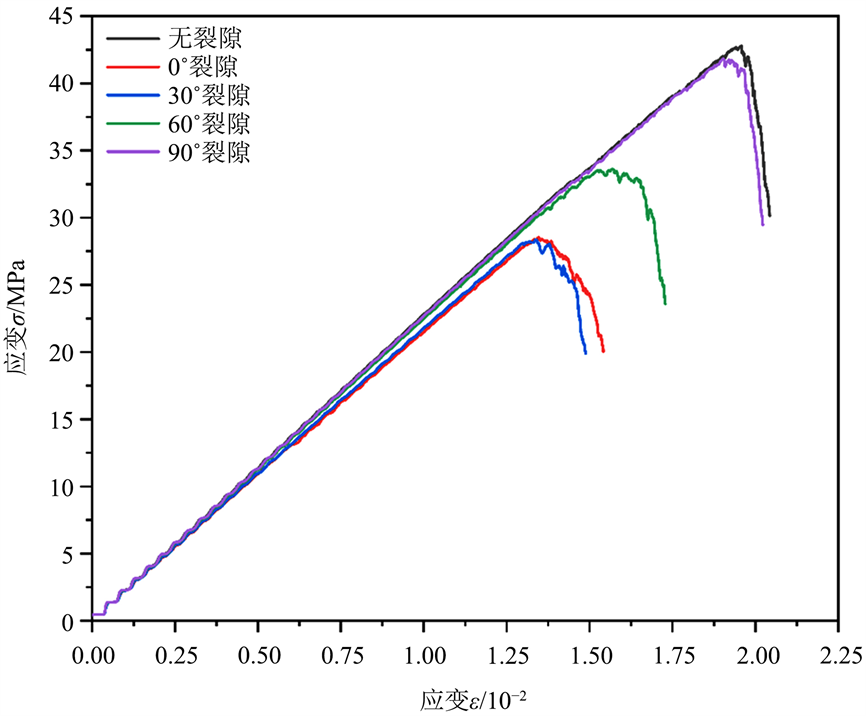 (a) 图是无裂隙模型单轴压缩应力–应变曲线图;(b) 图是裂隙倾角0˚模型单轴压缩应力–应变曲线图;(c) 图是裂隙倾角30˚模型单轴压缩应力–应变曲线图;(d) 图是裂隙倾角60˚模型单轴压缩应力–应变曲线图;(e) 图是裂隙倾角90˚模型单轴压缩应力–应变曲线图。
(a) 图是无裂隙模型单轴压缩应力–应变曲线图;(b) 图是裂隙倾角0˚模型单轴压缩应力–应变曲线图;(c) 图是裂隙倾角30˚模型单轴压缩应力–应变曲线图;(d) 图是裂隙倾角60˚模型单轴压缩应力–应变曲线图;(e) 图是裂隙倾角90˚模型单轴压缩应力–应变曲线图。
Figure 3. Uniaxial compressive stress-strain curve of rock model
图3. 岩石模型单轴压缩应力–应变曲线图
2.3. 预制裂隙
预制裂隙即在数值模拟出的试样中预制裂隙的位置处删除一定范围的颗粒,实验中将裂隙中心在试样模型的几何中心处。实验中预制的裂隙长度为10 mm,宽度为0.5 mm,同时裂隙的倾斜角度设为0˚、30˚、60˚、90˚,这四种情况代表着不同裂隙的角度倾斜程度,如图1所示,以此来对比分析裂隙的存在对岩石的抗压强度的影响。
2.4. 数值模拟实验结果
将之前模拟完成的模型中的侧边墙体删除,来模拟实验中试样无围压或者围压很小的情况,留下垂直方向上的两面墙,使其作为加载板,然后对模型进行单轴压缩实验。对上下的墙体赋予一定的载荷,使得上下两面墙体以0.2 m/s速度相反方向运动进行压缩实验,当应力过了峰值降至70%时,停止实验并列出峰值应力,实验结果如图2所示。并将单轴压缩过程中模型的应力–应变曲线进行绘图,如图3所示。
3. 岩石破裂机理分析
3.1. 裂隙周围的应力场
模型内部预制一条长度为2a的裂隙,且模型试样的加载面受到载荷p,预制的裂隙的倾角为
。建立直角坐标系xOy,其中x轴方向为裂隙的方向,而y轴为裂隙的中垂线。如图4所示。
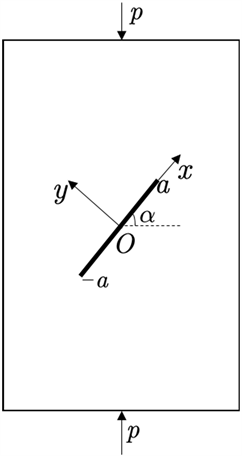
Figure 4. Uniaxially compressed fractured rock specimen
图4. 单轴压缩的裂隙岩石试样
则预制裂隙处的远场应力状态:
(1)
在实验中,由于裂隙面受到压剪的作用,从而产生闭合,因此,裂隙属于Π型裂纹,即
。考虑裂隙面上有摩檫力的存在,因此,裂隙面上受到的等效剪应力为:
(2)
其中:f为裂隙面的摩擦系数,正应力
。
由威斯特嘎德函数
可计算得到裂隙周围的附加应力场为:
(3)
因此,预制裂隙处总的远场应力状态为:
(4)
3.2. 裂纹扩展的方向
裂隙顶端的应力强度因子为:
(5)
将式(2)代入式(5)中,得:
(6)
因为,研究的裂隙是属于Π型裂纹,所以将裂隙的顶端的应力分量用极坐标来表示:
(7)
根据最大周向应力定理,裂纹将会沿着
所对应的
方向扩展。而这个
方向满足:
(8)
由式(7),得:
(9)
(10)
令式(9)等于0,得到:
(11)
最后求出断裂角度为:
(无意义舍去) (12)
将式(12)代入式(10)中,得:
(13)
式(13)小于0是仍然成立。即式(12)解出的
是满足
为最大值的条件,裂纹扩展角
如图5所示。
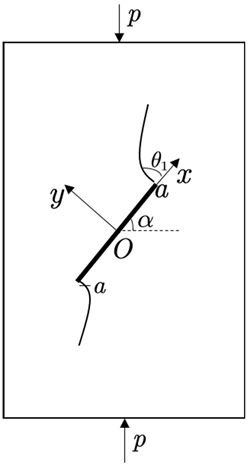
Figure 5. Schematic diagram of crack propagation angle
图5. 裂纹扩展角度示意图
单个裂隙岩体的裂隙起裂扩展形式分为两种:翼型裂纹以及次生裂纹,同时,次生裂纹又分为次生共面裂纹以及次生倾斜裂纹。而这三种裂纹有着不同的破坏类型,其中翼裂纹是属于拉伸型裂纹,次生共面裂纹属于剪切型裂纹,次生倾斜裂纹属于压减型裂纹。裂隙岩体在受到外部载荷不管其载荷是拉伸力还是压缩力,这三种裂纹出现的先后顺序有着不同。翼型裂纹和次生共面裂纹出现的时间会比次生倾斜裂纹早,而最先出现的两种裂纹的时机也会受到裂隙角度的影响。如图6所示,扩展翼型裂纹的方向为裂隙的最大主应力方向,而次生共面裂纹是裂隙扩展贯通速度最快的,次生倾斜裂纹的扩展方向则是垂直于裂隙,会导致其发育缓慢,长度较短,而很多实验证明岩石的破裂行为通常是由次生裂纹扩展贯通而引起的。此外,岩石的围压会影响次生裂纹的产生,在所有具有围压的岩石数值模拟实验中,均能观察到次生共面裂纹的产生,而次生倾斜裂纹仅仅在部分有围压的数值模拟实验中观察到。
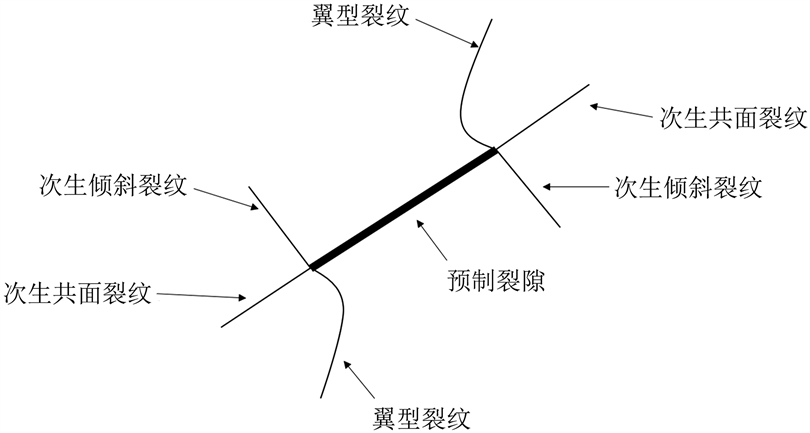
Figure 6. Schematic diagram of crack initiation and propagation of prefabricated cracks
图6. 预制裂隙起裂裂纹扩展的示意图
4. 实验结果与分析
单轴压缩实验中,主要研究岩石在压缩状态下的裂纹扩展特征。在加载压缩过程中,为了让模型试样处于准静态平衡,选择了0.2 m/s的加载速率对模型进行压缩。将实验结果中应力–应变曲线图中应力峰值提取、岩石破坏最终破坏模型中裂纹数量以及模型破坏时的应变处进行统计,数据皆精确到小数点后一位。如表3所示。将各个模型类型的峰值应力即单轴压缩模型的抗压强度做成折线图,更加直观看到各个模型的抗压强度,如图7所示。

Table 3. Data table of numerical simulation
表3. 数值模拟的数据表
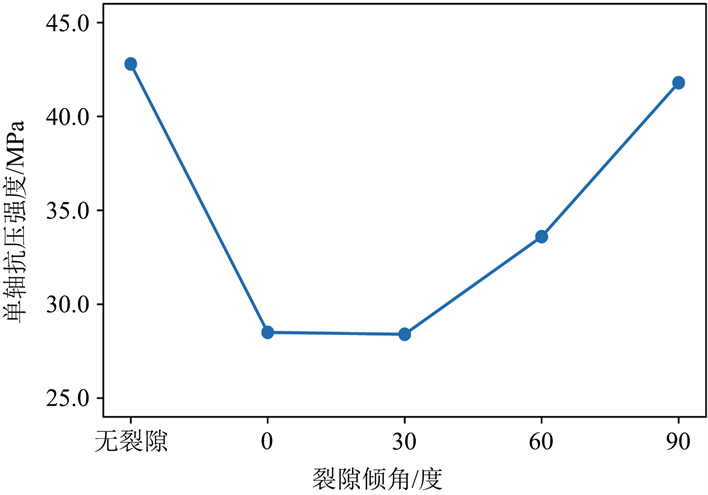
Figure 7. Relationship curve between different model types and uniaxial compression strength
图7. 不同模型类型与单轴压缩抗压强度的关系曲线
1) 根据图7的单轴压缩抗压强度曲线图,可以看出,岩石模型中有无裂隙对其抗压强度有着很大的影响。因为裂隙的存在,在岩石模型受到外部载荷时候,其裂纹产生的位置跟无裂隙模型有所不同。根据图2中岩石模型的最终破坏结果模式分析,对于无裂隙的岩石模型试样进行单轴压缩时,因为岩石内部没有裂隙的存在,随着时间的增加,外部荷载不断上升,试样的加载接触面处会出现应力集中,在试样的上下端会出现裂纹,这些裂纹是属于次生裂纹。随着时间的增加,这些裂纹开始扩展贯通,最后会形成岩石试样的宏观破裂。由图2中图2(b)、图2(c)和图2(d)分析,而相对于有裂隙存在的岩石模型试样,进行单轴压缩时,它会在预先存在的裂隙的两端处产生翼型裂纹,然后会向着加载方向扩展,之后会陆续产生次生裂纹,并且随着时间、荷载的不断增加,次生裂纹以及翼型裂纹的扩展,会逐渐贯通,形成了岩石试样的破裂、崩塌或者剥落。
2) 通过改变预制裂隙的倾角,实验了0˚、30˚、60˚、90˚这四种不同倾角裂隙的岩石模型的抗压强度试验。从所有的最终模型破坏模式可以看出,所有模型的宏观破坏都是张拉劈裂破坏。由图7可知,0˚与30˚倾角的模型试样的抗压强度几乎一致,而随着裂隙的倾角的逐渐增加,岩石试样模型的抗压强度有着明显增加;当裂隙的倾角为90˚时,此时模型的抗压强度跟无裂隙的模型抗压强度接近。相比较图2中图2(c)、图2(d)和图2(e),可以分析出倾斜裂隙会在裂隙的顶端更容易产生应力集中,会导致岩石的抗压强度降低。观察图2中图2(a)和图2(e),二者模型的最终破坏模式大致相同,应力集中点都是在加载接触面。
3) 通过实验过程,以及结果分析,裂隙模型的裂纹产生破坏模式均为剪切变形破坏。裂隙模型由于裂隙顶端应力集中出现了裂纹起裂,然后扩展破坏,通过裂隙模型最终破坏图可以看出,翼型裂纹是最多,而次生共面裂纹以及次生倾斜裂纹产生较少。由机理分析可知,翼型裂纹属于拉伸裂纹,以张拉应力为主;它会随着最大的主应力大方向发育扩展。此外,在进行对0˚倾角的裂隙单轴压缩时,观察到会先出现裂隙闭合的情况,之后出现裂纹生长和扩展以及应变软化。而相对于其他倾斜角度的裂隙模型,0˚倾斜裂隙模型更容易在压缩实验中产生裂隙闭合。
5. 结论
1) 对比图3中每个模型的单轴压缩实验的应力–应变曲线图,应力在达到峰值之前以及之后有着明显的波动性。同时随着应变率的上升,应力曲线波动出现由低幅向高幅转变。此外,裂隙倾角也影响着曲线波动,随着裂隙倾角的增加,峰值附近的曲线波动性有着明显的下降。
2) 有无裂隙对岩石的抗压强度有着一定的影响,预制裂隙的岩石的抗压强度均低于无裂隙的完整岩石试样,但是随着裂隙的倾角的增大,岩石的抗压强度有着明显的上升性,当裂隙倾角接近90˚时,岩石试样的抗压强度接近于无裂隙的完整岩石试样。
3) 岩石试样在进行单轴压缩时,所产生的裂纹数量跟抗压强度有着正相关性;随岩石的抗压强度的增加,单轴压缩所产生的裂纹数量以及岩石的应变率都会上升。
6. 工程应用
本文研究了不同倾角的裂隙对于岩石的抗压强度产生的影响以及不同倾角的裂隙产生裂纹扩展情况。基于实验的结果以及数据结论分析,在现实工程应用中,岩石工作者会经常遇到具有裂隙的岩石,当知道岩石内部具有天然的裂隙时,在施加外部应力的时候一定要注意应力的大小,尽量低于岩石的抗压强度。当外部的应力载荷超过岩石本身的抗压强度,岩石会产生破坏,而如果这块岩石处于一个应力集中区域,可能产生岩爆的现象,对人类的生命安全产生影响。随着学者对裂隙岩石的研究不断完善,岩土工程的事故也会逐渐减少,工作者的生命安全也可以得到安全保障。