1. 引言
由于地下水位变化、荷载释放、荷载增加、基础地质条件、基础处理方法等等因素的影响,建筑物在施工与运营期间会产生沉降,沉降量超过一定限度时会对建筑的安全性产生影响。考察建筑物沉降量分为两部分,一是绝对沉降量,它是建筑体上的监测点相对于周围的绝对固定点(通常认为埋设到基岩上的点才能作为绝对固定点)的沉降量;二是建筑物相对沉降,它是建筑体上监测点之间的相对沉降值(亦称不均匀沉降)。前者多用于研究建筑体所在区域的地质情况和验证某种理论,难点在于寻找固定基准点,而建筑物施工区域或附近很难找到这样的固定点;后者由于只考察建筑物施工与运行期间整体的不均匀沉降情况,因此其观测的基准点可以不用绝对固定点。
多年来,国内对变形监测的研究集中在变形监测基准点稳定性分析方面 [1] - [6] ,而无需布设基准点的沉降观测方案尚未见报道。
当施工与运营期间建筑体上的监测点出现整体下沉情况,但其相对沉降值很小或在规定的范围内,即使建筑物整体下沉量很大,也不会危及建筑物的安全。为此,若建筑物变形观测只是为了监测其施工与运营期间的安全性,就可以只考虑监测点的不均匀沉降量,即相对沉降量,这样就不用绞尽脑汁寻找固定基准点以及后续数据处理时的基准点稳定性分析、非稳定基准点剔除等繁琐的分析与计算工作。本文探讨无基准安全性沉降观测的方法和实践。
2. 沉降观测的基准与平差模型
沉降观测本身即是高程测量。高程测量数据处理时可以采用自由网平差,对应的基准有如下四种:
一是固定基准,即高程测量网中有绝对固定的基准点,对应的数据处理方法是经典平差;
二是重心基准,即将高程测量基准网整体的平均值作为基准,网中没有固定的基准,对应的数据处理方法是普通秩亏平差;
三是拟稳基准,即将高程测量基准网中一部分点作为基准,并采用这部分点的平均值最为基准,其余点作为非稳定点,对应的数据处理方法是拟稳秩亏平差;
四是加权重心基准,即将高程测量的基准点按稳定程度赋予一定的权值,其稳定权重在[0, 1]之间。0代表不稳定,1代表稳定(固定),其余点在(0, 1)间,其对应的数据处理方法是加权秩亏平差。
四种基准平差在最小二乘、最小范数条件约束下,可以用统一的数学模型 [7] [8] 来表达,即
(1)
(1)式中,第1式为误差方程,第2式为最小二乘条件,第3式为最小范数条件。GT为基准条件方程系数,Px为未知数的权,它代表点位的稳定程度。对式(1)求解得
未知数:
(2)
未知数协因数:
(3)
上述模型对于同一监测网,通过对px的取值不同,即可实现前述的各种平差。当知道网中一点绝对稳定时,取该点
,其余各点
,这时即为经典自由网平差;当网中各点无先验条件,即各点具有同等稳定程度时,取各点的px均等于1,这时平差结果即为普通秩亏自由网平差;当网中一部分点相对另一部分点稳定时,取相对稳定点组的
,其余点组
,平差结果即为拟稳秩亏自由网平差;当网中各点没有明显的稳定与非稳定界限,即各点均有一定的稳定性指标时,取
区间内的数值,其平差结果即为加权秩亏自由网平差。
由此可见,代表点位稳定程度的权px,在平差中起着重要的作用,它决定了平差基准,从而直接影响平差结果及点位位移量的计算。因此,在变形监测数据处理时,应根据项目的具体情况,合理确定px,从而选取适当的平差模型。px一般是难以合理确定的。
3. 绝对沉降量与安全性
若计算建筑物或监测区域的绝对沉降量,需要有1个或多个绝对不动的固定的基准点,每期观测均以这些基准点为起始,对监测体进行观测。分析剔除观测粗差后计算本期相对于初始周期的绝对沉降量或相对于某一期的相对沉降量。图1为有基准沉降观测网络示意图。

Figure 1. Sketch map of sedimentation observation with benchmark
图1. 有基准沉降观测网示意图
当基准点绝对固定不动情况下对建筑体上沉降测点进行多周期观测,得到观点测的下沉量即为绝对下沉量(△)。不管绝对下沉量(△)大小,若观测点各点间的相对下沉量在一定的允许范围,则建筑物是安全的,如图2中(1)所示。若观测点各点间的相对下沉量(d)超过允许范围,则建筑物无论绝对下沉量(△)多大,其可能存在安全隐患,如图2中(2)(3)所示。
由此看出,建筑物安全性沉降观测时,其安全性是由相对下沉量(d)决定的。因此,建筑物在进行安全性沉降观测时就不需要埋设绝对固定的基准点了。
4. 无基准点安全性沉降观测
无基准点包含两类:一类是无固定的基准点,但埋设相对固定的基准点(1个或多个),如图1所示。这种情况下当多周期观测时每隔一定的时间需要对基准点稳定性进行计算和分析,剔除非稳定的基准点,然后再用稳定的基准点重新计算观测点的沉降量。若存在非稳定的基准点,则给计算、分析造成非常大工作量,且成果即时性变得很差;第二类是绝对的无基准点观测与计算,如图3所示,每期观测计算监测体上点的相对沉降量,即不均匀沉降量,由此判别监测体是否安全。
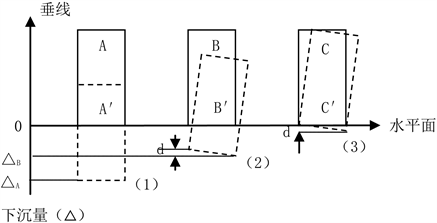
Figure 2. Sketch map of absolute and relative subsidence
图2. 绝对下沉量与相对下沉量示意图
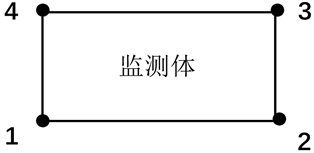
Figure 3. Sedimentation observation of no-benchmark
图3. 无基准沉降观测网示意图
绝对无基准观测,省去寻找、埋设(相对)稳定基准点的困难,观测网形简单,外业工作量小,计算简单。具体计算步骤为:
第一步,计算各点高程的改正数
。
公式(1),赋予
,即网点具有同样的稳定程度,采用重心基准平差(普通秩亏平差)。平差时以前一周期的各点高程值作为本次平差的初始值,计算各点高程的改正数
。由于采用重心基准平差,其
结果会有正(点位“升”)有负(点位“降”),即满足
(4)
第二步,计算本期相对沉降量
(5)
第三步,计算累计相对沉降量
(6)
5. 实验验证
沉降观测数据处理是件相对繁琐的工作,不同的基准条件采用不同的平差处理模型,且重复计算工作量大,为此沉降观测内外业数据处理一体化专家系统 [9] 将公式(1)中固定基准(经典平差)、重心基准(秩亏平差)、拟稳基准(拟稳平差)、加权重心基准(加权秩亏平差)等4类9种平差模型计算机系统化,便于沉降观测数据处理、数据分析与计算。本文计算采用该系统。
图4为南京某区域一建筑物施工期间的沉降观测实例。初始状态布设8个监测点,3个(相对)稳定基准点,共观测8期,其观测数据(摘录1、3、5、8期)如表1所列。基准点JZ1、JZ2在第2第三周期观测时即遭到了破坏,JZ3埋设在相对稳定马路上,持续保存。JZ3高程值为23.260 m。

Figure 4. Example of sedimentation observation
图4. 沉降观测实例布网图
假设JZ3为固定不动点,取该点的
,其余各观测点的
,(1)式按固定基准平差计算,得到各观测点的绝对沉降值如表2所列。
从表2分析可知,各点绝对沉降量均在9 mm左右,这一值是否绝对由于建筑体沉降所致,还是由于“固定点”不固定所致,要进行基准点稳定性监测与分析,要额外增加很多工作量。
表2中6号点的沉降值最小,以6号点为参考,计算各点的相对沉降值列于表2的最后一行。虽然说各点的绝对沉降值较大,但各点的相对沉降值最大相差0.45 mm (3点和6点),由此可见建筑物整体是安全的。

Table 2. Absolute settlement and relative settlement of fixed reference
表2. 具有固定基准的绝对沉降值与相对沉降值
注:表中△表示沉降量,单位为mm。
若将图4中的基准点全部剔除,即采用无基准点的安全性沉降观测,仍利用表1中的观测数据(剔除与基准点连接的测段),(1)式采用重心基准平差模型,即普通秩亏平差模型。观测网中无固定基准点,也无稳定点,即
。初期平差计算时可给观测点一初始高程值(如10.000 m),然后将初次平差计算后得到的高程平差值作为以后计算的初始高程值。每次平差后,以沉降值最小的点(或伪上升值最大的点)为参考点,按式(5)计算各点的沉降值与该点的沉降值作为本周期各点的相对沉降值,如表3所列。
表3最后一行与表2最后一行对应分析,其相对沉降值是完全一致的。因此,考察建筑物上监测点之间的相对沉降量,无需设定固定基准点。

Table 3. No-Benchmark relative settlement
表3. 无基准点相对沉降量
注:表中d表示相对初始周期沉降量,单位为mm。
6. 结论
建筑物在施工与运营期间的沉降观测,若观测是为了监测建筑物是否处于安全状态,考察其绝对下沉量要布设稳定的基准点,这给监测工作增加巨大的成本,一般是不需要的。若沉降观测只是为了监测建筑物的安全性,只要观测与计算观测点间的相对沉降量,由相对沉降量分析建筑物是否处于安全状态即可。这种安全性沉降观测无需布设基准点,将减少大量的外业成本。内业计算只采用重心基准平差就可以获得点位的相对沉降量。无基准建筑物安全性沉降观测将给沉降观测工作带来很大的便利性与作业成本。
NOTES
*第一作者。