1. 引言
数理统计思想起源于十九世纪以前的描述性统计,后来经过近代经典统计学和现代推断统计学的发展逐步发展为一门理论充实、应用广泛的学科 [1] [2] [3] [4] 。《数理统计》作为统计学学生的重要专业基础课及数学与应用数学专业学生的一门核心基础课对学生应用数学思想的培养起着举足轻重的作用。现如今,概率统计在各行各业开枝散叶,发挥着它的理论指导、数据发掘及统计决策作用,数理统计的思想方法越来越被各行业所接受 [5] [6] 。
随着国务院学位委员会、教育部联合印发的《国务院学位委员会、教育部关于设置“交叉学科”门类、“集成电路科学工程”和“国家安全学”一级学科的通知》出炉 [7] ,跨学科与交叉学科理念逐渐成为当前高等教育的热门话题与选择。基于此,在数理统计与数据处理高融合的前提下,计算机软件的仿真计算被大量的应用在本学科的教学中。本文以常用的仿真计算软件Matlab为载体,结合数理统计中的经典理论如抽样分布、统计推断、回归分析等内容进行模拟演示 [6] [8] ,使整个教学过程更加自然、和谐。Matlab的全称是“Matrix Laboratory”,译为矩阵实验室,在处理矩阵、向量等高维数据及高精度模拟、仿真等方面拥有强大的运算处理能力 [9] 。
基于仿真计算在各行各业中大量的应用及带来的便利,作为应用性很强的《数理统计》课程也必然会从仿真计算的应用中获益。固然课程中的概率思想及数学分析理论推导过程是必不可少的,但也不可避免会带来知识的固化与学习者的困惑:我们需要这些理论知识,但我们也需要更加生动直观的呈现出来。经过作者多年的教学实践,作为一款功能强大的科学计算与仿真软件,Matlab在数理统计的教学过程中可以方便的呈现这些问题,并通过多年的教学比对发现学生在大量应用仿真软件后比以前能更好的消化、理解经典的数理统计思想,对重要知识点的认识有了很大的改变,对学习也产生了更加浓厚的兴趣,取得了更好的学习效果。
2. 仿真计算在抽样分析中的应用
经典的数理统计教材中基于各种原因很少出现仿真软件的结合,然而实践下来却发现,适当的仿真软件的应用必不可少。众所周知,数理统计教材附表中的分位数表,提供了标准正态分布、学生氏分布、卡方分布、Fisher分布、W检验等分位数表,但无一例外这些分位数表也只能在有限的篇幅中选用一些特殊的
值,如
等,显然这样的设计限制了抽样概率、置信区间或显著性检验中的概率的应用,使得问题变得不易处理。下面通过几个例子来对此问题进行阐释与解决。
案例1 [2] :在“正态总体抽样分布”这一环节的学习过程中,经常会遇到研究某统计量取值区间的概率计算问题。这类问题比较常见的是基于易查分位数的概率计算,如
,这是很简单的计算,因为基于
的查表事实。但是分位数表总归是有限的,离散的,并不能提供统计量在每一个区间中的概率计算。
比如从总体
中抽取容量为20的样本
,求概率
,则转化为
,显然20与10这两个分位数无法查表,考虑到卡方分布的连续性,可以进行一次线性插值做近似计算,这种方法除了近似度不高以外,计算的复杂度也较大,此时可以应用Matlab语言,
>>chi2cdf(20,20)-chi2cdf(10,20)Ans=0.5102
也即顺利得到:
,类似也可以参考下面案例2。
案例2 [2] :从
中抽取容量为16的样本
,样本方差
,求样本均值与总体均值的距离在0.1至0.5之间的概率,即求概率
,则转化为
。
Matlab语言为:
>>tcdf(4,15)-tcdf(0.8,15)
Ans=0.2175
从而有:
。
3. 仿真计算在随机模拟与分布拟合中的应用
问题1:计算机随机模拟以显示不同的参数取值对分布密度曲线的影响
在五大抽样分布“伽马分布、贝塔分布、卡方分布、学生氏分布、F分布”的内容学习中,经典的教材会通过数学分析的推导过程,如通过微分的方法运用一阶、二阶导数讨论密度函数的单调性、峰值点(众数)、凹凸性等常见的函数性质,这些分析方法从知识系统的严谨性上当然是不可少的(当然要耗费大量的课时,可以根据各校课时情况有选择的在课堂中加以体现),但是真实的分布形态是否正如理论推导的那样呈现这种规律性呢?Matlab仿真软件提供了通过产生随机数来画出概率密度函数的方法,作为知识体系的有益补充,可以拿来所用。
案例3:通过Matlab仿真探讨伽马分布Gamma(α, λ) [3] 的密度函数图像随着形状参数α改变而改变的规律。
(分别取
,
)
Matlab语言为:
>>x=0:0.01:8; y1=gampdf(x,1,0.6);y2=gampdf(x,2,0.6);y3=gampdf(x,4,0.6);
>>plot(x,y1,'.b',x,y2,'.g',x,y3,'.k');
>>title('Gamma分布不同形参的密度函数图像');
>>legend('Gamma(1,0.6)','Gamma(2,0.6)','Gamma(4,0.6)');
[分析]图像如图1所示,从实验仿真的角度验证了:当
时f递减(
即为指数分布);当
时,f先上凸后下凸;当
时,f先下凸再上凸后下凸。由于
即为
分布,从而当自由度n > 4时,即与
时伽玛分布的图像类似。

Figure 1. Density function of Gamma
图1. Gamma分布密度函数曲线
案例4:Beta(a, b) [3] 的密度函数图像随着参数a,b的改变而改变的规律(分别取a = b = 0.5;a = 2,b = 3;a = 0.5,b = 2;a = 2,b = 0.5;a = 1,b = 2;a = 2,b = 1)。
Matlab语言为:
>>x=0:0.001:1;y1=betapdf(x,0.5,0.5);y2=betapdf(x,2,3);y3=betapdf(x,0.5,2);y4=betapdf(x,2,0.5);y5=betapdf(x,1,2);y1=betapdf(x,2,1)
>> plot(x,y1,'.b',x,y2,'.g');legend('Beta(0.5,0.5) a<1 b<1','Beta(2,3) a>1 b>1');
>> title('Beta分布不同形参的密度函数图像a<1 b<1 VS a>1 b>1');ylim([0 10]);
[分析]可得Beta(0.5, 0.5)与Beta(2, 3)的密度函数在同一个坐标系中的图像如图2所示,一定程度上也反映了当参数a < 1,b < 1时贝塔分布的图像与a > 1,b > 1时贝塔分布的图像成上下对偶排列。类似也可得当参数a < 1,b > 1时贝塔分布的图像与a > 1,b < 1时贝塔分布的图像成上下对偶排列(图3);当参数a = 1,b > 1时贝塔分布的图像与a > 1,b = 1时贝塔分布的图像成上下对偶排列(图4)。
案例5:
[1] [2] [3] 分布的密度函数图像随着双自由度的改变而改变(分别取m = 10,n = 5;m = 10,n = 25)。
Matlab语言为:
>>x=0:0.001:12; y1=fpdf(x,10,5);y2=fpdf(x,10,25);
>>plot(x,y1,’.r’,x,y2,’.b’); legend(‘F(10,5)’,’F(10,25)’);title(‘F分布双自由度对密度函数的影响’)
图像如图5所示。随着第二自由度的增大,图像呈现更高的峰及更细的尾部。

Figure 2. Density function curve of Beta
图2. Beta分布密度函数曲线
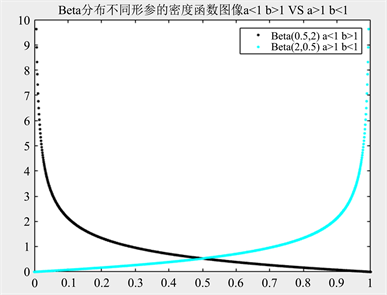
Figure 3. Density function curve of Beta
图3. Beta分布密度函数曲线
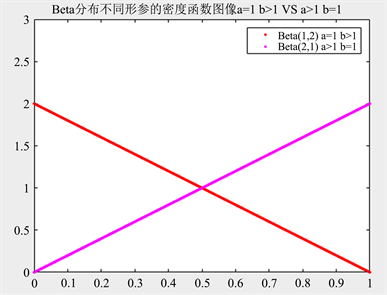
Figure 4. Density function curve of Beta
图4. Beta分布密度函数曲线
案例6:
分布的密度函数随方差
的变化而呈尖峰值或厚尾性(分别取σ = 1,σ = 5,σ = 10,μ = 3)。
Matlab语言为:
>>x=-20:0.01:20;y1=normpdf(x,3,1);y2=normpdf(x,3,25);y3=normpdf(x,3,100);
>>plot(x,y1,’.r’,x,y2,’.b’,x,y3,’.k’);legend(‘N(3,1)’,’N(3,25)’,’N(3,100)’);ylim([0 0.6]);
>>title(‘正态分布图像受不同方差的影响效果’)
[分析]图像如图6所示。从中不难发现,σ越小,正态取值越集中于μ附近,图像的峰越尖,尾部越细;反之,σ越大,正态取值越分散于μ的两边,图像的峰越缓,尾部越厚,也即发生异常值的概率越大,在金融风险中预示着投资的风险越大,但获得超高收益或超低收益的概率也越大。
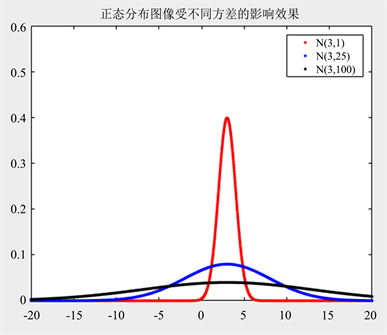
Figure 6. Influence of different variance to N
图6. 不同方差对正态分布的影响
问题2:对已有样本数据的适当分布拟合
大多数数学系或概率统计系所授《数理统计》课程中,最核心的知识内容就是统计推断,也就是根据已有的样本数据,基于参数估计、假设检验、分布拟合等方法对数据进行加工处理与信息挖掘,以期发现一定的统计规律,为以后的工作生活提供适当的决策指导。比如对教师工作来说,教学方法是否科学,学生接受程度是否理想,试卷题目内容及分值分配是否科学合理等,其实通过考试成绩这个样本数据可以一定程度上反映出来。
案例7:试对某学期某班的《数理统计》课程的期末考试成绩做分布拟合。
>>x=[78 84 81 97 71 80 68 …84]; 共64个样本数据
>>normplot(x);histfit(x);[skewness(x) kurtosis(x)]; [mean(x) median(x) std(x)];
[分析]正态QQ图7显示分数数据基本服从正态分布;直方图拟合图8也显示数据与正态钟形曲线初步拟合;K-S非参检验(SPSS结果图9)显示p-value = 0.760 > 0.05,定性分析考试分数服从正态分布。偏度Skewness = −0.6013 (轻微左偏),峰度kurtosis = 3.1684 ≈ 3 = 正态分布的峰度,
,即平均分79.8281,中位分数80.500,标准差12.089。可认为本次考试成绩服从正态分布
。从中可以得到79.8分的卷面均分及12分的标准差说明学生基本可以掌握80%的学习内容,且标准差在15分以下,同学之间的差距并没有太大,也反映了在本学期本门课程的学习中,大多数同学能跟得上教师的教学进度与难度,且成绩拥有较好的正态性。
4. 仿真计算在经典统计推断中的应用
统计推断主要有参数估计、假设检验(含分布拟合检验)等内容,一直以来都是学习数理统计的重点及难点。传统的课堂学习注重理论传授与统计思想的点播,如在矩法估计中会介绍Pearson的替换原则,MLE中会介绍高斯和Fisher的似然函数思想,区间估计中会围绕枢轴量展开学习,假设检验中会引入实际推断原理(概率意义下的反证法)等等。这些都是优秀的理论思想,如何将这些好的理论更好地呈现在课堂上,高效的仿真计算软件就非常有用了。
案例8:通过构造两个正态随机向量,并比较它们的均值是否相等?并给出总体均值之差的95%置信区间(分别产生两个100维的
及
随机向量,做假设检验
,并给出
的95%置信区间) [9] 。
Matlab语言为:
>>x=normrnd(0,2,100,1);y=normrnd(0.5,2,100,1);[h,sig,ci]=ttest2(x,y); z=[x,y]; boxplot(z)
>> plot(sort(x),normpdf(sort(x)),'+r',sort(y),normpdf(sort(y)),'.k')
[分析] h = 0 (接受原假设);p-value = 0.7245 > 0.05不显著,不拒绝原假设;
的95%置信区间为[−0.7145, 0.4976]含有0点,故不拒绝
的原假设。箱线图如图10所示,显示两总体均值无显著区别。两随机向量的密度函数图如图11所示,两组数据的正态值基本同步拟合,且正态性较好。
案例9:对12名女子的身高(x: cm)与腿长(y: cm)数据:

Table 1. Sample data of height and leg length
表1. 身高与腿长的样本数据
试结合表1的样本数据对身高与腿长变量做一元线性回归分析。
① 散点图
>>x=[149 150 153 154 155 156 157 158 159 160 162 164]’;y=[92 93 93 95 96 98 97 96 98 99 100 102]’;plot(x,y,’.r’) ;corr(x,y)
② 建立回归模型
>>x=[ones(12,1) x];
>>[b,bint,r,rint,stats]=regress(y,x) ;[mean(r) var(r)]
[分析]散点图12表明身高与腿长具有明显的线性关系,相关系数r = 0.9587强相关;回归直线方程为
,回归直线与散点图的同框如图13所示;线性模型
中,参数
与
的95%置信区间分别为[−24.3257, 17.4767]与[0.5058, 0.7729];每个观测点与回归方程的残差结果分别为0.1586,0.5193,−1.3988,−0.0382,0.3224,1.6831,0.0437,−1.5957,−0.2350,0.1256,−0.1531,0.5681;
的结果表明回归的
,模型检验的F-value = 113.7486,检验的p-value = 0模型高度显著;误差方差
;而对残差序列r来说
,
,r的的正态Q-Q图如图14所示,残差序列的K-S正态性检验如图15所示,p-value = 0.573,接受故残差为正态分布,从而线性回归模型拟合为:
基于这个线性回归模型则可以对成年女性身高与腿长的大致关系进行计算,如身高170 cm的女性,其腿长大约为−3.4245 + 0.6394 × 170 = 105.27 cm。
5. 仿真计算引入课堂后的课程计划建议
以笔者所在院系《数理统计》课程48学时的情况来看,正常的知识理论讲授及习题训练可以安排40学时,教师仿真计算案例演示可以占用4学时(因为是课堂穿插,所以是估计),学生上机实验4学时,当然这4学时也可以以课后家庭作业的形式进行,毕竟在总学时数不宽裕的情况下,每一学时都是宝贵的。如果有软件类或科学计算类课程设置的话,完全可以在此课程中加入“数理统计”或“统计推断”模块,辅以科学的考核方式,会达到更好的学习效果。当然所有这些呈现都需要学校平台基本的资源配备,如多媒体教室、学生机房、正版软件等加持,相信所有这些随着国家对教育投资的加大及不同院校校内资源的合理规划是可以实现的。
6. 总结
本文阐述了仿真计算在数理统计中经典的抽样分析、随机模拟、统计推断(区间估计、假设检验、回归分析)中的应用方法。作为数学专业的同学来说,掌握扎实的理论基础固然重要,结合各种数学软件熟练的处理各种实际问题也必不可少。文章选用了Matlab仿真计算软件作为载体,当然老师们可以根据自己的习惯选用适合自己的、学生易于接受的仿真软件进行辅助教学工作。比如在《多元统计分析》中常用SPSS或SAS统计软件做分类分析(聚类分析与判别分析)、降维分析(主成分分析与因子分析),在《时间序列分析》中常结合Eviews软件做线性时间序列B-J模型和异方差ARCH类模型等。适当的模拟仿真及科学计算对数理统计等应用类学科的学习可以起到画龙点睛的作用,也可以在学习过程中起到润滑的作用,帮助学习者提高学习兴趣以及更灵活的进行数据处理。
感谢文中所有参考文献作者所做的卓越工作。
基金项目
上海理工大学教师发展研究项目(CFTD2023YB40)。
NOTES
*通讯作者。