1. 引言
分类被划分为单一分类的方法还有用于组合单一分类法的集成学习算法,其中单一分类法就包含了好几种,其中我们经常使用和借鉴的就有支持向量机、贝叶斯分类法等,组合单一分类法就包含了Boosting等方法。其中,贝叶斯分类应用更加广泛,经常应用于文本分类等问题当中,相比于其他算法来说,其模型也相对简单,除此之外贝叶斯分类算法所消耗的时间和空间的占用也相对较小,但每一个方法都不是完美无暇的,本文旨于优化贝叶斯分类算法,使其分类的错误率被降低,减少应用场景的限制。
随着我国经济的快速发展,信息化的趋势越来越明显,数据化的发展速度也越来越快,相应地,分类算法的优化需求也越来越大。伴随着这些方面的加速前进,各种新形式且传播速度非常快的传播手段也应运而生,应时代而生。本论文主要研究贝叶斯分类算法,应用于文本及信息的分类方面。首先,为了克服贝叶斯分类的属性独立性的假设,而进行了基于主成分分析的加权贝叶斯分类。其次,提出了一个专门应用于将网络信息分类的贝叶斯分类算法,即基于互信息特征选择的贝叶斯分类优化法。
2. 贝叶斯分类的研究现状
在对优化贝叶斯分类算法过程中,有很多研究成果值得我们参考学习和借鉴,邓桂骞等 [1] 先通过属性重要性公式对将要进行数值实验的数据进行简约化的处理,删除了部分属性以及相关的数值,再通过文中提供的权值公式赋予数据中条件属性不同的权值,后通过计算可知其后验概率,通过数值实验提出了OBCA (Optimal Bayes Classification Algorithm)算法。同样是从削弱条件独立性假设方面思考入手,为了能让贝叶斯分类能更多的应用在实际数据挖掘中。张明卫等 [2] 在中也提出了一种先计算数据中哪个是决策属性哪个是冗余属性,再通过将相关系数不同的属性赋予不同的权值,并且通过研究算法的原理和计算求得条件属性和决策属性之间不同的相关系数,对不同的属性赋予不同的权重,虽然计算量有所增加,但却减少了无用数值和属性的干扰,在实验数据简单性提升的基础上,使朴素贝叶斯算法的分类性能被有效地提高。陈景年 [3] 通过分析以往对贝叶斯分类器的优化,找到一个自己的优化方法,就是选择性贝叶斯分类,他发现在以往的贝叶斯分类过程中对不完整数据的分类效果也有着不错的表现,因此在一个大量的数据集中选取一小部分也就是不完整的数据进行贝叶斯分类,并且通过实验这种基于不完整数据的分类算法有了新的名字,它被命名为DBCI (Distribution-based Bayesian Classifiers for Incomplete data)。即使在这些选取的有缺失的数据中也可能会包含着大量影响分类结论和有用的多余属性或毫无作用的属性,但在这篇文章中作者也使用包装法给出了两个对选择性不完整数据有着良好性能的分类器。在文章的后半部分,作者特意针对在实际分类应用中贝叶斯分类应用频率最多的高维数据——文本数据,而提供了两个用于当贝叶斯分类器被用于高维的文本分类时可以使用的评价函数,通过在文本数据集上的分类正确率的结果显示,利用这两个属性评价函数构造的选择性贝叶斯分类器具有更好的分类效果。吕昊等 [4] 在2012年发表的《改进朴素贝叶斯分类算法的研究与应用》一文中通过优化参数的方法,提出了一种通过增强实际例子中特征的学习方法,从而得到了一个高准确度且耗时较短的分类算法,并将此方法应用到了油水层识别问题中,有着令人满意的实验结果。在2011年计算机工程与应用上发表的论文中,张亚萍等 [5] 提出了与陈景年思考角度相反但同样都是针对朴素贝叶斯分类算法改进的问题,并应用于高校教授等级的评定中,前者是考虑将缺失数据填补完整的问题,针对这一个“补数”的问题,他们提出一种基于EM (Expectation Maximization)算法的朴素贝叶斯分类算法,根据读阅论文可知该算法首先根据已有数据的属性相关程度对缺失的数据有了一个大概的范围,并将估计值作为输入到EM算法中最一开始的值,直到迭代计算到E步M步后才完成了数据的填补,然后用贝叶斯分类算法进行分类,通过这次对数据补齐的实验说明,改进的贝叶斯算法具有较高的分类准确度。王晶 [6] 等在单关系学习中分别重点介绍了几种基于粗糙集的加权贝叶斯分类算法,分析了这几种方法中所包含的模型的建立、流程及优缺点,用了较少的篇幅介绍多关系学习中的语义关系图以及和贝叶斯分类算法结合后的效果,并在文中重点介绍了MRNBC (Multi-relational Nave Bayesian Classifier)模型。Weibin等 [7] 从加权朴素贝叶斯方面入手提出了一种对朴素贝叶斯算法的改进和扩展的方法,论文中的方法分别是从数学理论、信息观的角度出发给出了求解属性权值的办法,再通过常用的数据网站寻找到了真实的数据集并进行实验,并在此篇论文中验证了该方法的可靠性。在《不同类变量下属性聚类的朴素贝叶斯分类算法》中彭兴媛、刘琼荪 [8] 通过多次数值实验完成了他们最初提出的想法:去除条件独立性假设对分类效果的影响,在实验的过程中他们甚至还提出一种新的分组技术,那就是将之前的条件属性进行聚类处理,通过聚类处理后的数据,既在一定程度上避免了各条件属性间独立性对分类结果造成的影响,又可以反映出不同类别情况下属性关联程度的大小。丁钢坚,张小刚 [9] 在《贝叶斯分类算法应用于回转窑烧结温度预测模型》一文中的主要目的是将贝叶斯分类算法作为一种实现途径从而建立一种用于预测回转窑烧结温度的模型,本文采用了FastICA (Fast Independent Component Correlation Algorithm)算法,为了满足贝叶斯分类算法属性之间相互独立的前提条件,作者先在预处理完之后的数据中找出独立成分,再通过AdaBoost算法对模型进行改进和提升,通过文中最后的实验成果可以看出,这种模型对回转窑烧结温度的预测具有较好的效果。张留决 [10] 在“计算机时代”上发表的文中提出了一种基于密度函数的高斯朴素贝叶斯分类算法,且论文中数值实验针对的是连续性数据,这种算法的前提与贝叶斯算法的前提类似,在进入分类器之前需要假设各特征值都符合正态分布,并计算出计算密度函数所需要的方差和均值,在做好以上两个准备工作后再计算各特征值的概率密度函数,最后利用高斯朴素贝叶斯分类器得到预测结果。作者又将改进后的方法在某单位的分类问题上进行应用,通过应用不难发现改进后的分类结果较改进之前在功能和准确性方面都有很大程度的提升,这说明这个算法具有可行性。
3. 基于主成分分析的加权贝叶斯分类
3.1. 主成分分析的过程
主成分分析是一个归属于统计的方法,也是我们在处理数据时常用的降低数据维数的方法,下面通过一个数值实验实现主成分分析,为后面与贝叶斯结合对属性加权做好准备。这是一个拥有11个变量的数据集,此次实验的目的是为了让数据简单化,找出11个变量中的主成分,并判断工人的技术评级与上级的私交有没有关系。首先,将要保证数据的完整度,再开始实验,先做一个碎石图,通过碎石图可以判断出在11个变量中有几个主成分,碎石图结果如图1。
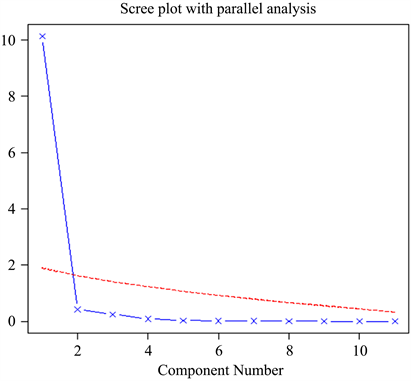
Figure 1. Principal component lithotripsy diagram
图1. 主成分碎石图
由图1可读取到在数据集11个中需要提取一个主成分,因为11个变量中仅有一个变量的特征值较大,明显大于1。下面就要找出这个变量到底是哪一个,在这一步中,需要求参并旋转关系矩阵,最终求出得分,如图2。
在获取各变量的得分后,需要获取上文变量中主成分变量的得分情况,在求求出其相关系数,便可得出结论,如图3。
由图3可以得出结论,工人的技术评级与上级的私交没有关系。至此,数值实验中主成分分析过程已经完整的实现。
3.2. 加权属性的贝叶斯分类
在朴素贝叶斯分类中,最显著的特点就是令数据集中所有的属性,不论对决策影响大还是小,占比相同,权重均为1。但在实际的学习中,所有特征对决策影响相同的情况是很难出现的。因此,有很多人提出并完成了基于贝叶斯分类,将涉及的所有属性进行加权,实现对贝叶斯分类的优化,在保证原有贝叶斯分类器可靠度的基础上对分类器进行进一步优化完善。
在此次数值实验中,先将数据进行预处理,保证所作实验中数据的完整度,再放入基础的贝叶斯分器中进行分类以提供一组对照,方便加权前后分类效果的直观比较。再按照上一个小节中的步骤将数据进行主成分分析,找出主成分变量个数和占比,进行简单的加权处理,求出权值,最后带入贝叶斯分类器中,得出分类结果及概率,多找几个数据集重复上述步骤,反复检测这种方法的可靠度,以免碰巧事件的发生,将分类的结果对照情况做一个汇总,如表1。

Table 1. Comparison table of weighted naive bayes classifier results
表1. 加权朴素贝叶斯分类器结果对照表
由表1可看出,加权后的分类器较加权前的分类器准确率有所提高,但此次数值实验中的数量都较小,而且组成比较简单,因此此方法不一定可以适用于大多数情况。
4. 基于互信息特征选择的贝叶斯分类
4.1. 互信息的基本原理
互信息是一个属于概率论和信息论两方面理论的概念,衡量的是数据集中两个或者几个变量间的相互依赖程度,当数据集中的两个变量是离散或连续时,互信息的定义相同,但计算是稍有不同,其中离散定义式如(1)式。
(1)
当两个变量是连续的时候,(4.1)式中的求和就会被二重积分取代计算,如(2)式。
(2)
由(1)式和(2)式可知,只有当X和Y这两个变量独立分布的时候,互信息的值才会等于0,因此,互信息的性质中包含是有非负性的。除了非负性,在求值时
与
的值相等也就是说互信息还具有对称性。在日常的学习和应用中也能经常看到对互信息的应用,尤其是在通信和处理数据分类像在k-均值分类中被用作优化手段。
4.2. 改进算法应用
在本小节中,将互信息和贝叶斯分类相结合,并应用于文本分类的具体实例中,组成一次完整的数值实验。首先,从新闻中随机截取2类,各5个片段进行实验,通过互信息进行文章中的特征选择,再根据所选的特征求出与不同类别的概率,理论上将特征词与哪个类别的概率大,就跟这个类别的相关性强,最终就被划分到最强的一个类别中。在此次实验中,分别进行去除互信息中关联性强的10个词和随机去除10个词进入贝叶斯分类器分类的实验,在最后对比实验前后分类的正确率。此实验一开始需要将每篇文章中像“的”等高频虚词进行去除之后,再进行文章中高频词的统计,找出高频特征词后再进行与类别的互信息计算作为先验概率,计算的公式为(3)式,求出的数值越大说明这个特征与所计算的文本类同时出现的可能性越大。
(3)
在找的两类,共十篇的文章中进行三个特征词数量的统计,并绘制到表2中,后利用定义进行每个特征词与类别文本互信息的计算,计算出的数据分别是−0.221、0.001和−0.096。

Table 2. Statistical table of characteristic words
表2. 特征词统计表
在python中实现计算MI的值,并对互信息特征选择对文本分类试验前后的准确率进行统计和比较,可得使用互信息贝叶斯文本分类的准确率是0.925,而随机选择新闻中的特征进行分类的准确率仅为0.615。由此可得,在小容量的文本分类别的实验中,通过互信息进行文本分类的准确率能明显提升。
5. 总结
虽然这是一个比较简单且应用广泛的分类器,但是在实际应用中也是多变的,在很多情况下是有一部分局限性的。本文分别对已经提出的加权属性贝叶斯分类与主成分分析进行结合,又对互信息特征选择的贝叶斯分类器进行实现与应用。在基于主成分分析的加权属性贝叶斯分类中,削弱了贝叶斯分类先验概率条件独立假设的问题。通过五个不同数据集加权前后分类效果的比较,可以看出改进后的朴素贝叶斯分类具有比改进前更可靠的分类结果。在对互信息特征选择的贝叶斯分类器中,进行了两类,10个小新闻的分类,也有较好的分类结果。说明这两种改进方法,对于小容量的数量集的分类有着较好的效果。