1. 引言
横向稳定杆作为汽车悬架系统的一种特殊的弹性元件,可以有效地增加悬架的侧倾刚度,从而减小汽车转向时车身的侧倾倾向,还可以恰当地分配前、后悬架的侧倾角刚度比值,有助于汽车获得所需要的转向不足特性。目前对于复合材料稳定杆的研究很少,Kim [1] 使用第三代碳纤维增强塑料制造方法提高生产率,通过有限元分析确定复合材料稳定杆的几何参数,最终通过过程能力分析了制造方法的可行性。国内外目前对稳定杆的研究主要集中在优化设计与主动控制研究方面。伍文 [2] 提出一种新型长度可变、刚度可调节的非线性横向稳定杆,采用遗传算法对汽车性能进行优化。李能辉 [3] 对对汽车横向稳定杆的轻量化参数优化设计,评估不同参数汽车对横向稳定杆轻量化的影响,并获得最佳的结构参数。方辉 [4] 构建并改进汽车整体动力学模型,以悬架垂向刚度为基准对其灵敏度进行优化。潘海 [5] 对稳定杆在载荷作用下的位移和扭转刚度进行了研究,发现结构存在一些局部应力过大的问题,提出了结构优化方案,减小局部应力问题。Zhang [6] 基于某款轿车进行参数化设计和有限元分析,并对稳定杆的结构强度和刚度进行了定性分析。Kon [7] 提出了一种新的车辆液压主动稳定杆系统的主动侧倾控制算法,通过算法和仿真平台验证所提出的控制算法改善了车辆横摆动力学响应。
轻量化是实现节能减排和解决电动汽车续航历程不足的重要途径。实现手段包括:轻质材料替代、结构优化和先进制造及装配工艺应用。其中,轻质材料替代的轻量化效果最为显著。目前汽车悬架系统中板簧与螺旋弹簧等弹性元件在复合材料领域已经广泛使用。Ke [8] 引入材料制造复合材料板簧能使得在不降低承载能力甚至提升整车性能的情况下实现轻量化成为可能。相比同功能的金属螺旋弹簧,采用纤维增强树脂基复合材料制作的螺栓弹簧不仅能减重40%以上,而且具有断裂安全性,其缓冲减震能力和疲劳寿命理论上也明显高于金属螺旋弹 [9] [10] [11] 。
综上所述,目前汽车稳定杆集中在参数化优化与主动控制方面,而且由于复合材料的各向异性及其复杂性,人们对复合材料横向稳定杆的了解仍十分有限,这在一定程度上阻碍了它的推广。本文中首先针对复合材料横向稳定杆在众多轻量化材料中进行了选材,然后基于层合板理论和各向同性稳定杆理论建立复合材料稳定杆刚度模型,最后通过有限元分析的方法对复合材料稳定杆的刚度强度性能进行模拟,并对稳定杆模态进行分析,验证了复合材料稳定杆的可靠性。同时将理论计算结果与仿真结果进行对比,误差在允许范围内,验证了复合材料稳定杆刚度理论的正确性。
2. 稳定杆选材及刚度理论
2.1. 复合材料稳定杆选材
在众多的轻量化材料中,玻璃纤维复合材料具有优异的性能:机械性能强,材料的拉伸强度低于钢,高于球墨铸铁和混泥土,而比强度大约是钢的3倍,球墨铸铁的10倍;耐腐蚀性能好,可以通过合理的原材料选型和科学的厚度设计,玻璃纤维复合材料在酸、碱、盐等有机溶剂环境中可长期使用;相对碳纤维复合材料,价格只有其二十分之一。综合性能和材料成本,本文中的横向稳定杆选用玻璃纤维复合材料。
2.2. 金属刚度理论
为计算金属稳定杆刚度将稳定杆简化为图1所示,对应具体的材料参数与结构尺寸如表1所示。稳定杆在力F作用下发生弹性变形,根据能量守恒定理,F作的功与稳定杆中总的变形位能相等。
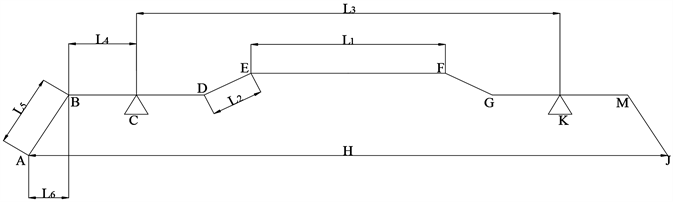
Figure 1. Stabilizer bar structure dimension parameter diagram
图1. 稳定杆结构尺寸参数

Table 1. Stabilizer rod structure dimensions
表1. 稳定杆结构尺寸
其中稳定杆的变形位能计算如下:
(1) BM段的扭转位能。
(1)
式中:J为稳定杆的截面惯性矩;G为材料剪切弹性模量;L1为EF段直线长度。
(2) AB段的弯曲位能。
(2)
(3) CK段的弯曲位能。
(3)
(4) BC段的弯曲位能。
(4)
F所作的功与稳定杆的变形位能相等,则
(5)
得
(6)
由于BC段一般很小。可以忽略右式第四项,得
则金属稳定杆刚度为
(7)
其中:E为材料弹性模量,
;J稳定杆的截面惯性矩,
;d为稳定杆的直径;F
为端点作用力;f为端点的垂直位移。
2.3. 复合材料稳定杆刚度
对于复合材料稳定杆受载荷时发生扭转,稳定杆扭转剪切模量的理论分析与纤维复合材料平板剪切模量分析是一致的,均与纤维含量和纤维方向有关。
单向纤维层合板的横向弹性模量ET [12] 的计算式为
(8)
式中:Em为试样基体的弹性模量,Vf为纤维体积分数。
对于单向纤维层合板的纵向弹性模量EL可用混合律公式进行计算
(9)
式中:Ef为试样基体的弹性模量,Vm为基体体积分数,它与Vf之和恒为1。
当正交织物编制角度与轴线成
时,复合材料平板的剪切模量为
(10)
式中:G12为0˚的面内剪切模量;E1为纤维方向的弹性模量;E2为垂直纤维方向的弹性模量;
、
分别为相应的泊松比。对于
对称正交纤维复合材料铺层平板,则有
,
。
对于正交铺层复合材料平板,在±45˚两方向弹性模量都表示为
(11)
式中VL、VT分别为纵向与横向铺层的体积含量,此处均为1/2。
将弹性模量与剪切模量带入公式7中得到,当正交织物铺层角度为
时,可得复合材料横向稳定杆刚度为
(12)
对于正交织物按±45˚铺设得到的复合材料稳定杆,其刚度为:
从上式中可以看出,复合材料稳定杆的刚度与两类参数有关,一类是与制成稳定杆的复合材料有关的参数(如Ef、Em、Vf、Vm);另一类是稳定杆自身结构特征尺寸参数(L3、L4、L5、D)。表明这两类参数共同影响着复合材料稳定杆刚度。
2.4. 稳定杆关键参数灵敏度分析
由公式12可知,稳定杆的刚度性能取决于材料设计与稳定杆自身结构特征尺寸。其中材料设计主要由弹性模量E决定,稳定杆自身结构特征尺寸受自身的截面惯性矩影响较大,而惯性矩由稳定杆外径D决定,因此通过对这两个稳定杆刚度的关键参数进行灵敏度分析。
由图2所示,稳定杆刚度与材料的弹性模量E成线性正相关,刚度变化系数为定值k,稳定杆刚度与其外径尺寸D成非线性正相关,随着稳定杆的外径逐渐增加,刚度的变化幅度明显增加。因此,相对于弹性模量E,稳定杆刚度对其外径尺寸D敏感度更高。
 (a)
(a)  (b)
(b)
Figure 2. Relationship between stiffness and key parameters: (a) Influence diagram of outside diameter; (b) Influence diagram of elastic modulus
图2. 刚度与关键参数关系图:(a) 外径影响图;(b) 弹性模量影响图
3. 有限元分析
3.1. 有限元模型建立
本文选取某轿车稳定杆为分析对象,采用三维建模软件(Solidworks)分别建立金属稳定杆和玻璃纤维复合材料稳定杆的三维数模,模型由稳定杆与橡胶衬套构成。金属稳定杆为实心结构,直径为22 mm,玻璃纤维考虑工艺问题设计为空心结构,内径6 mm,外径28 mm,如图3所示。
 (a)
(a) (b)
(b)
Figure 3. Three-dimensional model of stabilizer bar: (a) Metal stabilizer bar model; (b) Composite stabilizer bar model
图3. 稳定杆三维模型:(a) 金属稳定杆模型;(b) 复合材料稳定杆模型
根据建立的稳定杆三维模型,计算得到金属稳定杆和复合材料稳定杆的质量如表2所示。
3.2. 模型材料设置
金属稳定杆一般选用材料为60Si2Mn,屈服强度为1391 Mpa,杨氏弹性模量
,泊松比
。
玻璃纤维复合材料的工程常数如表3所示。

Table 3. Glass fiber composite engineering constant
表3. 玻璃纤维复合材料工程常数
稳定杆橡胶衬套采用的实心橡胶,可以承受较大的应变,具有明显的非线性特征。一般假设橡胶材料是各向同性且不可压缩的超弹性材料,主要通过应变势能描述材料的本构模型,本文中采用Mooney-Rivlin应变能模型作为橡胶材料本构,具体的材料参数如表4所示。
3.3. 铺层设计
复合材料构件的性能于铺层角度有关,合理的设计铺层角对于构件的性能有很大的提升。目前对于复合材料的铺层角度集中在0˚、±45˚与90˚,单一的0˚与90˚对于构件的拉伸强度性能有较大的提升,±45˚复合材料更能满足构件整体的拉伸、弯曲、扭转性能。汽车行驶在路面时稳定杆两端主要承受扭矩,对扭转性能、弯曲性能要求更高,因此本文中玻璃纤维复合材料稳定杆采用±45˚的铺层角度设计,具体如图4所示。在三维坐标系中,1代表纵向,2代表横向,S代表铺层堆叠方向,红色实线代表了纤维方向。
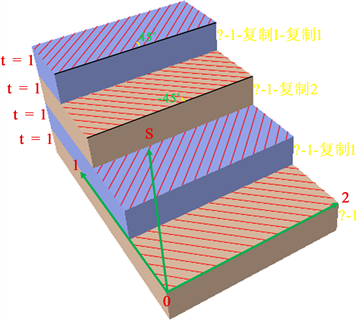
Figure 4. Composite material apply effect diagram
图4. 复合材料铺层效果图
3.4. 网格划分
网格质量直接影响计算结果的准确性,因此本次有限元模拟中采用C3D8六面体网格,并且为了保证有限元计算能够顺利运行,对局部弯曲部分进行加密种子提高网格密度,如图5所示。
3.5. 边界条件与载荷设置
稳定杆两端分别设置参考点RP-1、RP-2,并分别将参考点与所在截面进行耦合设置,以便于设置边界条件。橡胶衬套用于限制稳定杆中间杆运动时的自由度,同时对稳定杆起到支撑与保护作用,因此需要对橡胶衬套限制5个方向的自由度,释放一个沿轴向的转动自由度,如图6所示。
实际工况中,汽车运动时稳定杆两端受到一对大小相同,方向相反且垂直于端面的载荷,该载荷的确定与具体的工况有关。根据公司所提供的某车型配置的横向稳定杆,要求在两端施加大小为4 kN,方向相反的力载荷,并基于该载荷作为横向稳定杆的刚度与强度评价标准。在Abaqus中,分别在参考点RP-1、RP-2中设置−4 kN、4 kN载荷,如图7所示。
3.6. 稳定杆强度分析
本文中强度校核是通过有限元分析得到模型的应力结果,观察模型中所有节点的应力值与材料的屈服强度进行比较,若所有节点应力值均小于其材料的屈服强度,则说明该模型符合使用要求,反之则说明不符合产品要求。
通过分析图8中稳定杆的应力云图可以得到:金属稳定杆的最大应力为818.6 Mpa,且应力集中在橡胶衬套支撑位置,故该位置在稳定杆在长期运动过程中容易发生疲劳损坏,然而该金属稳定杆的材料屈服强度为1391 Mpa,因此该金属稳定杆满足强度可靠性要求。复合材料稳定杆的最大应力为174.2 Mpa,最大应力集中在施加载荷的端部位置,该复合材料稳定杆的材料屈服强度为2286 Mpa,有限元分析得到的应力远小于其材料屈服强度,因此该复合材料稳定杆充分满足强度可靠性要求。复合材料稳定杆相较于金属稳定杆,应力明显降低且杆身部分应力都相对均匀分布,并未出现应力集中的部位,强度可靠性更高。
 (a)
(a) (b)
(b)
Figure 8. Stabilizer bar stress cloud diagram. (a) Stress nephogram of metal stabilizer bar; (b) Stress nephogram of composite stabilizer bar
图8. 稳定杆应力云图。(a) 金属稳定杆应力云图;(b) 复合材料稳定杆应力云图
3.7. 稳定杆刚度分析
分析稳定杆的刚度时,忽略稳定杆过度圆角和橡胶衬套弹性变形的影响,主要研究稳定杆在外界载荷的作用下的位移量大小,刚度计算模型如图9所示。稳定杆的刚度计算公式为:
(13)
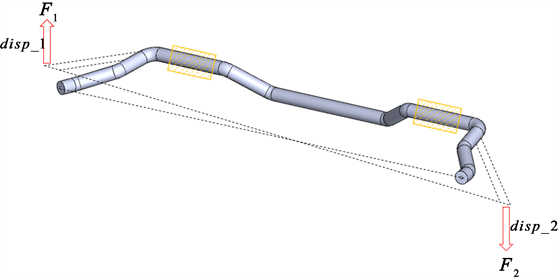
Figure 9. Stabilizer stiffness calculation model
图9. 稳定杆刚度计算模型
通过分析图10中稳定杆的整体位移云图得到:稳定杆在载荷作用下,其最大位移量部位均出现在稳定杆两端,这是由于杆身受到衬套的限制作用,且载荷直接作用在端部位置。通过后处理中输出端部参考点的反作用力RF与位移U,得到力–位移曲线,如图11所示。
 (a)
(a) (b)
(b)
Figure 10. Stabilizer rod displacement cloud diagram. (a) Metal stabilizer bar displacement cloud image; (b) Composite stabilizer rod displacement cloud image
图10. 稳定杆位移云图。(a) 金属稳定杆位移云图;(b) 复合材料稳定杆位移云图
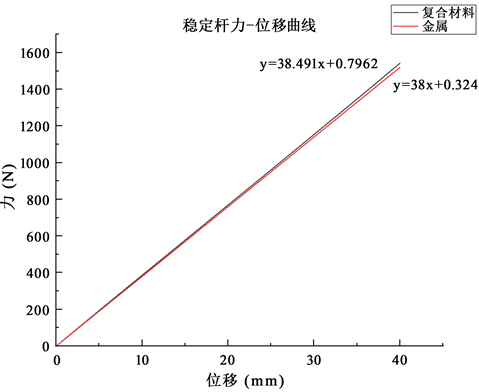
Figure 11. Stabilizer bar force-displacement curve
图11. 稳定杆力–位移曲线
通过分析图11中稳定杆力–位移曲线图可得:复合材料稳定杆刚度为38.49 N/mm,金属稳定杆的刚度为38 N/mm,刚度基本相同。将仿真得到的结果与刚度理论计算结果进行对比如表5所示。

Table 5. Comparison of finite element and theoretical results
表5. 有限元与理论结果对比
3.8. 模态分析
为避免车辆在行驶过程中发生共振现象,影响整车舒适性。分别对金属稳定杆和复合材料稳定杆进行模态分析。同样将模型导入Abaqus中,对稳定杆进行网格划分,赋予材料属性,施加刚度强度分析时的边界条件,对稳定杆的自由度进行限制。由于稳定杆前10阶均为弹性变形,同时前6阶模态接近于0,因此从第7阶模态开始分析。通过后处理得到第7阶至第10阶稳定杆的模态结果如表6所示。

Table 6. Stabilizer rod modal results
表6. 稳定杆模态结果
对比金属稳定杆与复合材料稳定杆固有频率基本一致,因此复合材料稳定杆满足振动要求,不会引发共振。
4. 结论
本文基于能量守恒和层合板理论,得出了±45˚铺层的复合材料稳定杆的刚度解析式。通过有限元模拟比较了金属和复合材料稳定杆的刚度和强度,结果显示在强度满足要求,刚度基本一致情况下,复合材料稳定杆质量降低了52.2%。此外,理论计算结果与有限元分析结果的误差为4.32%,证明了理论的正确性,为复合材料稳定杆的设计提供了有力的参考。
NOTES
*通讯作者。