1. 引言
随着现代化社会科技的快速发展,无线局域网(WLAN, wireless local area network)也即Wi-Fi广泛使用,其通过节点间的通信射频在工业、医疗等无线频段,与其他无线技术相比提供了低成本、高吞吐和便利的无线通信服务。典型的WLAN如图1所示,基本服务集(BSS, basic service set)是WLAN的基本组成部分。每个BSS包含一个专职管理BSS的无线接入点(AP, access point)与多个处于某一特定覆盖区域内的站点(STA, station)。常见的AP有无线路由器、WiFi热点等,手机、笔记本、无线监控、智能汽车等都可以是STA,本文将AP和STA统称为节点,每个节点的发送和接收不能同时发生。各节点共享信道,通过载波侦听多址接入/退避(CSMA/CA, carrier sense multi-access and collision avoidance)的机制避免冲突,称为分布式协调功能(DCF, distributed coordination function)。
对于DCF的性能分析主要有两种研究方法:(1) 建立马尔可夫链模型进行研究,(2) 基于仿真实验方法进行研究。通过阅读相关文献我们可知,一般学者们进行仿真实验大多基于专业的仿真软件,例如NS2、Tiny OS、OPENET等,利用此类软件可以快速精确的设置网络中各个节点参数,例如竞争窗口CW、最大重传次数
,最大退避阶数
等,建立与实际网络相近的网络场景,通过仿真分析系统吞吐S。
然而,马尔可夫链模型能够对影响性能的指标进行理论研究并且能够不断面对新的潜在应用,更加得到了众多学者的青睐。历年来众多的学者对其进行了深入的研究。Bianchi首次利用二维Markov chain对DCF机制所采用的BEB算法进行建模,并得到了系统的饱和吞吐量与冲突概率之间的关系表达式,进而对协议的性能进行分析 [1] 。
Bianchi模型获得了很高的精确度,很多工作在此基础上扩展,Chatzimisios研究了有最大重传次数限制的媒体接入控制(MAC, medium access control)层性能情况 [2] 。Vardakas等人通过控制重传次数和引入退避计时器冻结机制,在饱和状态下进行建模,分析了相关性能指标,得到了更符合协议标准的马尔可夫链模型 [3] ;陈弘原和李衍达在对饱和状态下的Markov系统进行分析时,主要考虑了CW的影响,提出了平均竞争窗口概念 [4] 。Huang和Ivan Marsic介绍了隐藏节点下网络模型和性能分析 [5] 。Chen分析了多速率MAC协议的性能 [6] 。吴峰利用Markov模型分析网络在多速率情况下系统的吞吐量性能 [7] ;杨卫东利用三维马尔可夫链和M/G/1/K队列建立了有限负载下DCF机制的性能模型,分析了终端数量、传输负载、二进制指数回退机制及MAC层有限队列对系统性能的影响,基于该模型,推导了有限负载下最大化吞吐量的最优最小竞争窗口的闭式解 [8] 。Na等人通过对固定竞争窗口协议DCF/CCW的可行性进行分析,针对其DCF机制不能感知信道中处于竞争状态的节点个数问题,提出optimal-DCF/CCW最优化算法,通过估计处于竞争状态的节点个数得到最优竞争窗口与终端数量 [9] ;杨卫东等通过使用队列来表示处于等待发送状态的数据包的数量来模拟网络状态,并借助于Bianchi的二维马尔可夫链模型建立三维Markov模型 [10] ,并且Bae还采用矩阵方法来求解模型处于各个稳定状态的概率,以此来分析网络在非饱和状态下的吞吐量和延时 [11] 。张朝柱等考虑了DCF机制的退避冻结状态及有限的重传次数等问题,提出了一种全新的改进二维Markov链路模型,基于此分析了异构混合业务成分下的DCF机制的性能 [12] 。周礼能将3GPP提出的两种先听后说(LBT)接入机制(即Cat-3和Cat-4)建模为一个二维离散马尔可夫模型,推导出了信号传输失败概率的封闭表达式,并对比分析了捕获效应对两种LBT接入机制的共存系统的性能影响 [13] 。Lin等提出了一种快速自适应碰撞退避(RACB)算法,该算法通过数学模型分析,根据碰撞速率动态调整CW值,得出了RACB使得系统吞吐量在包含任意数量节点的无线环境中接近最大DCF吞吐量 [14] 。随着研究者越来越深入的研究,所建模型已越来越接近现实中的网络。
本文考虑了两个同频AP,在不同的信干比下,两个AP同时回退到0而同时发送数据时,可能会存在同频干扰,导致两个AP的数据传输都失败,基于此,我们将Bianchi模型进行改进,并且引入具有负顾客的双端队列机制,通过刻画状态转移与求解平衡方程得到相关性能指标分析,并通过数值实验和仿真模拟,进一步检验模型的准确性。
2. 方法介绍
2.1. 二进制指数退避算法
为减少节点发生碰撞,节点在DIFS和EIFS之后,采用退避机制,其中二进制退避算法作为IEEE802.11协议的重要组成部分,能有效实现上述目标并提高成功传输数据的概率,进而提高系统的整体性能。
信道空闲时,可能有多个节点准备好了数据,为避免碰撞,节点从
的均匀分布选取一个随机数作为回退数,等待该回退数个时隙长度SlotTime (9 μs)。
(1)
CW的初始值为CWmin,每次数据传输失败后进行重传时,CW翻倍。如果CW达到了CWmax,则保持此值,直到被重置为止。每次数据传输成功时CW重置,开始下一个数据帧的回退。若传输连续失败,重传次数达到r后,数据帧被丢弃,CW重置传输下一个数据帧。可见,重传r次时,无论成功还是失败,CW都会重置。
在数据传输阶段,当回退到0的节点发送一个数据帧,接收节点成功接收到数据之后等待短帧帧间距SIFS (16 μs)后,回复ACK确认帧(32 μs)。如果发送节点收到ACK,则数据发送成功。如果发送数据帧没有被接收节点成功接收,或者ACK发送失败,或者ACK没有被发送节点收到,则数据传输失败,发送节点需要在等待超时后重传数据。等待超时时间ACKTimeout (65 μs)。
在图2中,我们以两个AP,四个STA为例,给出了退避算法过程的示意图。图中CW表示当前阶竞争窗口大小,BO表示随机回退过程时退避计数器从
随机选取的初始值。需要注意的是,图2中的一次传输(Tx, transmission)包含了发送一个数据包和接收一个ACK,一次collision包含了发送一个数据包和等待ACKTimeout时长。帧序列如图3所示,一个数据帧包括PHY头、MAC头和有效载荷payload。
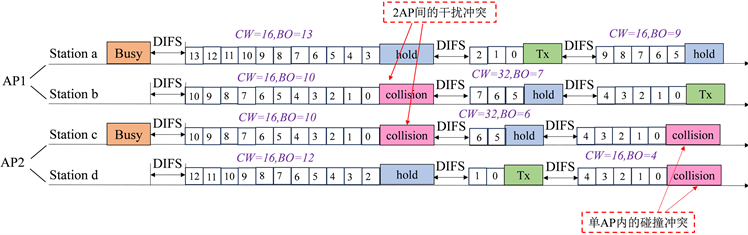
Figure 2. Binary exponential backoff process
图2. 二进制指数退避过程
可以预见的是,在系统负载较小时,通过设定一个较小的CW就能够保证系统的稳定运转;一旦面临大批量信号传输场景,较大的工作负载会直接导致发生碰撞概率的增加,通过设定一个较大的CW,减少了每个节点在其中随机生成相同的退避值的机率,从而降低了发生冲突的概率。此外,规定CW增大至CWmax后保持该值,以及限定了最大重传次数,进一步的确保了网络在大负载下的稳定性。

Figure 3. Frame sequence: (a) Successfully sent; (b) Transfer failed
图3. 帧序列:(a) 成功发送;(b) 传输失败
2.2. 马尔可夫链
Markov过程是作为一类在理性分析和现实应用中都十分有用的随机过程。广泛应用于数学、通信系统以及工程系统等各个领域,并起着十分重要的作用。
定义1:设
是取值在E中的随机过程。如果对于任意的正整数n,
,
及状态
都有
(2)
则称随机过程
为Markov过程。上式为Markov性,也称为无后效性。无后效性是指对于随机过程在
大于
时刻所处状态的概率特性只与
时刻有关,而与之前的状态无关。即
的概率分布只与
的状态有关。
定义2:对于取值于E中的随机序列
,如果对于任意非负整数n及状态
,都有
(3)
则称随机序列
为Markov链,记为
。
3. WLAN网络接入机制建模
对于单BSS,N个STA给AP发送上行数据。Bianchi模型假设理想信道,不会因信道质量差而丢包,所以信道可能处于三种状态:空闲、成功传输、碰撞。本文考虑了2BSS系统,由于可用信道数有限,那么不同的BSS可能会复用同一个信道,而一旦同频AP (使用相同信号道的AP)之间通信区域存在重叠时,会存在相互干扰的情况,于是,在2BSS系统中,信道可能处于四种状态:空闲、成功传输、碰撞、干扰。因此我们基于2BSS系统对Bianchi模型进行了改进。
3.1. 基于负顾客的双端队列机制的Bianchi改进模型
我们令
和
代表t时刻一个节点退避随机过程的退避计数和退避阶数,t是一个离散的虚拟时隙的开始时刻。用i表示一个数据的发送次数,也叫作阶数,r为最大重传次数,m是最大退避阶数,则竞争窗口CW可用下式表示:
(4)
考虑2BSS系统,假设两个BSS系统是完全相同的,我们令
表示AP1中一个数据的发送次数,令
表示AP2中一个数据的发送次数。于是,二维随机过程
可以用二维Markov chain表示,根据r和m的关系,我们分为两种情形,分别如图4和图5所示。
表示二维Markov chain的稳态解。
情形a:当
时,二维Markov chain的状态转移如图4所示,此时,
。
在图4中,
表示碰撞的概率,
表示干扰的概率,那么
则表示一个数据发送成功的概率,不管是碰撞还是干扰,结果都是数据发送失败,所以CW都会重置,于是
就表示数据发送失败的概率。Markov chain的一步状态转移概率为:
(5)
该Markov chain的任意状态之间可达,是不可约的,任意状态到另一状态的步长不存在周期。从任何状态出发,都能到达另一状态,具有常返性。因此该二进制退避过程的非周期不可约,具有稳态解,且所有的稳态概率之和为1。

Figure 4. Markov chain model of DCF (
)
图4. DCF的Markov chain模型(
)
下面,我们利用排队论的知识来求解2BSS系统的稳态概率,因为AP1中的任意状态和AP2中的任意状态互不影响,并且由假设两个BSS系统是完全相同的,所以我们可以求出AP1中的系统稳态概率,再由对称关系,可以得到AP2中的系统稳态概率。
列出系统的平衡方程,如下:
(6)
(7)
(8)
(9)
(10)
(11)
通过迭代和代数运算,能够推出
(12)
根据归一化条件,可以求出此时的
如下:
(13)
其中
(14)
情形b:当
时,二维Markov chain的状态转移如图5所示,此时,
。
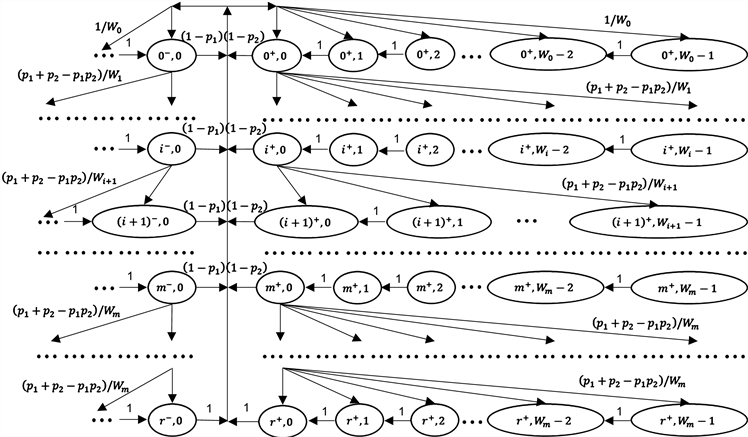
Figure 5. Markov chain model of DCF (
)
图5. DCF的Markov chain模型(
)
同上面的分析,我们首先写出Markov chain的一步状态转移概率为:
(15)
接下来,我们列出系统的平衡方程,如下:
(16)
(17)
(18)
(19)
(20)
(21)
(22)
(23)
(24)
同样通过迭代和代数运算,能够推出
(25)
(26)
再由归一化条件能够得到
(27)
其中
。
节点随机回退到0时发送数据,因此节点在一个时隙发送数据帧的概率为
(28)
其中,当
时,
如(13)所示;当
时,
如(27)所示。
传输数据发生冲突时,至少有另外一个节点也传输数据,共有N个节点,因此条件碰撞概率p可表示为:
(29)
3.2. 双端队列机制下互听2BSS系统吞吐求解
在3.1.节模型的条件下,2BSS系统下的信道将处于空闲和繁忙两种状态,同时在繁忙状态下,该系统或将处于成功和失败,其中失败的原因可能是单AP内的碰撞,也可能是2AP间的同频干扰。本文记空闲状态下的概率为
,繁忙状态下的概率为
,成功的概率为
,失败的概率为
,设2BSS系统下的节点个数为N,当所有节点在一个时隙处在不发送数据帧时,该系统处在空闲状态,因此有:
(30)
故
(31)
当仅有一个节点在发送数据帧时,既不会出现碰撞,也不会出现因2AP同频干扰而导致的失败现象,此时该系统处在成功状态:
(32)
由于系统的稳态的,这代表着各个状态满足归一化条件,从而可以得到
(33)
因此,信道处于三种虚拟时隙的状态概率均可以用
和p表示。
吞吐量(S):数据帧的丢失是不可避免的,但是我们能够降低发生数据帧丢失的概率,通过减少传输过程中信号碰撞和干扰,从而避免浪费大量的信道时间。即信道时间的有效利用程度,可以作为多BSS系统优劣程度的评估标准。在一个信道中,有无数多个工作周期,并且每个周期都是由成功传输前的退避时间和传送数据帧时间所组成。设S表示网络的归一化吞吐量,定义为在一个周期内成功发送有效载荷的信道时间在总的信道时间中所占的比例。
吞吐是单位时间内发送数据有效载荷的比特数,单位bps。吞吐S可以由信道的利用率与物理层速率(单位bps)的乘积表示,
(34)
信道处于三种虚拟时隙的概率可由
和p表示,空闲时隙的长度
是SlotTime。成功传输和碰撞的传输时长分别表示为
和
。
如图3所示,空闲时隙的长度
是Time slot,完成一次成功传输时长
和失败传输时长
分别表示为:
(35)
(36)
其中,
,
。
由式(34)可求得吞吐量S:
(37)
当
时,只有一个节点,不会发生AP内的碰撞,也不会发生2AP间的同频干扰,这种情况下
,因此
。当
时,利用公式(36)和(38),可使得
,令p的初始值为0,不断迭代,使得
接近于
,从而得到p和
的近似解,
假定AP发送包的载荷长度为1500 Bytes,PHY头时长为13.6 μs,MAC头为30 Bytes,MAC头和有效载荷采用物理层速率455.8 Mbps发送,此时
,
,吞吐量S = 30.5。
为进一步研究2BSS系统的性能,当我们固定AP发送包的载荷长度为1500 Bytes时,改变节点N的个数,得到图6所示(8 Mbps = 1 Mb/s),正如预期的那样,理想的情况是不可能发生碰撞,即只有一个传输节点。当节点数量增加时,由于资源争用和CSMA/CA限制,发生碰撞的概率也会增加,整体性能会下降。衰减模式在所有物理层速率情况下都是相似的,即随着节点数的增加,吞吐量会逐渐由最大值下降至稳定。不同的物理层速率下系统的整体性能也不同,当物理层速率越高时,其吞吐量无论是最大值还是之后趋于稳定的值都越大。图7给出了确定节点数为50时,不同物理层速率下有效载荷长度与吞吐量的关系。随着有效载荷长度的增加,系统获得更高的吞吐量直至趋于稳定。因为有效载荷越长,一次能发送的数据就越多,传输等量的数据,需要的传输次数就越少,传输效率提高。当物理层速率增加时,吞吐量最大值也会增加,并且趋于稳定的载荷长度临界值也会增加。
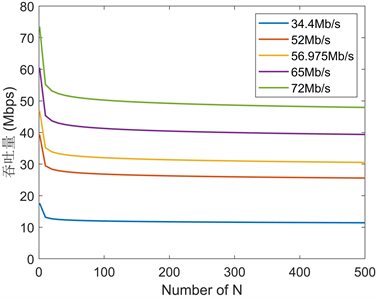
Figure 6. The relationship between the number of nodes and throughput in 2BSS with low SIR
图6. 基于SIR较低的2BSS下节点数与吞吐量的关系
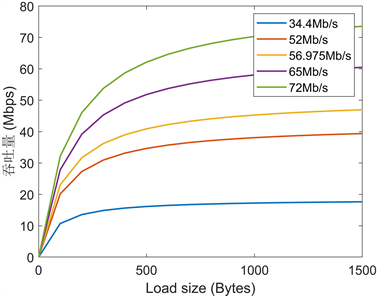
Figure 7. The relationship between payload length and throughput in 2BSS with low SIR
图7. 基于SIR较低的2BSS下有效载荷长度与吞吐量的关系
3.3. 基于SIR较低的互听2BSS系统的仿真
模拟无线局域网络中多个基础服务集之间的竞争和数据传输过程算法步骤,如表1所示。

Table 1. Algorithm steps for multi service set competition and data transmission process
表1. 多服务集竞争和数据传输过程算法步骤
基于上述同等条件下,我们对2BSS系统进行200次的仿真,得到了图8和图9的结果,AP发送包的载荷长度为1500 Bytes,物理层速率为455.8 Mbps,节点N的个数等于500时吞吐量基本处在25至35 Mbps直接,碰撞率在0.3至0.4之间,最终200次仿真得到的吞吐量平均值为31.0281,与前文我们数值实验得到30.5相似;碰撞率平均值为0.351,而前文模型的模拟结果为0.56,模拟得偏大。具体如表2所示。

Figure 8. Simulation of 2BSS throughput based on lower SIR
图8. 基于SIR较低的2BSS吞吐量仿真

Figure 9. Simulation of 2BSS collision rate based on lower SIR
图9. 基于SIR较低的2BSS碰撞率仿真

Table 2. Simulation and results of mutual listening 2BSS system based on double-ended queue mechanism
表2. 基于双端队列机制下互听2BSS系统模拟与仿真结果
3.4. 基于SIR较高的互听2BSS系统建模
当AP发送包的载荷长度为1500 Bytes,PHY头时长为13.6 μs,MAC头为30 Bytes,MAC头和有效载荷采用物理层速率275.3 Mbps发送,吞吐量S = 16.1。当物理层速率保持前文的455.8 Mbps时,吞吐量为43.2,比SIR较低时的系统吞吐量大,即在同频干扰也能传输成功时,系统的吞吐量会变大。
同样我们对在SIR较高的2BSS系统里,不同物理层速率下节点数与吞吐量的关系,如图10所示,为了便于比较,我们取了与上文相同的5个物理层变量:34.4 Mb/s、52 Mb/s、56.975 Mb/s、65 Mb/s和72 Mb/s,
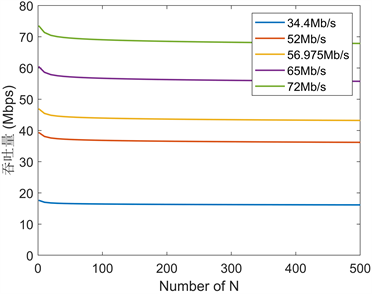
Figure 10. The relationship between the number of nodes and throughput in 2BSS with high SIR
图10. 基于SIR较高的2BSS下节点数与吞吐量的关系
系统的吞吐量在不同的节点数下的趋势与SIR较低情形是一致的,不同点在于由吞吐量最大值逐渐下降达到稳定时的值比上文的结果大,这可能是由于SIR较低的同频干扰会导致传输失败,而SIR较高的系统下,同频干扰时不会失败,系统的传输成功率因此提高,进而吞吐量的稳定值也会提高。图11是基于SIR较高的2BSS下有效载荷长度与吞吐量的关系,与SIR较低情形的结果一致,同时也发现有效载荷长度与吞吐量的关系基本不会受SIR变高的影响。

Figure 11. The relationship between payload length and throughput in 2BSS with low SIR
图11. 基于SIR较低的2BSS下有效载荷长度与吞吐量的关系
4. 总结与展望
在2BSS场景下建模时,基于Bianchi模型,我们创新性地引入具有负顾客的双端队列机制,将两个AP的情况用两个独立的Bianchi模型建立,并在考虑同频干扰时,形象地刻画成湮灭现象。模型求解时通过刻画状态转移与迭代法求解平衡方程,进而得到相关性能指标。对于SIR较低的2BSS系统,随着节点数N的增加,吞吐量会逐渐由最大值下降至稳定,同时当节点数固定时,随着有效载荷长度的增加,系统将获得更高的吞吐量直至趋于稳定。对于SIR较高的2BSS系统,不管是节点数还是有效载荷长度,其对吞吐量的影响趋势是一致的,不同的是此时稳定后的吞吐量要比前一种情形大,原因就是SIR较高时同频干扰不会导致数据传输失败。但是改进的Bianchi模型,其适用场景相对局限,仅仅只能考虑两个AP相互干扰的情况,在面对更多的BSS场景下,模型的推广难度较大。
本文研究工作主要由Bianchi模型及排队论与平衡方程迭代求解为基础作为展开,可以预见的是,在人工智能技术飞速发展的当下,未来在多BSS场景下WLAN网络信道接入机制的建模方面,将会结合先进的技术,如人工智能、深度学习、频谱感知等,以实现更智能、高效和安全的信道接入机制,从而提升WLAN网络的整体性能和用户体验。