1. 引言
根据《普通高中数学课程标准(2017年版2022年修订)》(以下简称新课标)指出:“数学核心素养是数学课程目标的集中体现,是具有数学基本特征的思维品质、关键能力的集中体现,是在数学学习和应用中逐步发展的” [1] 。新课标的出台使先前以知识的了解、理解与记忆为目标的教学转变为着重培养学生的学科核心素养。数学教学要以核心素养为出发点和落脚点,密切围绕核心素养开展,使课堂教学从以知识教学为本转向以培养学生核心素养为本。
传统的课堂教学模式存在以活动为导向的教学和灌输式教学两大误区,学生知识的输出往往是通过回忆、再现以及模仿的方式。在这种模式下,课堂教学缺乏大概念的引导,学生不能将所学知识迁移到现实情境中,缺乏智力的提升。学生的理解能力是学生能否对知识进行迁移的重要指标,是评估数学核心素养的表现之一,为贯彻落实核心素养,传统的基于“是什么”和“为什么”的教学已经无法满足学生智力增长的要求。因此在理解的基础上进行教学设计,从教学目的出发、关注教学评价设计教学更能够满足培养核心素养的要求。
单元的大概念和基本问题是什么?学生在学习时的学习目标和预期结果是什么?有哪些明确的证据可以证明学生“理解”了知识,达到了学习目标、预期结果?这些证据能否对教师的教学做出有效反馈?需要准备哪些材料来设计教学?我们必须以始为终,关注教学目标和教学评价,使教师教学和学生学习按照一个正确的方向前进。
基于以上问题的分析,笔者将以美国课程与教学领域的专家Great Wiggns和Jay McTighe提出的UbD理论为依据,探索提升核心素养的逆向教学设计。
2. UbD理论概述
UbD理论(Understanding by Design)是由美国格兰特·威金斯和杰伊麦格泰提出针对传统教学的弊端提出的一种教学设计理论,译为“基于理解的设计”。理论主要包括三个方面:构建理解的框架、“逆向”教学设计、将理论融入教学实践。
2.1. “理解”和“逆向”的思想
“理解”不同于“知道”,它是对知识的深度学习,是智力的建构,理解意味着行动,它是一系列关键能力的综合。布鲁姆曾指出理解的核心是表现力,这种表现力即知识的迁移能力。理解的目的就是用已获得的知识去揭示事实背后所隐藏的方法和含义并加以应用 [2] 。“逆向”即从教学目标和预期学习结果出发设计教学。崔允漷教授也指出从期望学生“学会什么”出发,逆向设计“学生何以学会”的过程,为学科核心素养的落地指明了清晰的路径 [3] 。
2.2. 理解六侧面
UbD理论将“理解”分为六侧面,如表1所示 [4] ,通过六侧面学生达到了六侧面就说明学生达到了对知识的“理解”。

Table 1. Understand the meaning of the six sides
表1. 理解六侧面的含义
2.3. 大概念和基本问题
“理解”强调大概念,大概念是理解的核心,是迁移的基础。大概念作为上位概念,能够帮助学生零碎的知识整合起来,构建起一个知识体系。它不仅打通学科内和学科间的学习,还打通学校教育与现实世界的路径 [5] 。基本问题能够有效激发学生思考和主动探究,帮助学生理解,促进知识迁移,将之前所学知识调动起来用于解决新问题,这在一定程度上还能够帮助学生架构起有逻辑的知识体系。最优秀的单元设计为学生提供了许多机会使学生以自己的方式探讨问题和观点 [6] 。
2.4. 评估与反馈
教师要像“评估员”一样思考,思考有哪些证据证明了学生“理解”,即确定合适的评估方式证明学生达到了预期学习结果。UbD理论强调评估设计要建立在教学活动之前,主张在传统的评估方式的基础上设计多样化的评估方式,如:表现性任务、学生互评和自评等。评估不仅要求多样化的形式,还要根据不同性质的知识内容设计不同层次的评价方式,从而反映学生对知识“理解”的深度和广度。
2.5. UbD理论教学设计框架
UbD理论指导下的教学设计分为三个阶段,设计框架如图1所示。明确目标、理解六侧面以及基本问题作为制定第1阶段教学设计的重要支撑,以帮助学生和教师明确学习和教学目标。而理解六侧面不仅涉及阶段1,在阶段2中也是不可或缺的内容。阶段2需要确定合适的评估标准,从而让教学结果得到适时的检验与反馈。在确定好学习目标和评估标准后,需要开始规划具体的教学过程,即阶段3的设计,也是是逆向教学设计中的核心环节。阶段3根据WHERETO的元素对应三角函数的具体内容,分层设计教学。
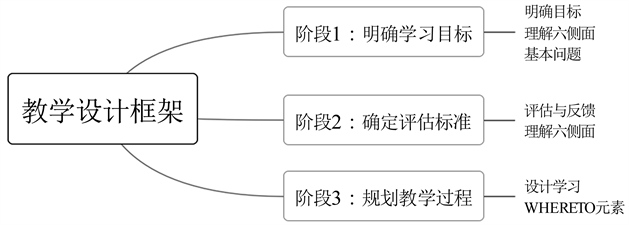
Figure 1. UbD theoretical instructional design framework
图1. UbD理论教学设计框架
3. 阶段1的教学设计

Table 2. Phase 1 design of “Trigonometric function” reverse unit design
表2. “三角函数”逆向单元设计的阶段1
笔者根据UbD理论,以三角函数这一单元为例设计教学。三角函数在数学领域有着独特的作用,特别是在微积分出现以后,三角函数是多个领域中最常使用的描述曲线运动的数学理论 [7] 。三角函数是在学习了指数函数和对数函数后所开设的单元,此时学生已经掌握了学习函数的一般过程和思维方式,能够较好地运用数形结合思想并能够将函数知识与生活实际相联系。该教学设计采用单元教学,以期规避单课教学使得数学概念孤立分散、轻重不分、认识肤浅等问题 [8] 。
根据三角函数的知识结构、逆向教学设计的要求以及课程标准,从教学目标、基本问题以及预期的理解等方面设计第1阶段的教学,具体的设计见表2。
4. 阶段2的教学设计
学生对知识的理解状况需要确定合适的证据来证明,也就是建立教学评价。根据逆向教学设计的要求教师要教学评价要在教学实施之前进行设立。合适的证据从表现性任务和其他任务两方面制定,学生在完成任务的过程中,知识的理解和掌握程度得到检验,具体的任务设置如表3所示:

Table 3. Phase 2 design of “Trigonometric Function” reverse unit design
表3. “三角函数”逆向单元设计的阶段2设计
制订表现性任务时以六侧面为依据,任务2中没有新同学时可以改为同桌互相交流自己所建构知识的过程,教学设计要依据具体的课堂情况做出灵活调整。
5. 阶段3的设计
阶段3是在经历预期结果和合适证据的确定后,为了达到预期的教学效果而设计的教学活动,该部分以Great Wiggns和Jay McTighe 提出的“WHERETO”为依据,对每个元素进行解释说明(如表4 [9] 所示),以元素为基础对应设计教学过程。因此阶段3的设计有助于帮助设计者构建和检测学习计划,使得预期的目标、评估方法以及证据在整个单元教学中实现贯彻融合 [10] 。

Table 4. “WHERETO” elements and their interpretation
表4. “WHERETO”元素及其解释
在设计第3阶段教学时,根据WHERETO中各元素的要求,将所要掌握的三角函数的知识设计成任务和一系列问题串,并联系三角函数发展史和生活中的实际问题,贯彻数形结合思想,从而让学生深刻掌握知识,达到知识迁移和灵活运用的水平。如表5所示,教师要注意将教、学以及评价三个方面相互融合,培养学生自主学习和探究的能力,并能够对知识的进行迁移及运用。此阶段让学生的思考探究、反馈评价贯穿整个教学过程,从而形成一个以学生为主体的教学计划,充分调动学生的主动性。根据WHERETO设计教学,能够有效帮助教师设计适合新课标以及核心素养要求的课堂。

Table 5. Stage 3 design of inverse unit design of “Trigonometric Function”
表5. “三角函数”逆向单元设计的阶段3设计
6. 反思与启示
6.1. 教学设计从经验型转向实证型
逆向设计以结果为导向,通过优先对教学评价的思考让教师对知识的理解更加深刻,通过问题架构教学目标。逆向设计引起的教学结构的变化使教材真正成为一种“材料”,让教师从“教教材”走向“用教材” [11] 。学生在这种教学模式下,不仅能够获得知识,还能亲身参与到知识的探究和构建,提高自身的学习能力和核心素养。
6.2. 强调知识的理解和迁移
理解知识是能够灵活运用知识的前提,是迁移的基础。布鲁纳指出,理解是超越信息本身的,当能够真正理解知识,就能够将知识迁移到实际的情境或者其他学科中,充分发挥知识的价值。教师的教学要聚焦学生对知识的理解和迁移能力的培养,学以致用,充分发挥知识的现实价值。
6.3. 完善教师队伍
UbD理论为教师的教学设计提供了模板,但具体的、要落实到课堂中的教学设计需要教师根据不同的单元、学生的不同情况进行设计与完善,需要教师对理论做到充分地理解并将其内化。此外一个完善的教学设计需要教师群体的通力合作和精心设计,全面提高教学的质量和效率。
基金项目
黄冈师范学院2023年校级教学研究项目立项课题“深度学习视域下中学数学课堂提问的有效性研究”(项目编号:2023CE22)。