1. 引言
近几年新能源的发展进入高峰期,氢能作为一种重要的清洁能源,其相关产业迎来了新的发展机遇。氢燃料电池的零排放、效率高、功率密度大、燃料加注方便等特点使得其成为新能源汽车行业关注的焦点,但是氢燃料电池动态响应慢,而且在大功率状态下电压会降低,无法直接向负载供电 [1] [2] 。因此,针对于氢燃料电池的DC/DC大功率变换器也应运而生,与光伏发电等行业的应用不同的是氢燃料电池所用的DC/DC变换器需要保证纹波电流要足够小,因为纹波电流过大会对氢燃料电池产生的严重的寿命影响 [3] 。由于DC/DC流过的直流电流较大,其电感磁芯中存在较大的直流磁通分量,加上对纹波要求较高,这导致电感体积过大 [4] ,为解决这个问题,反向耦合电感的Boost电路被提出,因为电感的反向耦合,其磁通纹波分量相互增强,可以降低纹波,减小电感体积 [5] 。而在DC/DC变换器设计中,最重要的就是电感参数的计算,现阶段常见的方式为通过既定参数计算耦合电感参数,对于电感参数变化对系统产生的影响并没有分析 [6] ,而且针对于电感参数的确定,大多数研究方式为通过仿真软件修改参数,观测系统结果的变化,难以寻找到最优解。
本文针对于氢燃料电池用DC/DC变换器,通过系统化建模的方式分析了耦合电感的参数对于DC/DC变换器的纹波的影响,进而选取最优的耦合电感设计参数。同时所建立的模型可以用于研究其他参数对于整个系统性能的影响,为系统设计提供指导意义。
2. DC/DC工作原理分析
本文以升压DC/DC变换器为例,其拓扑结构如图1所示。
为增大通过电流,采用多路并联的方式,每一路包含两相,每一相中的拓扑和硬件结构完全相同,且两相输入滤波电感反向耦合。以四相交错并联为例,每一路中的两相驱动信号相差180˚,两路的驱动信号相差90˚,其拓扑结构如图2所示。
其中,输入电源为Vin,总输入电流为Iin。第一相至第四相的电感分别为L1、L2、L3、L4,电感值都相同,等于Lp。L1和L2之间、L3和L4之间的耦合系数为kp,互感为Mp。通过四相的电流分别为I1、I2、I3、I4。
互感系数和互感的关系为:
(1)
Boost电路工作时,定义驱动信号为G1、G2、G3、G4,四路驱动信号之间相位相差90˚。以G1为参考,G2、G3、G4的相位分别为180˚、90˚、270˚,驱动信号示意图如图3所示。
3. 电感参数设计
3.1. 电路模型分析
通过建立电路的电流电压关系,以获取电感设计相关参数在电路中的作用。
由图2可以得出电流之间的关系,如式(2)所示。
(2)
电流的导数如式(3)所示。
(3)
令
(
),
为电流
的电流变化率。则可将式(3)写作式(4)。
(4)
假设每一路Boost电路工作在电流连续模式,根据KVL定律,列写每一相的环路电压方程,如式(5)所示。
(5)
其中
为开关函数,见式(6)。
(6)
在不同的开关状态下,确定
的值,然后带入到式(5)中,解方程组即可以得到不同状态下电流的变化率。
3.2. 开关模态分析
通过对系统开关模态的分析,计算出每一相的电流变化率,进而计算纹波电流与各参数的关系,最终确定电流峰峰值与电感相关参数的关系。
3.2.1. 电流变化率计算
列出每个状态下四相的KVL方程进行求解。
计算得出的相电流电流变化率见式(7)~(10)。
(7)
(8)
(9)
(10)
计算得出的路电流电流变化率见式(11)~(12)。
(11)
(12)
3.2.2. 不同开关模态的持续时间
在3.2.1节中对不同开关模态下的各相电流的变化率进行了分析和计算。如果再计算出不同模态的持续时间,就可以计算电流变化率在时间上的积分,得到各个电流的纹波电流波形,并计算出电流纹波的峰峰值。经过分析计算,得出了开关模态的持续时间如表1所示。

Table 1. Duration of different switching modes
表1. 不同开关模态的持续时间
3.3. 纹波电流计算
在3.2节中对不同模态,不同占空比下各相电流斜率和开关模态的持续时间进行了计算,然后可以通过式(13)来计算各相电流在不同占空比下的纹波电流波形。
(13)
计算出纹波电流的波形后,可以根据纹波电流波形计算出纹波电流的峰峰值。因为四相电流波形相同,只是相位相差固定角度。因此本文以第一相电流
来计算相电流的峰峰值。通过对各相电流在各个模态下的变化率和持续时间的计算分析,以及电流变化阶段的分析计算,可以计算出各相电流的峰峰值。以电流上升阶段或下降阶段来计算电流的峰峰值,相电流峰峰值
和路电流峰峰值
计算结果分别见式(14)和(15)。
(14)
(15)
3.4. 电流峰峰值与电感参数的关系
通过以上章节对电路模态、电流变化率以及电流峰峰值与各参数之间关系的分析,可以利用工程计算软件根据上面介绍的方法计算出相电流峰峰值
、路电流峰峰值
与占空比d、输出电压
、相电感
、相电感耦合系数
之间的数量关系。根据设计需求,依据电流峰峰值与电感参数的关系,选择合适的相电感大小和耦合系数。
4. 试验验证
根据计算,选择电感为300 uH,耦合系数为0.6,结构设计采用“EIE”结构,磁芯材料为铁硅铝磁粉,气隙结构为分布式,测试平台为大功率DC/DC变换器,设计纹波电流 ≤ 1%。
DC/DC变换器输入电压为300 V,输出电压为600 V,输入电流为200 A。测试结果如图4所示。其中CH1-2为1、2相MOS管的Vgs电压,CH3-6为1、2、3、4相MOS管的Vds电压,CH7、CH8为第1、2相电感电流,由测试结果可知,实测波形与计算分析一致。
纹波测试如图5所示,其中CH1-4为1、2、3、4相MOS管的Vds电压,CH5、CH6为3、4相耦合电感电流,CH7为总输出电流,CH8为总输入电流。通过示波器可以读出所测总输入电流峰峰值为6 A,平均值为405.4 A,由此计算得到输入电流纹波为0.74%。
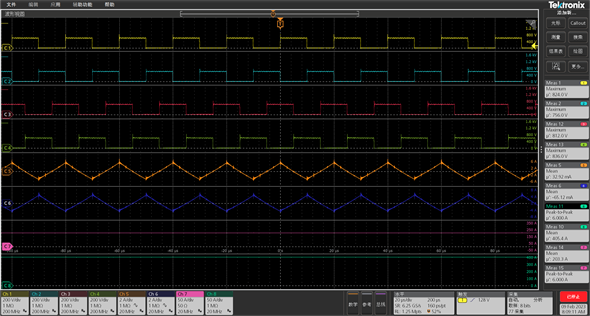
Figure 5. Peak to peak test result graph
图5. 峰峰值测试结果图
5. 总结
本文介绍了一种应用于交错并联电路的反向耦合电感的设计方法,通过分析开关模态、分析电流变化率、计算电流纹波,从而获取电流纹波与耦合电感参数的关系表达式,从而选择合适的耦合电感参数。即通过系统化建模的方式,可以准确地根据项目指标选择耦合电感参数最优解,本文介绍的耦合电感参数设计方法是电感设计的基础,具有重要参考价值。
参考文献