基于SSA-GRU深度学习优化模型的短时公交客流预测

Short-Term Bus Passenger Flow Forecasting Based on SSA-GRU Deep Learning

摘要: 短时公交客流预测是实时动态调整公交发车频率，实现公交精准动态调度的重要决策基础之一。为挖掘公交客流的时序特征，提升短时公交客流预测精度，建立了一种基于麻雀搜索算法(Sparrow Search Algorithm, SSA)优化门控循环单元(Gated Recurrent Unit, GRU)的短时公交客流预测模型。该模型基于历史客流数据的时序分布特征，利用SSA寻优算法对GRU中的隐含层节点个数、学习率和训练次数进行寻优，然后依据参数寻优结果重构模型超参数，利用门控循环神经网络基进行短时客流预测。为验证优化模型的预测性能，选取某城市1号线站点客流数据进行实验；结果表明，相比于GRU门控循环神经网络，SSA-GRU模型的平均相对百分误差(MAPE)降低了37.9%、平均绝对误差(MAE)降低了42.1%，均方根误差(RMSE)降低了40.7%，组合模型的预测精度高于GRU模型且能够有效进行短时公交客流预测。

Abstract: Short-term bus passenger flow prediction is one of the important decision bases for real-time dy-namic bus frequency adjustment and accurate dynamic bus scheduling. In order to mine the time series characteristics of bus passenger flow and improve the prediction accuracy of short-term bus passenger flow, a short-term bus passenger flow prediction model based on Gated Recurrent Unit (GRU) optimized by Sparrow Search Algorithm (SSA) was established. This model was based on the historical passenger flow data of time series distribution. Firstly, SSA optimization algorithm was used to optimize the hyper parameters of GRU, such as hidden layer nodes, learning rate and train-ing times. Then, based on the parameter optimization results, short-term passenger flow prediction was carried out by using gated recurrent neural network. To verify the predictive performance of the optimized model, the passenger flow data of Line 1 station in a city were selected for experi-ment. The results show that compared with the GRU gated recurrent neural network model, the Mean Absolute Error (MAE) of the SSA-GRU model is reduced by 42.1%, the Root Mean Square Error (RMSE) is reduced by 40.7%, and the Mean Relative Percentage Error (MAPE) is reduced by 37.9%. The combined model can effectively predict short-term bus passenger flow. The results show that compared with the GRU gated recurrent neural network model, the Mean Absolute Error (MAE) of the SSA-GRU model is reduced by 42.1%, the Root Mean Square Error (RMSE) is reduced by 40.7%, and the Mean Relative Percentage Error (MAPE) is reduced by 37.9%. The combined model can ef-fectively predict short-term bus ridership, and the prediction accuracy is higher than that of the GRU model.

1. 引言

发展公共交通是缓解城市交通拥堵的重要途径之一，公交出行在公共交通系统中发挥主导作用，站点与线路设计规划不完善，公交车辆超载与空车现象频发，降低了城市公交的运营服务水平。精确、实时的短时客流预测是优化公交调度和制定合理排班方案的前提与基础，为市民提供高效公交出行服务，优化公交资源的动态配置。

近年来，基于深度学习网络的短时客流预测方法被提出和实践，相较于传统预测方法，深度神经网络可以挖掘数据中复杂的非线性关系，对数据的分布式特征进行提取。循环神经网络(Recurrent Neural Network, RNN)将神经元前一刻的输出再次转化为输入信息，通过共享其网络结构中的参数，提升了训练性能，使模型可以提取不同长度数据的分布特征；如Ran X等 [1] 将卷积神经网络(CNN)中的池化层铺与全连接层相连，提取数据特征，预测效果得到提升。由于RNN存在周围的客流进行预测，并改进激活函数来提高预测精度；李高盛 [2] 等基于LSTM网络对时段内各公交站点展开客流预测；龚兰兰等 [3] 提出通过建立多公交站点的客流时空矩阵来分析公交客流时空分布上的变化；Hao等 [4] 发现神经网络模型在处理大量数据时，存在训练时间长等缺陷，改进后的LSTM网络提高了短时客流预测效果；Liu等 [5] 利用深度长短时记忆神经网络(DLSTM)开展客流量预测，伴随DLSTM模型深度的增加，预测性能进一步得到提升。Wan Huaiyu等 [6] 在LSTM网络框架的基础上，创建了一种新的存储单元，提出了CTS-LSTM模型(Correlated Time Series oriented LSTM, CTS-LSTM)。Ouyang Qi等 [7] 结合实时信息，基于北京市公交站点客流历史实时数据利用LSTM进行实时预测。温惠英等 [8] 基于双向长短时记忆网络(Bi-LSTM)对广州地铁某站进站客流进行预测，由于LSTM网络由三个门结构组成，训练难度较高，而门控循环单元网络GRU的结构更为简单，模型参数较少、训练时速度更快；如侯晓云等 [9] 分别使用LSTM模型和GRU模型对客流OD进行预测，结果表明在预测精度大致相同的情况下GRU模型的收敛速度更快。；李梅 [10] 研究短时公交客流预测的过程中，对比分析了LSTM网络、GRU门控单元与DBN网络三种模型，采取不同的时间粒度进行预测，结果表明，GRU的预测精度优于DBN和LSTM；梁强升等 [11] 建立了GCGRU预测模型，该模型将GRU模型与CNN网络组合，提高了模型的预测性能。由于短时客流数据变化特征的非线性不确定性，单一预测方法的都存在一定的限制，因此诸多学者使用不同模型弥补缺陷，提高预测精度和性能；蔡昌俊 [12] 采用小波变换与Adam算法优化LSTM网络，建立了WT-LSTM模型，提高了模型预测精度；李聪聪 [13] 利用POI数据对站点用地性质进行了分类，通过CEEMDAN-PSO-BiLSTM模型对站点短时客流进行了预测；罗嘉诚 [14] 建立了CNN-GRU组合模型，经验证模型能有效的提取客流数据的时空分布特征。石敏莲等 [15] 使用主成分分析法提取客流特征，构建了PCA-LSTM组合模型，提高了预测精度。赵阳阳等 [16] 把经验模态分解法与LSTM模型相结合，对上海地铁进站客流进行了分析预测，验证模型预测效果。Ma Xiaolei等 [17] 把CNN网络与Bi-LSTM进行组合，分别提取客流数据的空间和时间特征，对北京地铁各站点开展了短时客流预测。

综上，在短时客流预测领域各深度学习模型得到了广泛应用，并取得了良好的成效。然而，深度神经网络模型的超参数选择多采用人工调优方式，具有一定的主观性，影响模型的预测性能。基于上述问题，本文提出SSA-GRU组合预测模型，通过SSA优化算法对GRU模型的超参数(隐含层节点、学习率和训练次数)进行寻优并开展短时客流预测，构建了基于深度学习超参数优化的短时公交客流预测模型，以期提高短时客流预测精度。最后通过比较不同模型的预测性能，验证组合模型的有效性，为调整公交发车频率、优化公交调度等提供依据。

2. 问题描述

公交短时客流具有较强的时间相关性，随着短时客流数据的非线性与不稳定性增强，传统线性模型难以有效提取数据中的时序特征，致使预测精度较低；门控神经网络(GRU)能够有效挖掘客流数据的非线性特征，处理复杂的时间序列数据，结构简单、训练速度块，能够有效提升公交客流的预测效率及精度。但GRU神经网络中超参数的设定多采用人工经验调参，存在一定的主观性，影响模型的预测性能；麻雀搜索算法(SSA)的收敛速度快、寻优能力强，因此引入SSA优化算法对GRU神经网络中的超参数进行寻优，以最优超参数构建门控神经网络进行短时客流预测。假设数据时间窗步长为n，利用历史客流数据 $X=\left(x_{t-1},x_{t-2},\cdots ,x_{t-n}\right)$ 对下一间隔的客流 $x_t$ 进行多步预测，即：

$x_t=P\left(x_{t-1},x_{t-2},\cdots ,x_{t-n}\right)$ (1)

式中， $P(\cdot )$ 表示建立的预测模型；n = m，m为可设置的时间步长。

3. 模型构建

门控神经网络(GRU)可以有效挖掘数据的时序特征，被广泛运用在时间序列预测中，但其网络中超参数的设定存在主观性，本文通过SSA优化算法对GRU模型的隐含层节点个数、学习率和迭代次数等超参数进行寻优，构建SSA-GRU组合预测模型，开展短时公交客流预测。

3.1. 门控循环单元神经网络

门控循环单元神经网络(Gated Recurrent Unit, GRU)由Chung等在2014年提出 [18] ，可以避免长序列数据在训练过程中发生梯度消失和梯度爆炸。GRU神经网络通过“门控”结构可以选择性保留或遗忘历史信息，适用于在时间序列预测中挖掘数据特征。

GRU通过更新门(update gate)和重置门(reset gate)两个门控循环结构记忆输入信息的特征，控制门控循环单元的输出。由于GRU只有2个控制门，在训练中可以降低运算的复杂度，提升训练效率。整体框架如图1所示：

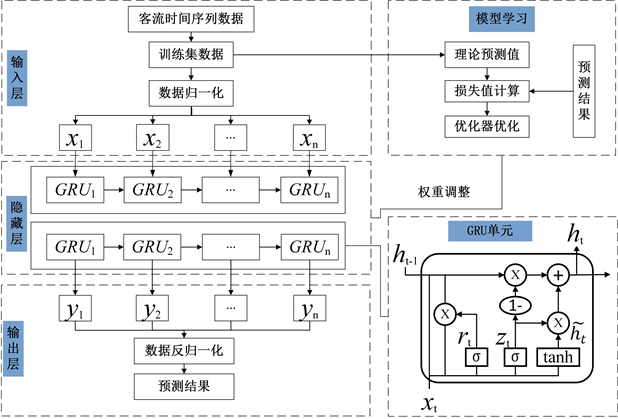
Figure 1. Structure of the GRU prediction model

图1. GRU预测模型的结构

GRU的工作原理及计算公式如下：

(1) 更新门

更新门 $z_t$ 决定所保留前一个时刻信息特征的大小，如式(2)所示：

$z_t=\sigma \left(W_Z\cdot \left|h_{t-1},x_t\right|+b_z\right)$ (2)

式中： $z_t$ 为更新门信息； $\sigma$ 为sigmoid激活函数，将更新门和重置门数据信息转化为[0,1]范围的数值； $x_t$ 表示t时刻的输入信息； $h_{t-1}$ 为 $t-1$ 时刻的隐藏层状态(隐藏状态充当了神经网络记忆，包含之前节点所保留的数据信息)； $W_z$ 为更新门中的权重矩阵， $b_z$ 代表更新门的偏置项。

(2) 重置门

重置门 $r_t$ 决定前一时刻的信息特征需要被遗忘的程度，计算公式如下：

$r_t=\sigma \left(W_r\cdot \left|h_{t-1},x_t\right|+b_r\right)$ (3)

式中： $r_t$ 代表重置门信息； $W_r$ 表示重置门里的权重矩阵； $b_r$ 代表重置门中的偏置项；其它符号同式(2)。

(3) 计算候选隐藏状态

重置门 $r_t$ 决定所需传递的记忆信息的数量大小，并继续向前传递新的记忆信息，计算公式如下：

${\bar{h}}_t=\tanh \left(W_{hr}\cdot \left|r{\otimes }_t{h}_{t-1},x_t\right|+b_n\right)$ (4)

式中： ${\bar{h}}_t$ 为当前时刻的候选隐藏状态；tanh为双曲正切激活函数，通过这个函数可以将数据转换为[−1,1]范围的数值； $\otimes$ 表示Hadamard乘积； $W_{hr}$ 与 $b_n$ 分别为权重矩阵和偏置值。

(4) 确定当前隐藏层保留的信息

利用更新门保留当前单元的隐藏层状态信息并传递到下一个单元，如式(5)所示：

$h_t=z_t\otimes {\bar{h}}_t+\left(1-z_t\right)\otimes h_{t-1}$ (5)

式中： $h_t$ 为当前时刻的隐藏状态。

最后，输出GRU当前时刻的公交客流预测值：

$y_t=\sigma \left(W_y{h}_t+c\right)$ (6)

式中： $y_t$ 为t时刻短时公交客流预测值； $W_y$ 为隐含层状态与 $h_t$ 网络输出 $y_t$ 间连接权值；c为偏置值。

3.2. 麻雀搜索优化算法

麻雀搜索算法(Sparrow Search Algorithm, SSA)为新型群智能仿生优化算法，其模拟了麻雀种群在觅食途中不同个体间的分工和社会互动，通过局部或全局搜索最优值，收敛速度快、寻优能力强 [19] 。算法步骤如下：

Step1：初始化麻雀种群，设置算法迭代次数、发现者与加入者比例、种群规模等。

Step2：计算种群适应度 $F_s$ ，如式(7)所示。

$F_s=\left[\begin{array}{cccc}f(s_{1,1}& s_{1,2}& \cdots & s_{1,d})\\ f(s_{2,1}& s_{2,2}& \cdots & s_{2,d})\\ & ⋮& & \\ f(s_{n,1}& s_{n,2}& \cdots & s_{n,d})\end{array}\right]$ (7)

式中：n为麻雀数量；d为待优化问题变量的维数，即待优化超参数的个数； $s_{n,d}$ 表示第n个麻雀在第d维的位置，即待优化超参数(隐含层节点、训练次数与学习率)的取值；模型中，每一只麻雀的位置代表一个解，该位置食物浓度的高低即适应度值的大小，代表解的优劣。

将适应度函数定义为短时客流预测值和实际值的均方误差，如式(8)所示：

$E\left(f\right)=\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{\left(x_i-y_i\right)}^2}$ (8)

式中：n为训练样本数； $x_i$ 表示客流的实际值； $y_i$ 表示客流的预测值。

Step3：更新发现者位置。

$S_{i,j}^{t+1}=\{\begin{array}{ll}{S}_{i,j}^t\cdot \exp \left(-\frac{i}{\alpha \times ite{r}_{\max }}\right),\hfill & \text{if}{R}_2<ST\hfill \\ S_{i,j}^t+Q\cdot L,\hfill & \text{if}{R}_2\ge ST\hfill \end{array}$ (9)

式中：t表示当前时刻的迭代次数； $i=1,2,\cdots ,n$ ； $j=1,2,\cdots ,d$ ； $S_{i,j}^{t+1}$ 表示在t + 1次迭代时第i只麻雀j维空间里的位置；R₂代表预警阈值；ST代表安全阈值； $ite{r}_{\max }$ 为最大迭代次数；Q是正态分布的一个随机数，L表示全一矩阵， $\alpha$ 是(0,1]中的随机数。

Step4：更新加入者位置。

$S_{i,j}^{t+1}=\{\begin{array}{ll}Q\cdot \exp \left(\frac{X_{worst}^t-X_{i,j}^t}{i^2}\right),\hfill & \text{if}i>\frac{n}{2}\hfill \\ S_p^{t+1}+\left|S_{i,j}^t-S_p^{t+1}\right|\cdot A^{+}\cdot L,\hfill & \text{otherwise}\hfill \end{array}$ (10)

式中： $S_p$ 表示发现者所在的最优位置； $X_{worst}^t$ 代表全局搜索过程中出现的最差位置；A代表元素为1或−1的1 × d矩阵； $A^{+}=A^{\text{T}}{\left(A{A}^{\text{T}}\right)}^{-1}$ 。

Step5：更新警戒者位置。

$S_{i,j}^{t+1}=\{\begin{array}{ll}{S}_{best}^t+\beta \cdot \left|S_{i,j}^t-S_{best}^t\right|,\hfill & f_i>f_g\hfill \\ S_{i,j}^t+K\cdot \left(\frac{\left|S_{i,j}^t-S_{worst}^t\right|}{(f_i-f_w+\epsilon )}\right),\hfill & f_i=f_g\hfill \end{array}$ (11)

式中： $S_{best}^t$ 表示全局搜索中的最优位置； $f_i$ 代表当前的适应度值； $\beta$ 是步长控制参数； $\epsilon$ 代表不为0的常数；K是[−1,1]中的随机数； $f_w$ 和 $f_g$ 分别为全局搜索中的最差和最佳适应度值。

Step6：更新全局搜索过程中的最优适应度值。

Step7：执行步骤2-6，直到满足最大迭代次数，输出全局搜索过程中发现的最优个体位置与适应度值，完成优化。

具体流程如图2所示：

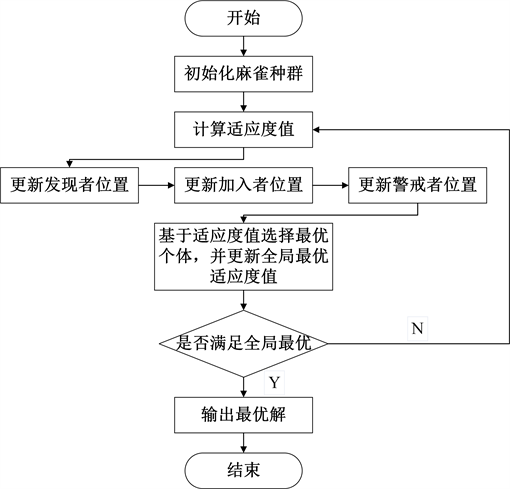
Figure 2. Flow chart of the SSA algorithm

图2. SSA算法流程图

3.3. SSA-GRU模型

本文利用SSA寻优算法优化GRU的超参数，把隐含层节点数、学习率和迭代次数看作待优化值，利用迭代取得最优解，避免超参数选择的经验性和随机性，实现GRU模型的精细化调参，提高模型的预测性能。构建模型的预测流程如图3所示。

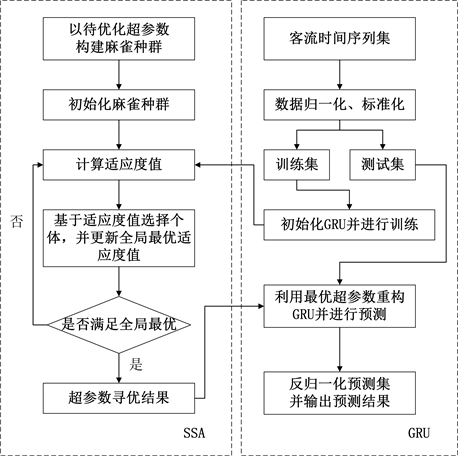
Figure 3. Overall architecture of the SSA-GRU model

图3. SSA-GRU模型整体架构

综上，SSA-GRU模型的预测过程如下：

Step1：初始化。确定GRU模型待优化参数，设置麻雀种群数量、最大迭代次数，种群中发现者与警戒者数量等；对客流数据集进行归一化处理，构建测试集与训练集，采用训练集对GRU模型展开训练。

Step2：随机给定预警值，并将预警值与安全值进行比较，利用式(9)更新发现者的位置。

Step3：利用式(10)更新加入者的位置。

Step4：利用式(11)更新警戒者的位置。

Step5：计算适应度值。选择GRU模型的预测值和样本数据的均方误差作为麻雀个体的适应度值，更新并保留最佳的适应度值及最优位置信息。

Step6：判断是否达到最优适应度值，若未达到重复执行步骤(3)，若满足条件则终止循环，输出最优超参数组合，并根据最优参数建立最优评估模型。

Step7：输出预测结果。基于超参数最优组合，利用GRU模型提取历史客流数据的时序特征进行短时客流预测，输出GRU模型最优的预测结果，并对模型预测结果进行评价。

4. 实验分析

4.1. 数据集及数据预处理

本文选取某市2022年9月1日到9月30日的公交站点客流数据作为样本数据进行实验，选择7:00~19:00作为采集实验数据的时间段，以30 min为时间粒度统计公交客流；根据实验将前70%的数据划为训练集，后30%的数据划分为测试集。

采用premnmx (mapminmax)函数归一化处理样本数据，加快模型的收敛速度与泛化能力，使输入的样本数值处于[0,1]之间。具体公式如下：

$Y_i=\frac{x_i-x_{\max }}{x_{\max }-x_{\min }},i=1,2,3,\cdots ,N$ (12)

式中： $x_i$ 为原始样本数据； $Y_i$ 是归一化后的数据； $x_{\max }$ 代表输入样本中的最大值； $x_{\min }$ 为输入样本的最小值。

对输出结果反归一化处理，使得最终输出的数据能够真实反应预测值，其公式如下：

$y_i=Y_i\left(x_{\max }-x_{\min }\right)+x_{\min },i=1,2,3,\cdots ,N$ (13)

式中： $Y_i$ 代表反归一化处理前的输出数据， $y_i$ 代表反归一化处理后的输出结果。

4.2. 评价指标

本文采用平均相对百分误差(MAPE)、平均绝对误差(MAE)与均方根误差(RMSE)作为评价指标评估模型预测性能。MAPE可以反映预测值的离散程度；MAE指各次测量值绝对偏差的平均值，反映预测值误差的实际情况；RMSE可以衡量预测值与实际值间的偏差，其值越小，模型的预测精度越高。三种公式如下：

$\text{MAPE}=\frac{1}{n}{\displaystyle {\sum }_{n=1}^n\left|\frac{x_i-y_i}{x_i}\right|}$ (14)

$\text{MAE}=\frac{1}{n}{\displaystyle {\sum }_{n=1}^n\left|x_i-y_i\right|}$ (15)

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle {\sum }_{n=1}^n{\left(x_i-y_i\right)}^2}}$ (16)

式中： $x_i$ 表示预测值的实际大小， $y_i$ 为预测值，n代表测试集的样本数量。

4.3. 模型实施及结果分析

本文模型实施基于DELL计算机(Intel(R) Core(TM) i5-6300HQ CPU，12G RAM)，在Matlab2020b环境中完成模型搭建和训练。首先，初始化GRU模型的超参数：两个隐含层的节点个数128、最大训练次数400、学习率0.001等，利用GRU模型进行短时客流预测，预测结果如图4所示。

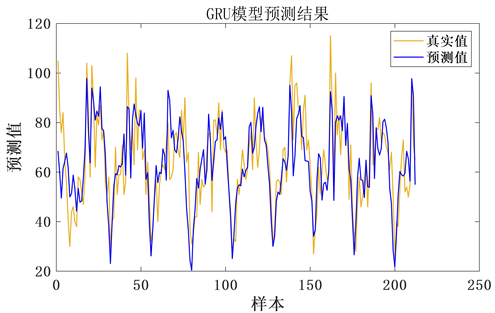
Figure 4. Prediction results of GRU mode

图4. GRU模型预测结果

其次，采用SSA优化算法进行超参数寻优。初始化SSA算法的参数值：种群规模为8、种群中麻雀发现者的数量占比为0.2、最大迭代次数400，分别对两个GRU隐含层节点个数(L1、L2)、训练次数(K)与学习率(lr)进行超参数寻优。参数迭代过程如图5所示，当SSA优化算法迭代至5次时趋于稳定，最优个体适应度大小稳定在0.0028，得到最优超参数组合；优化得到的GRU参数，可知学习率约为0.0063，两个隐含层节点数分别为37、42，训练次数为48。

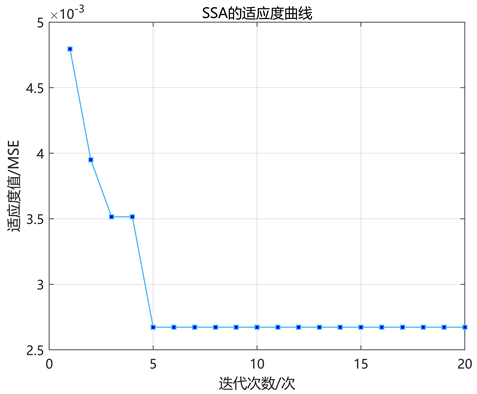
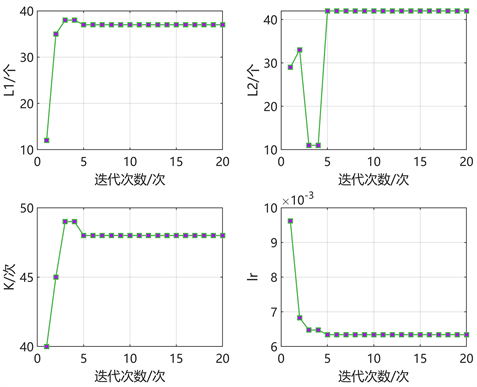
Figure 5. Iteration of SSA parameter optimization

图5. SSA参数寻优迭代

最后，基于超参数寻优结果进行短时客流预测。图6为SSA-GRU与GRU预测结果对比，由图6可知，SSA-GRU模型的拟合曲线与客流真实值曲线吻合度更高，这是由于SSA优化算法寻优的模型超参数与网络结构的匹配度更高，从而提高了模型预测精度。为便于清晰对比两种模型的预测结果。对预测结果进行量化处理，结果如表1所示。

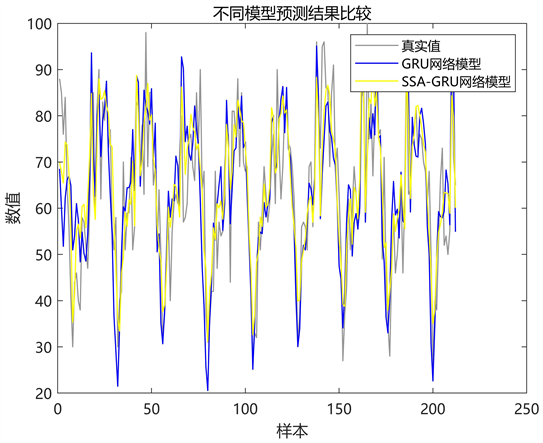
Figure 6. Comparison of prediction results of different models

图6. 不同模型的预测结果对比

Table 1. Comparison of prediction results of different models

表1. 不同模型的预测结果对比

模型优化前后的预测结果如表1所示，SSA-GRU模型预测结果与基础GRU模型相比平均相对误差降低了37.9%，均方根误差降低了40.7%，平均绝对误差降低了42.1%，结果表明，SSA-GRU模型在短时客流预测时的预测精度更高；采用SSA优化算法可有效对GRU模型中的超参数组合进行寻优，实现超参数的优化，进而提升模型的预测精度。

5. 结语

本文针对公交短时客流预测日趋精细化的需求，提出了一种基于深度学习优化(SSA-GRU)的短时客流预测模型，该模型利用GRU的非线性拟合能力以及深度学习能力挖掘短时客流的时序特征，克服原始客流数据非线性特征难以捕捉的问题；并通过引入SSA优化算法对GRU模型的超参数组合进行优化，有效避免GRU模型在超参数选择上的经验性与主观性。实验结果表明SSA-GRU模型的平均相对误差、均方根误差、平均绝对误差相分别降低了37.9%、40.7%、42.1%，均优于GRU模型，证明本文提出的预测模型拥有较高的优化效果，可以提升短时客流的预测精度。

基金项目

全国统计科学研究项目(2021LY017)；山东省自然科学基金项目(ZR2021MF019)；山东省自然科学基金项目(ZR2021QF110)。

NOTES

^*通讯作者。