山东省城市经济韧性实证研究——基于TOPSIS-AISM模型

Empirical Study on Urban Economic Resilience in Shandong Province—Based on the TOPSIS-AISM Model

摘要: 党的二十大报告强调，坚持把发展经济的着力点放在实体经济上。作为实体经济大省，山东纵深推进新旧动能转换，着力构建现代化产业体系。而区域经济韧性作为山东省经济发展的软实力，其定性测度还未有学者着墨。本文以山东省16地市作为实证分析的对象，从鲁棒性、冗余度、效率度与再组织力四方面作为切入点，采用TOPSIS与AISM模型的结合方法，构建了指标体系并探究了山东省16地市经济韧性的强弱程度。相较于传统的解释结构模型，AISM模型有效保证了系统功能并得出最简化的层次化拓扑图，将评价结果直观展示出来。研究发现，山东省各地市的经济韧性强弱与各地市经济发展情况基本吻合，而在指标体系中，鲁棒性与再组织力对城市经济的强弱有着重要的支撑作用。

Abstract: The report of the Party’s 20th National Congress stressed that the focus of economic development should be placed on the real economy. As a province with a large real economy, Shandong has deeply promoted the transformation of old and new growth drivers and focused on building a modern industrial system. However, as the soft power of Shandong Province’s economic development, the qualitative measurement of regional economic resilience has not been studied by scholars. Taking 16 municipalities in Shandong province as the object of empirical analysis, this paper has combined TOPSIS and AISM model to establish an indicator system and investigate the strength and weakness of the economic resilience of 16 municipalities in Shandong Province from four aspects: robustness, redundancy, efficiency and reorganization force. Compared with traditional interpretation structure models, the AISM model effectively guarantees system func-tionality and produces the most simplified hierarchical topology diagram, displaying evaluation results. It is found that the strength of economic resilience of cities in Shandong Province is basically consistent with the economic development of cities, and in the index system, robustness and reorganization have important supporting roles for the strength of urban economy.

1. 引言

城市作为复杂巨系统，是经济、政治、文化等活动的中心平台。然而，随着城镇化的提升，城市也面临着诸如金融风险、极端天气、重大公共卫生事件等外部扰动。所以，这些外部扰动与安全风险倒逼着“智慧、宜居且富有韧性”的城市系统建设。其中，经济韧性指城市在遭受经济风险时，能够抵御危机、减轻危机并合理高效调配资源并恢复至原有经济水平的能力。城市经济韧性的强弱不仅直接影响到经济高质量发展与金融系统稳定，还与人民福祉息息相关。山东省作为人口大省、经济大省与农业大省，是全球唯一的41个制造业大类都齐全的省份，其经济总量相当于全球第18的经济体，是中国经济的“压舱石”。然而，学者们对山东省城市经济韧性的实证研究还着墨不多。本文通过构建鲁棒性、冗余度、效率度与再组织力四个二级指标，选取2021年山东省各地市的全社会消费品总额比重、产业结构高级化水平等27个三级指标，通过TOPSIS-AISM结合的方法全面、系统地对其经济韧性的测度，并给出了相关结论。

2. 城市韧性与城市经济韧性

2.1. 城市韧性

韧性的概念经历了工程韧性、生态韧性再到演进韧性的变迁。韧性一词最早出现于工程学领域，指物体在遭受外部压力时，能够恢复其形变的能力。工程韧性的观点是当时的韧性理念的主流观点，即系统只有单一稳态。1973年，霍林 [1] 将这一概念引入至生态学领域，以衡量单一生态系统经历扰动时的稳定能力。但在20世纪80年代，随着学者们对于系统作用机制理解的深入，认为系统可以有多个稳定状态。霍林认为，韧性理念的内涵应当包含系统在改变自身的结构之前能够吸收的扰动量级。随后，学者们普遍认同在经历外部扰动后，系统不仅存在恢复到原有稳定水平的单一可能性，也有可能达成更高或更低的稳态，即为生态韧性。在此基础上，沃克 [2] 将变化(change)、适应(adapt)与改变(transform)的理念引进到这一框架中，抛弃了传统意义上“稳态”的概念，而强调了系统持续不断地适应的能力，即韧性应为一种动态的系统属性。2001年，刚德森与霍林 [3] 共同提出了“适应性循环理论”，认为单一系统应经历利用(exploitation)、保存(conservation)、释放(release)以及重组四大阶段(reorganization)。某种程度上而言，适应性循环理论阐明了系统恢复能力或韧性的深刻内涵，但未能对系统恢复力的阈值进行定性测量。究其根本，阈值的测定方法难以找出稳定的可替代性状态与显著的关键性控制变量这两个必要条件，所以，现阶段对于测量方法的研究还有待探索。

在全球经济危机、重大安全事件与气候变化等诸多城市安全隐患增加的大背景下，韧性理念在工程学、社会学与生态学领域的广泛应用也启发了城市规划、城市治理等领域的学者。当前，对于城市韧性主流的定义为在城市遭受外部扰动时，能够抵御、恢复乃至提高的能力。学者们对于城市韧性的定义有三大相同点，首先，城市系统应具有多元性。城市系统的多元性不仅体现在城市具有为人类开展各种必要的生产生活条件等功能性的多元化，还体现在当城市遭受外部扰动时选择的多元性。其次，城市系统也应具有高度的自组织能力，即当遭受外部扰动时，城市系统通过合理统筹规划物资分配、人员调动来应对灾害的能力。最后，城市要有足够的冗余度。冗余度指的是城市要储备一定的功能性和备用设施，以在时间与空间格局上淡化外部扰动对城市功能性上的冲击。

2.2. 城市经济韧性

在城市韧性理念的基础上，又可延伸出城市经济韧性、城市医疗韧性、城市交通韧性多种子领域概念。城市经济韧性的概念发展大致可分为两个阶段：第一阶段启蒙期(2003~2010年)，学者们试图将相关理论与空间经济学、空间测量学领域学科基础进行联系；第二阶段概念成熟期(2011~现在)。Boschma (2014) [4] 认为，经济韧性应当内化为城市或区域抵御外部扰动的长期核心能力。随后，Sunley (2015) [5] 等提出脆弱性、抵抗性、重定向力与恢复能力四者之间的关系是联系的而非割裂的，共同组成了经济韧性的适应调整性能力。2016年后，经济韧性的测度与评价方法硕果累累。从国家层面，Sensier (2016) [6] 及其科研团队测算了欧洲31个国家的经济韧性。Faggian (2017) [7] 通过失业人口数量的变化率对意大利测算了其经济韧性。与此同时，Fingleton (2017) [8] 利用反事实预测，构建空间面板模型，探究了经济产出与就业水平的因果关系，衡量了美国大都市区的经济韧性。至于国内的实证研究，刘晓星(2021) [9] 采用风险吸收强度和吸收持续期定量测度了中国的宏观经济，对实现新发展格局的理论探索具有重大意义。张安伟和胡艳(2023) [10] 从多中心空间结构入手，为推动产业结构转型升级以及建设具有韧性的城市提供了政策参考。

综上所述，中外学者为城市韧性理论与区域经济韧性测度做出了重要积累，但对国内的单个城市与对城市群经济韧性测度的实证案例还不多。与此同时，目前的研究中也忽略了对于背后驱动机制的探究。本文认为，城市韧性源于实现社会整体效益最优的统筹智慧，故将城市经济韧性定义为城市在遭受外部扰动时，能够在保持原有功能性不变的基础上，能最大限度维持经济系统稳定性的能力。

3. 指标选取与研究方法

3.1. 指标选取与数据处理

指标选取

考虑到现有城市韧性研究指标体系的科学性，并考虑到山东省16地市实际，将从鲁棒性(robustness)、冗余度(redundancy)、效率性(efficiency)与适应度(fitness)四方面构建医疗韧性评价指标体系，如表1。

Table 1. The meaning and attributes of robustness, redundancy, efficiency, and fitness

表1. 鲁棒性、冗余度、效率度与适应度的含义与属性

首先，在鲁棒性指标中，本研究选取了人均生产总值等9项三级指标。人均生产总值、居民人均可支配收入、居民储蓄存款余额体现了整体居民的个人收入能力，还反应了其风险抵抗能力。第一产业比例、贸易水平、GDP增长率与城镇化率等指标分别反映了区域内一产发展水平 [11] ，对外经济开放程度与城镇化水平。恩格尔系数指食品支出占总消费的比重，该指标随着生活的富裕应逐步降低，为负向指标；其次，冗余度指的是城市要储备一定的功能性和备用设施，以在时间与空间格局上淡化外部扰动对城市功能性上的冲击 [12] 。人口自然增长率与就业自然增长率分别反映了该区域内人口与就业发展的情况，第二、第三产业贡献度反映了第二产业与第三产业的发展水平。财政水平主要指财政的自给水平，其计算口径为该地区的一般预算收入与地方财政一般预算支出之比。而全社会消费品零售总额比重反映了消费拉动经济增长的水平，二者均用以衡量该地区的社会恢复环境 [13] ；再次，效率度选取了6项三级指标。其中，高等学校数量、每千人卫生医疗机构人数从高等教育与医疗 [14] 两方面补充了经济韧性的社会保障能力，高校的兴衰客观决定了城市的智慧化高低与就业人口的数量与素质，而充足的医疗卫生基础服务设施与经济水平对城市医疗韧性有着稳定作用。产业结构高级化水平的计算口径为“第一产业占比 * 1 + 第一产业占比 * 2 + 第三产业占比 * 3”，反映了三种产业类型阶梯程度与合理度。金融水平则采取了金融机构存贷款余额之比；最后，再组织力反映了城市经济韧性的适应、学习与提高的能力。其中，区域的收入与消费协调水平均采用该城市与全省平均收入与消费之比的方式来测度。城乡二元的概念源于我国采用的割裂的城乡管理的体制，随着我国乡村振兴的深入实施，城乡二元的差距越来越小。城乡二元差距的计算口径城镇居民人均可支配收入(消费)比农村居民人均可支配收入(消费)之比，该指标为负向指标，各项三级指标体系如表2所示。

Table 2. Index system

表2. 指标体系

3.2. 数据来源

本研究的所有原始数据来源均取自于《山东省统计年鉴2022》与山东省各地市的2022年统计年鉴，此类年鉴详细记录了2021年山东省及各地市的人民生活、人口、经济社会发展、工业等数据。其中，人均地区生产总值、居民可支配收入等指标直接可查，而公共管理、社会保障和就业比重、产业结构高级化水平、城乡二元收入差距等指标在原始数据的基础上进行了简单运算后得出。

4. 模型建立

4.1. TOPSIS模型

逼近理想解排序法(Technique for Order Preference by Similarity to an Ideal Solution，简称为TOPSIS法)由C. L. Hwang和K. YOON提出，是一种经典的综合评价法。TOPSIS法对于各个评价对象进行赋权，根据各个属性值距各评价方案的最好与最坏情况分为了正负理想解，以精确地评判出各评价方案的差距。同时，TOPSIS法结合欧氏距离法，将各指标与最佳解和最劣解进行距离排序。若该欧式距离满足距最优解最近且离最劣解最远，则为最优，则该方案为最佳的备选方案；反之，则为最差的备选方案。

4.1.1. 计算正、负理想解(d⁺、d⁻)

到正向理想解的距离：

$d^{+}=\sqrt{{\displaystyle {\sum }_{j=1}^m{\left(c_j^{+}-c_{ij}\right)}^2}}$ (1)

到负向理想解的距离：

$d^{-}=\sqrt{{\displaystyle {\sum }_{j=1}^m{\left(c_{ij}-c_j^{+}\right)}^2}}$ (2)

4.1.2. 计算相对贴近度

$C=\frac{D_i^{-}}{D_i^{-}+D_i^{+}}$ (3)

4.2. AISM模型

对抗解释结构模型(Adversarial Interpretive Structure Modeling Method，简称为AISM模型)衍生于解释结构模型(ISM)。相较于传统的ISM模型，AISM加入了对抗与博弈的思想，更加关注处于不同层级的要素。一言以蔽之，传统的ISM模型依据帕累托最优的层级抽取规则只以结果作为优先级，抽取规则为 $R_{\left(e_i\right)}=T_{\left(e_i\right)}$ ，当可达集合与共同集合相一致时，由上至下地放置抽取的元素，直接提取系统中最终结果的元素。是一种结果优先的抽取方法。而AISM模型在此基础上依据帕累托最劣的原则，以原因优先的方式建立了对抗关系，抽取规则为 $Q_{\left(e_i\right)}=T_{\left(e_i\right)}$ ，即为先行集合与共同集合相一致时，由下至上放置抽取的元素，提取系统中最终原因的元素。

因此，通过建立两组有向拓扑图，对山东省16地市的经济韧性进行综合比较，能更加有效地探索其内在联系与排序情况。其计算过程如下：

$A\stackrel{A+I}{\to }B\stackrel{可达矩阵}{\to }R\stackrel{对立层级抽取}{\to }\left\{\text{UP}|\text{DOWN}\right\}\stackrel{带入S}{\to }对立的层级有向拓扑图$

其中：A为原始布尔关系矩阵；B为加入单位矩阵后(B = A + I)相乘矩阵；R为可达矩阵；S为一般性骨架矩阵；{UP/DOWN}为一组对抗型拓扑有向图。

4.2.1. 依据偏序规则得出关系矩阵

在决策矩阵D中，若有n列，则有n个不同指标维度。其中，将正向指标记为 $u_1,u_2,u_3,\cdots u_n$ ；将负向指标记为 $v_1,v_2,v_3,\cdots v_n$ 。对于矩阵D中的任意两行x与y，应满足：

负向指标： $d_{\left(x,u1\right)}\ge d_{\left(y,u1\right)}$ 且 $d_{\left(x,u2\right)}\ge d_{\left(y,u2\right)}$ 且 $\cdots d_{\left(x,un\right)}\ge d_{\left(y,un\right)}$ ，

正向指标： $d_{\left(x,v1\right)}\le d_{\left(y,v1\right)}$ 且 $d_{\left(x,v2\right)}\le d_{\left(y,v2\right)}$ 且 $\cdots d_{\left(x,vn\right)}\le d_{\left(y,vn\right)}$ 。

要素x与y的偏序关系记为 $x<y$ ，意为y要素优于x要素。决策矩阵D通过偏序关系可得到关系矩阵A。其中，若 $x<y$ ，记为0；若x与y无完全优劣关系或 $x>y$ ，则记为1。

$a_{xy}=\{\begin{array}{l}0,x<y\hfill \\ 1,x与y无完全优劣关系或x>y\hfill \end{array}$ (4)

4.2.2. 建立可达矩阵

可达矩阵指的是用矩阵形式来描述图的各节点之间经过一定长度的通路后可达到的程度。山东省各市经济韧性的可达矩阵是在关系矩阵A的基础上加单位矩阵I，可达矩阵R的计算方法如式(5)与式(6)所示：

$B=A+I$ (5)

$B^k=B^{k+1}=R$ (6)

其中，B为相乘矩阵，即对角线上的元素都加1；I为0~1矩阵；R为可达矩阵，不难得出R = A。

4.2.3. 运算骨架矩阵

由可达矩阵进行缩点即把可达矩阵中的回路当成一个点，称之为缩点。缩点后进行缩边运算，即为其删除重复的路径：

$S=HS=R-{\left(R-I\right)}^2-I$ (7)

其中，S为骨架矩阵，HS为哈斯矩阵。

4.2.4. 层级抽取

对于可达矩阵，有先行集合Q、可达集合R、共同集合T，其中T为R与Q的交集，即为 $T=R\cap Q$ 。例如， $Q_{\left(e_i\right)}$ 为元素 $e_i$ 的先行集合， $R_{\left(e_i\right)}$ 为元素 $e_i$ 的先行集合。二者分别对应在列上与行上所对应的所有要素。故 $T_{\left(e_i\right)}$ 为元素 $e_i$ 的共同集合。其中：

(1) UP型层级图(由果索因)为以结果优先的层级抽取，规则为 $R_{\left(e_i\right)}=T_{\left(e_i\right)}$ ，由上至下地排布山东省16地市的样本，以此类推。

(2) DOWN型层级图(由因索果)为以原因优先的层级抽取，规则为 $Q_{\left(e_i\right)}=T_{\left(e_i\right)}$ ，由下至上地放置样本。UP型层级图与DOWN型层级图互为对立关系，帕累托最优的样本置于最上级，反之帕累托最劣的样本则处于最下级。

4.3. TOPSIS-AISM模型

AISM模型有效充实了TOPSIS法的研究内涵，将其直链形式的排序结果动态化，变化为具有跳跃性质的排序结果。二者的结合，将山东省16地市的韧性水平进行测度，再分层抽取，把静态的模型动态化，立体展示其分析整体夹逼的过程，将各市的医疗韧性水平划分得更加清晰。通过给出UP型与DOWN型有向层级拓扑图综合比较，增加了结果的可信度。

5. 实证分析

5.1. TOPSIS求解

在构建决策矩阵后，通过TOPSIS模型计算得出各项三级指标的权重，如表3所示。

Table 3. The weights of various urban economic resilience indicators

表3. 各项城市经济韧性指标的权重

随后，可计算出各个城市的正负理想解d⁺、d⁻与贴近度C_i。如表4所示。

Table 4. Positive and negative ideal solutions and closeness

表4. 正负理想解与贴近度

取山东省16地市的贴近度C_i为基准，取贴近度在0.55以上的城市为“强”韧性，贴近度在0.49至0.54的城市为“较强”，贴近度在0.41~0.49的城市为“中等”韧性，而介于0.35至0.40的城市为“较弱”，如表5所示。

Table 5. Classification of urban economic resilience in 16 cities in Shandong Province

表5. 山东省16地市经济韧性等级划分

通过表3可知，结合熵值法，居民储蓄存款余额的权重为11.7%，从微观经济而言，该指标体现了区域内居民的风险的抗风险能力的同时也在宏观上体现了该地区的总体储蓄水平与拉动内需的潜力。济南市与青岛市的居民在2021年分别存款余额为23,437元与22,374元，济南与青岛作为山东省唯二的副省级城市，无论是在国家政策还是城市基础设施上都要明显优于其他的城市，更高的城市政治级别与优越的营商环境也在客观上为居民更富足的生活打下了基础。信息传输、软件和信息技术服务人员的重要性为11.07%。在新兴信息技术与传统产业不断加深的背景下，工业、互联网与制造业的人才会为城市经济发展注入新动能。山东省作为全国新旧动能转换综合试验区，新一代信息技术在经济社会各领域开展广泛应用和模式创新，支撑制造业、农业、金融、能源、物流等传统产业优化升级，为传统产业“赋智赋能”；特别是在工业领域的应用加快，2018年，工业软件收入增长14.2%，工业互联网正在成为新一轮工业革命和产业变革的焦点；支持智慧城市、智慧交通、智慧社区、智慧医疗等建设，帮助解决社会管理和民生问题的同时，创造出新的市场需求。全员劳动生产率占据了10.28%的权重，该指标的计算口径为国内生产总值与年平均从业人员数量的比值，山东省各地市间全员劳动生产率差异较大，且全员劳动生产率较高区域分布比较集中。高于全省一般水平的东营、青岛、济南、烟台、威海和淄博六市，主要集中于省会经济圈和半岛城市群，低于全省一般水平的城市多分布在鲁西北和鲁南地区，基本与山东省经济发展的区域差异一致。直观体现的热力图由图1所示。

5.2. AISM求解

5.2.1. 计算关系矩阵A与建立可达矩阵R

由表4中计算出的正负理想解d⁺、d⁻组成的决策矩阵，可以进一步算出关系矩阵 $A={\left(a\right)}_{16\times 16}$ 。随后，再结合公式(5)与(6)经布尔运算后，可计算出可达矩阵R。如表6所示。

5.2.2. 计算并绘制UP型有向拓扑图与DOWN型有向拓扑图

通过计算出山东省16地市的可达集合R与先行集合Q，取T为二者的交集。随后，可根据抽取规则，分别逐级抽取UP型和DOWN型拓扑层级后，抽取过程见表7。

随后，可得出对抗层级抽取结果，要素分层如表8所示。

根据表8，即可绘制出UP型与DOWN型层级图(如图2所示)。

第一，通过AISM模型的降维结果来看，山东省16地市的样本优劣清晰可见。经图2的UP型与DOWN型对抗层级拓扑图可视化比较，二者的划分层级基本一致。依据上层表现更优，下层表现更差的原则，山东省各地市的经济韧性共分为9个层级，韧性水平依次递减。即L0级的青岛市是医疗韧性最强

注：该图给予自然资源部标准底图服务网下载的审图号为GS(2019)1882号，底图无修改。

Figure 1. Proximity heat maps of 16 cities in Shandong Province

图1. 山东省16地市经济韧性贴近度热力图

Table 6. Relation matrixA

表6. 关系矩阵A

Table 7. SetsR, Sets Q and their intersection tableT

表7. 可达集合R与先行集合Q以及其交集T

Table 8. Element stratification

表8.要素分层

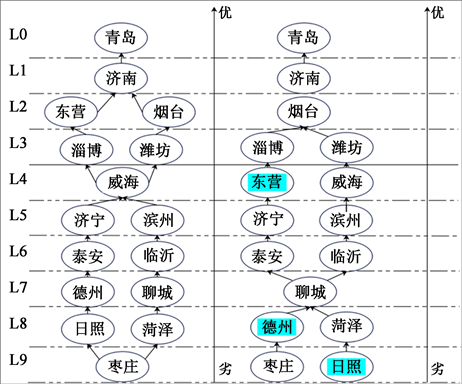
Figure 2. The UP and DOWN adversarial hierarchy topology

图2. UP型对抗层级拓扑图与DOWN型对抗层级拓扑图

的城市而L9级的枣庄市与日照市为经济韧性程度最薄弱的城市。其中，东营市横跨两个层级，而德州市与日照市均横跨一个层级，三者皆属于活动要素。

第二，鲁棒性对于经济韧性的高低具有强支撑作用。结合指标权重与层级拓扑图来看，居民储蓄存款余额、可支配收入越高，城市的经济实力就越强。同时，城镇化率与城镇失业保险人数等指标增强了城市的经济刚性，也对人民生活幸福感和保障有着巨大支撑作用。纵观拓扑层级图，经济韧性较强的省份有青岛、济南与烟台，这三座城市本身就长期位列山东省国民生产总值前三甲，其企业实力、科技创新能力、政策利好与地理位置等方面让其他城市望其项背。而经济韧性较弱的城市有枣庄、德州、菏泽与日照等城市，这些城市多位于鲁西或鲁南地区。枣庄原本以煤炭立市，但随着资源日益枯竭与新旧动能转换的双重叠加，枣庄市经济增长乏力。德州与日照两城虽位于不同的经济圈，但德州紧邻省会济南，日照紧邻青岛，加以两地在高铁网络与对外沿海方面的便利性，加剧了其被大城市的虹吸效应，造成人才与资源的流失。菏泽市自然资源相对匮乏，人口结构主要以农业为主。可喜的是，菏泽市在近三年的主要经济指标进步明显，但很多成绩的背后离不开人口的红利。

6. 结语

测评城市经济韧性是加快新旧动能转换、落实“六稳”“六保”工作中的重要前置关口。本文从鲁棒性、冗余度、效率度和再组织力四个方面构建了27个指标综合测评了山东省16地市的经济韧性。通过TOPSIS-AISM模型立体展示了优劣排名。主要结论如下：

第一，从空间格局上看，山东省整体呈现“东强西弱”的格局，山东省各地市的经济韧性格局与经济水平大致相符。济南与青岛两座副省级城市当之无愧占据第前二位，胶东经济圈整体韧性较强；省会经济圈中的城市除德州与泰安较弱之外，其余城市韧性中等；鲁南经济圈经济韧性偏弱，仅有临沂与济宁两座城市经济韧性较强。

第二，从指标体系来看，鲁棒性与再组织力的强弱对经济韧性强弱有较强影响。值得一提的是，再组织力是实现创新的重要抓手，有了强大的经济社会发展创新力，服务和融入新发展格局就有了充沛动力和活力，也高质量发展的坚实基础和支撑。

在全国34个省级行政区中，山东省的经济水平一直稳居前三甲。山东省近年来财政运行保障有力，卫生、住房、教育等与人民福祉有关的经济指标支出增长较快；同时，山东省金融市场运行稳健，资本市场更加活跃。“省会”、“胶东”与“鲁南”经济圈区域经济韧性发展协调，实现地区生产总值分别为32,637.0亿元、37,458.0亿元和17,339.8亿元，按不变价格计算，比上年分别增长3.8%、3.9%和4.3%，对全省经济增长的贡献率分别为36.6%、42.0%和21.4%，三大经济圈的经济韧性基本与其经济发展水平相符。