1. 引言
仿真技术现已广泛地应用于电力工程研究领域,在电力系统分析、运行与控制中扮演了越来越重要的角色。新型电力系统的建设呈现高比例新能源、高比例电力电子设备的“双高”特性,电力系统稳定形态和运行特点发生深刻改变,动态响应时间尺度从毫秒向微秒级发展,对电力系统仿真技术提出了更高的要求。传统的机电暂态仿真难以满足支撑新形势下的仿真计算需求,而全电磁暂态仿真作为目前最详细、精确的仿真手段,对电网规划方案论证、控制策略优化、新技术应用等具有十分重要的意义,为新型电力系统构建保驾护航 [1] [2] [3] 。而仿真精度问题一直是专家和系统分析人员所关注的,能否根据仿真数据和实测结果,给出具体量化指标,从而为模型和参数的修正提供依据以达到提高仿真精度的目的,这一问题亟待解决 [4] 。
提高电力系统全电磁暂态数字仿真模型精度的首要工作是给出具体的仿真精度的量化指标。仿真精度评估的实质是对比实测数据与仿真数据的相似度。最初的相似度评估方法是通过肉眼观察实测数据与仿真数据给出结论的定性分析,目前已有了图示法等一些改进的更加直观的定性分析方法。而相似度的定量评估不仅要求给出的评估结果准确合理,而且应能为提高仿真精度提供必要的信息和参考意见。文献 [5] [6] 提出了借助相似度具体量化仿真系统可信度的方法,并结合实例阐明了这种方法的工程应用;文献 [7] 提出了利用相似度理论和层次分析法进行电力系统动态仿真的有效性验证。文献 [8] 应用频谱分析方法进行仿真可信性评估,引入瞬时谱估计分析非平稳随机信号;文献 [9] 使用Prony变换提取曲线各特征量、使用频率相似度和阻尼相似度表征误差,由于Prony方法不适用于分析强非线性曲线,而电力系统在发生故障时却表现为强非线性,所以该方法具有一定局限性。上述几种方法在计算相似度时考虑的只是数据序列的静态的数值接近程度,而没有从动态角度考虑曲线变化趋势的相似程度 [10] [11] 。本文提出了评估仿真精度的两个重要指标:残差相似度与形状相似度,提出了一种能从静态和动态两个方面综合考虑曲线相似程度的评估方法,并结合2020年华东“9∙27”故障下±1100 kV昌吉–古泉特高压直流输电系统的实测和仿真数据进行了仿真精度评估。
2. 仿真精度量化指标的计算
2.1. 残差相似度
曲线残差相似度计算的主要思路为,将实测数据的比较时间序列减去仿真数据序列,利用曲线之间的距离来衡量曲线的相似性。目前计算两个时间序列的残差相似度计算主要是:基于序列间的点距离方法或其改进方法,常用的距离函数有明可夫斯基距离、欧氏距离等。本文采用平均百分比误差来比较两个数据序列的静态度量差异,其本质就是采用直接距离法比较曲线间的数值接近情况,这样就可以简单直观的给出两条曲线间的残差相似度结果。具体的计算公式如(1)所示。
(1)
式中,n表示数据序列的采样点数,
表示实测数据序列第i个点的采样值,
表示仿真数据序列第i个点的采样值,
表示实测数据序列
与仿真数据序列
之间的残差相似度。
利用平均百分比误差来计算曲线的残差相似度的方法优点是简单直观,计算复杂度不高。但该方法用于比较以曲线的“变化趋势”为关注重点的时间序列时存在本质的缺点,因为点距离是一种静态的度量方法,无法有效的体现时间序列的动态特性,而评估仿真结果时仍需要综合考虑曲线的静态和动态两方面因素,所以该相似度计算方法应与后面的形状相似度结合以给出仿真精度的综合评价指标。
2.2. 形状相似度
曲线形状相似度计算的实质是反映两条曲线变化趋势的相似情况。该方法在计算机模式识别、数据挖掘等方面应用广泛,已有的方法包括界标分界法、时间弯曲模型法等。标准系数法是目前评估时间序列形状相似度的一个快速有效的方法 [12] [13] 。该方法的主要思路是充分考虑了时间序列的噪声、幅度、偏移等问题,认为如果两个时间序列有足够多的不相互重叠,按时间顺序排列且相似的原子序列,则这两个序列相似。下面详细介绍使用标准系数法进行曲线形状相似度计算的过程。
首先是采用宽度为
的滑动窗口将数据序列划分成n个原子序列,保证使每个原子序列的宽度相等,然后对每个原子序列
先按下式进行偏移变化和幅度缩放:
(2)
其中
为原子序列中的第i个序列元素,
、
分别是原子序列中的最大、最小元素,
为变换后的序列元素,显然它是界于[−1,+1]之间。对于两个数据序列中对应的原子序列
,
,
,
(
为人为给定的相似阈值)则称两个原子序列是趋势相似,并
用相似原子序列的长度与原数据序列长度的比值作为相似性的度量,即:
(3)
式中,
、
分别为数据序列Y、
的第i个相似的原子序列,k为相似子序列的个数,
表示实测数据序列y与仿真数据序列
之间的形状相似度。该方法通过标准变换消除了水平偏移、幅度伸缩以及部分噪声对相似性的影响,能有效比较两条曲线的变化趋势。该方法在计算机数据挖掘中应用广泛。
3. 仿真精度的综合评估
在评估仿真精度时,我们不仅要关心仿真曲线与实测曲线在距离上的接近程度,同时也要考虑仿真结果的变化趋势能否与实际情况相符、能否准确反映系统的真实情况。本文提出了电力系统实时数字仿真精度的综合评估方法,不仅考虑了曲线间距离上的残差相似度,也考虑了曲线变化趋势的形状相似度。具体的计算公式如(4)所示。
(4)
其中,
代表了实测数据序列Y相对于仿真数据序列
的相似度,
和
分别为前文所给出的两个数据序列的残差相似度和形状相似度。参数
代表残差相似度的权重系数,体现
了评估者对残差相似度与形状相似度的偏重程度。
的大小由应用人员凭对曲线残差与变化趋势的关心程度来主观确定,通常
的取值为0.3~0.7。
越大,表示评估者越偏重于数据序列之间的距离误差。
对于仿真试验获得的数据序列,根据故障发生的不同阶段可以将其分为四个时间阶段:故障发生前的稳态、故障过程中的暂态、故障切除后的暂态及最后的稳态。系统分析人员对这四个时间段仿真结果的看重程度也不一样,通常更关心的是故障过程中及故障切除后的暂态过程。为在评估仿真精度时体现各个时间段的权重区别,在分别计算每段数据序列的相似度后给其计算结果赋予一个权重系数,求和后再计算出整条曲线的相似度。
(5)
式中,
为第j个时间段的权重系数,
为第j个时间段实测数据与仿真数据的相似度计算结果,
为两条曲线的仿真精度评估结果。
为合理体现每个时间段的仿真精度对整体评估的影响,确定权重系数
,本文采用层次分析法(analytic hierarchy process, AHP)进行计算 [5] 。
具体步骤如下:
1) 建立判断矩阵
(6)
式中,
表示Bi与Bj相比的相对重要程度,Bi表示第i个时间段。当Bi与Bj一样重要时
取1;当Bi比Bj稍重要时取3;当Bi比Bj重要时取5;当Bi比Bj重要得多时取7;当Bi比Bj极其重要时取9,
。
2) 计算各个时间段权重值
对判断矩阵B求满足
的特征值与特征向量,其中
为B的最大特征值;
为对应
的正规化特征向量;
的第i个元素
即为第i个时间段的权重值
。
3) 判断矩阵一致性
使用矩阵的一致性指标CI与同阶次的平均随机一致性指标RI的比值CR来检验判断矩阵是否具有满意的一致性,RI为平均随机一致性指标,RI的计算方法为:用随机方法构造500个样本矩阵,随机的从
1~9及其倒数中抽取数字构造正互反矩阵,求得最大特征根的平均值
,并定义
,具体推
导方法见文献 [14] 。层次分析法中平均随机一致性指标RI如表1所示。

Table 1. Comparison table of average random consistency index RI
表1. 平均随机一致性指标RI对照表
4. 仿真试验与精度分析
为验证利用上述的仿真精度评估方法进行仿真波形与现场实测波形相似度比较时的有效性,本文基于ADPSS电力系统全数字实时仿真装置对2020年华东“9∙27”故障进行了故障反演仿真,结合±1100 kV昌吉–古泉特高压直流输电系统的现场实测数据及仿真计算结果,给予具体的实例说明。
4.1. 全电磁暂态数字仿真模型构建
2020年9月27日,华东电网东吴变电站,1000千伏线路泰吴线(东吴侧母线)发生单相接地故障,引起6回直流换相失败,造成了华东地区短时功率缺额近2700万kW。按照故障前的现场运行方式,在ADPSS系统全数字实时仿真装置上构建了华东区域电网全电磁暂态模型,如图1所示,包含10回直流输电系统,353台发电机,1748台马达,4735个交流三相母线节点。其中10回直流均接入实际控保装置,控保屏柜216面,数字仿真模型与控保屏柜的交互信号4890路。图1为构建的华东电网ADPSS全电磁暂态仿真模型。本案例采用具有384核心的2台国产高性能服务器,通过大电网电磁暂态仿真实时性综合平衡优化工具,解决CPU核的计算负载和通讯负载不均衡,实现全网50 us步长的实时仿真。

Figure 1. ADPSS full-electromagnetic transient simulation model of East China Power Grid
图1. 华东电网ADPSS全电磁暂态仿真模型
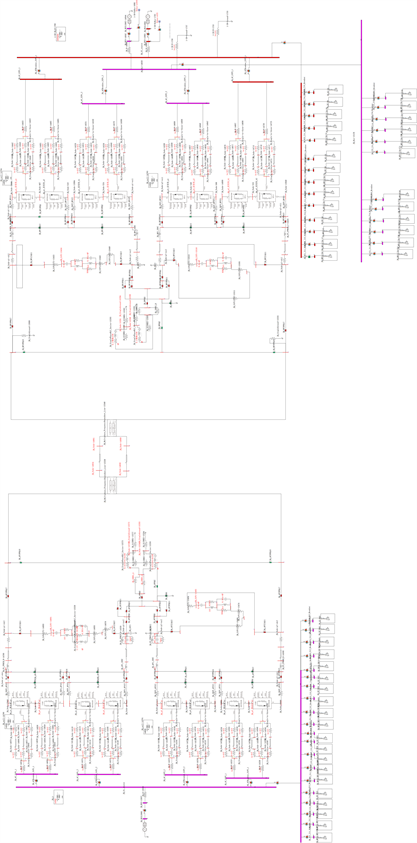
Figure 2. ADPSS full-electromagnetic transient simulation model of ±1100 kV Changji-Guquan UHVDC transmission system
图2. ±1100 kV昌吉–古泉特高压直流输电系统ADPSS电磁暂态仿真模型
以±1100 kV昌吉–古泉直流为例,结合上述仿真精度评估方法,进行电力系统全电磁暂态数字仿真模型精度评估,图2为±1100 kV昌吉–古泉特高压直流输电系统ADPSS电磁暂态仿真模型。其中昌吉站接入的交流系统采用电压源等值的方式,古泉站是分层结构,高低压阀组分别通过相连的换流母线与交流网连接,接入华东电网。
故障前吉泉直流双极运行功率为7140 MW,直流电压1100 kV,直流电流为3570 A。故障导致了古泉站双极低端阀组发生了换相失败,同时双极高端阀组所连接的交流母线电压也降低到0.9 pu附近,导致连接高端阀组单极发生了换相失败;古泉站直流母线电压降低到200 kV左右,直流电流的峰值到达了7000 A左右;故障消失后,直流电压、电流逐步恢复到故障前状态。古泉站极1直流电压、直流电流的仿真试验结果和实际录波对比如图3、图4所示,图中蓝色曲线代表仿真波形,黑色曲线代表现场实际录波波形。
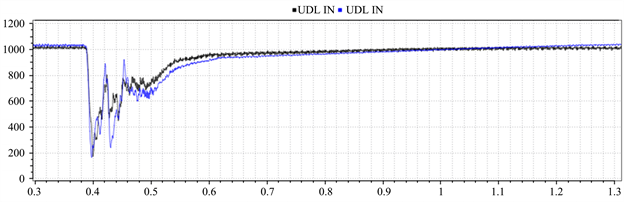
Figure 3. Comparison of field and simulation waveforms of pole 1 DC voltage at Guquan Station
图3. 古泉站极1直流电压现场与仿真波形对比图
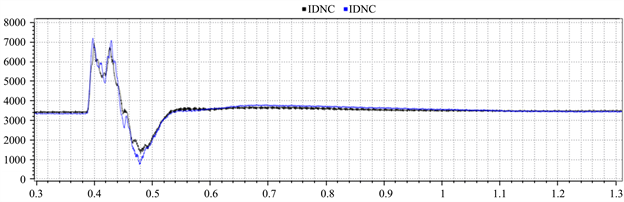
Figure 4. Comparison of field and simulation waveforms of pole 1 DC current at Guquan Station
图4. 古泉站极1直流电流现场与仿真波形对比图
由试验结果可看到,直流电压和直流电流的仿真波形与实际波形略有差异,不过曲线的基本形状及变化趋势都吻合的较好,说明通过仿真试验比较成功地再现了实际故障的全过程。但是要准确客观地评价仿真波形和实际波形的差异,从而给出仿真精度的具体量化指标,仅通过定性分析法是无法解决的。
4.2. 仿真精度分析
根据直流电压、直流电流的变化情况可以判断:0.3~0.38 s为故障发生前稳态(B1);0.38~0.48 s为故障过程中的暂态(B2);0.48~0.64 s为故障发生后的暂态(B3);0.64~1.3 s为故障切除后的稳态(B4)。在确定判断矩阵B的参数时,由于最关心的是暂态部分,故判断矩阵为:
根据前面的计算流程可以得到各个时间段的权重系数:
判断矩阵B的最大特征值
为4.0328,故判断矩阵B的一致性指标:
查表得到
,
。
判断矩阵符合一致性条件,再根据直流电压、电流的实测值与仿真值,可以计算出各个时间段曲线间的残差相似度与形状相似度,如表2所示。

Table 2. Similarity results of pole 1 DC voltage and DC current in Jiquan UHVDC
表2. 吉泉直流极1直流电压、直流电流相似度结果
从表2可以看出,吉泉直流的极1直流电压和直流电流在故障发生前的稳态、故障切除后的稳态以及故障过程中的暂态三个时间段的相似度指标均较高,尤其是两个稳态时间段时近似为1,故障发生后的暂态过程的相似度计算结果略低。根据式(5)及表1中的计算结果可以计算出此次实时仿真的仿真精度。如果
取值0.3,直流电压和直流电流的仿真精度分别为0.9392与0.9650;如果
取值0.7,直流电压和直流电流的仿真精度分别为0.9239与0.9599。从该精度评估结果可知,对于此次短路故障,直流电流的仿真精度要高于直流电压的仿真精度,选用不同的权值
,得到的仿真精度评估结果也会不同 [15] [16] 。
综合来看,仿真精度分析结果表明,仿真试验波形与现场实际波形吻合得比较好。定量分析与定性分析所得结论完全一致。通过仿真精度的综合评估,对试验结果的仿真精度做出了准确客观的评价。本文提出的仿真精度评估方法能综合考虑仿真测试结果与实际波形的残差相似度与形状相似度,对仿真精度的评估更加科学准确。
5. 结论
本文结合标准系数法提出了综合考虑仿真曲线与实测曲线的残差和形状两方面的电力系统全电磁暂态数字仿真模型精度评估方法,以2020年华东“9∙27”单相接地故障为实际算例,进行的仿真精度评估的结果表明:
1) 该方法相较前文介绍的其他精度评估方法,可以使系统分析人员更方便的了解仿真曲线各段与实测值的残差差异程度、变化趋势差异程度,尤其是可以从动态角度掌握曲线变化趋势相似度,为用户修正模型参数提供必要的参考信息。
2) 评估者对残差相似度与形状相似度的偏重不同,得出的仿真精度评估结果也将不同。通过合理设定曲线各段相似度的权重,可以得到更为合理的、符合评估要求的精度评估结果。
致谢
作者感谢陈绪江、彭丽、李壮和程昱在论文的撰写过程中提出的宝贵意见,以及彭红英、李小龙和刘子新等同事的帮助,尤其要感谢安宁、李亚楼以及田芳三位老师给予的悉心指导。
参考文献
NOTES
*通讯作者。