1. 偏转引力理论简述
1687年牛顿发现了万有引力 [1] ,1915年爱因斯坦在广义相对论 [2] [3] 中把引力等效成时空的弯曲,偏转引力理论 [4] [5] [6] 从微观作用机理上揭示了引力的作用过程。
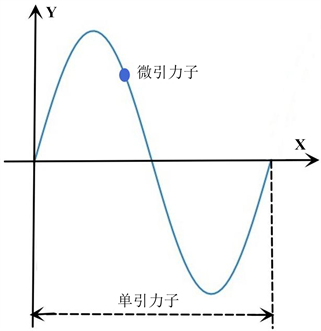
Figure 1. Microphotons and single photons
图1. 微引力子和单引力子
偏转引力理论认为:质量的最小单位为核子(质子和中子的统称),每个核子每秒可以发射大量引力子,每个核子同时每秒可以吸收大量个引力子,以保持核子质量的平衡。星球大量的核子发出巨量的引力子,其中大部分与星球内部的核子发生作用,形成星球内部的凝聚力,星球靠近外部的核子发出的引力子,部分发往星球外,以引力能量波的形式在空间传播形成引力线,星球周围四面八方的引力线形成星球的引力场,处在引力场中的物体,受到引力线上引力子的作用,会产生垂直于引力线的位移,这个位移平行于物体运动方向(切向)的分量,会影响物体的运行速度,这个位移垂直于物体运动方向(法向)的分量会影响物体的运行方向,处于两条引力线中间的物体,受到前后引力线的作用,会使物体运行方向会向星球方向发生偏转,形成星球与物质之间的引力。
这里的引力子为以波的形式传播的微引力子,也指引力能量波的单个波包,如图1所示。引力能量波的波长为:
(1)
引力能量波的频率为:
(2)
周期为:
(3)
通过对相邻核子之间的能量传递的计算 [7] ,可以得出穿过核子的引力子可以被核子吸收的比例:
(4)
由核子的结合能可以反推核子单位时间1 s内核子实际发出引力子的数量:
(5)
相应的单个核子1 s内吸收引力子的数量也为:
。
2. 星球发往球外引力子数量
图2为星球分层示意图,图中星球中心部分核子发出的引力子,会被星球内部其它核子吸收,形成星球内部的凝聚力,将大量物质聚到一起。星球靠近外层的核子发出的引力子,朝外的部分会有一部分发射到球外,以引力能量波的形式传播形成引力线,四面八方的引力线形成星球的引力场。一般的星球密度随着组成星球的物质不一样而变化,和物质与星球中心的距离也会发生变化,为了便于计算,我们把星球密度看成均匀的。
设星球的质量为ms,半径为rs,密度为ρs,它们之间的关系为:
(6)
(7)
(8)
设单个核子质量为m0,半径为r0,设星球中单个核子所占体积的等效半径为re,每个核子所占体积符合:
(9)
等效半径re为:
(10)
星球内核子总层数:
(11)
设kng为穿过核子的引力子能够被核子吸收的比例,
就是核子的有效面积,设ri层核子发出的引力子会被球内核子全部吸收,ri + 2re层所有核子的有效面积占当层总面积的比例:
(12)
ri + 4re层所有核子有效面积占当层总球面的比例为:
(13)
可见各层核子的有效面积占当层总球面的比例是一样的。
设球内核子可向球外发射引力子的总层数Nso为:
(14)
(15)
设球体可向球外发射引力子的外层厚度系数为ksρ,则这个厚度为:
(16)
对于每层核子,每个核子的一半多一点朝外,设这个比例为ko = 0.55,则星球发往球外的引力子总数为:
(17)
上面式(17)由Nso组的和组成,这里列出了前四组,第一组为ri + 2re核子层,也就是由内向外可以发射引力子到球外的第一层,第一项为当层的核子数,×单个核子发出的引力子数nng为当层发出总的引力子数,×向外的比例ko为当层向外的引力子总数,×核子能够穿过的锥角范围
范围,为当层核子可以发射到球外的引力子数,其余范围被核子有效面积全部覆盖,引力子无法穿透;公式中第二组为由内向外可以发射到球外引力子的第二层,以此类推。将式(17)公共项提出:
(18)
(19)
(20)
(21)
对上式中的数列分别求和:
(22)
一般的
所以:
(23)
(24)
将公式(10)、(14)、(16)代入:
(25)
化简:
(26)
(27)
(28)
(29)
代入常数并计算后:
(30)
设星球发往球外的引力子数和星球可以发出的引力子总数之比为k1:
(31)
3. 地球与太阳球外引力子数量
对于能够测定内部结构和密度的星球,可以更加精确的确定发射到星球外的引力子数量和球外引力子发射的核子层厚度。
3.1. 地球球外引力子数量
地球分地核,地幔和地壳三层,如图3。每层的密度不一样。地壳的厚度和密度为:
(32)
(33)
地球半径为:
(34)
壳层质量为:
(35)
地壳层核子等效半径为:
(36)
(37)
地壳层核子层数:
(38)
能够发射到球外引力子的层数:
(39)
,说明发射到球外引力子的核子全部由地壳层提供。引力子能够发射到球外的核子厚度为:
(40)
发射到球外的引力子数量:
(41)
可以看出发往球外引力子的核子层厚度随着地球壳层密度的减小而增加,发往球外的引力子数量没有变化。
3.2. 太阳球外引力子数量
太阳由日核区,辐射区,对流层,光球层组成,如图4。日核区半径为0.15~0.2个太阳半径,它的密度高达150,000 kg/m3,辐射层为0.15~0.86个太阳半径区域,对流层宽度为1.4 × 108 m,辐射对流层密度为800~18,000 kg/m3,光球层厚度5 × 105 m,密度各种资料不一致,比较合理的资料认为,光球的表面是气态的,其平均密度只有水的几亿分之一(水的密度是1 g/cm3),也有认为光球层密度约为地球表面空气密度的千分之一(空气密度约为1.29 kg/m³),还有资料显示光球层密度约为1023个原子/m³有些资料显示的光球层密度太大,这里取光球层密度为10 kg/m3,只是在现有资料基础上的估算,不能作为准确依据。
太阳光球层厚度和密度为:
(42)
(43)
太阳半径为:
(44)
光球层质量为:
(45)
光球层核子等效半径符合:
(46)
(47)
光球层核子层数:
(48)
能够发射到球外引力子的层数:
(49)
,说明发射到球外引力子的核子全部由光球层提供。引力子能够发射到球外的核子层厚度为:
(50)
引力子发射数量:
(51)
可以看出发往球外引力子的核子层厚度随着太阳光球层密度的减小而增加,发往球外的引力子数量没有变化。
3.3. 球外引力子数量公式30的简化
表1是太阳系各大星球可以向球外发射外引力子的核子壳层厚度,发往球外的引力子数量,和球外

Table 1. The number of gravitons emitted by the planets in the solar system to the outside world
表1. 太阳系星球发射到球外引力子数量
引力子数量和星球发射引力子总数的比例。
上表1中,E代表以10为低的幂,1.9891E+30表示1.9891 × 1030,其余类似。表中第二列ms为星球质量,第三列rs为星球半径,第四列ρs为星球密度或者星球最外层密度,第五列rso为可以发射到球外的核子层厚度,第六列nso为发射到球外的引力子数量,第七列nso(rs)为只有星球半径一项时,发射到球外的引力子数量,第八列k1为发射到球外引力子数量和星球发发射引力子总量的比值,最后一列为表格中用到的一些常数。r0为核子半径,m0为核子质量,nng为单个核子每秒发射引力子数量,ko为单个核子发往外部的核子比例,kng为穿过核子的引力子被核子吸收的比例。球外引力子数量与星球发射引力子总量的比例k1均值为:5.344 × 10−6,由表可以看出,星球可以向外发射引力子的只是星球靠外层薄薄的一个壳层,这层厚度平均不到星球半径的千分之一。星球发往球外的引力子数量随星球质量的增加而增加,但是并不成严格的线性关系,由表中第六列和第七列数值基本相等,可以看出,球外引力子数量公式30中主要有星球半径的一项形成,其它与星球密度有关的2项可以忽略。由此可以近似认为球外引力子数量与星球半径的平方成正比。球外引力子数量公式可以简化为:
(52)
4. 对万有引力的修正
牛顿在1687年提出了万有引力定律,公式如下:
(53)
牛顿万有定律反映了两个物体之间的作用力,但是并没有说明引力产生的微观机理。偏转引力理论认为:星球大量的核子发出巨量的引力子,其中大部分与星球内部的核子发生作用,形成星球内部的凝聚力,星球靠近外部的核子发出的引力子,部分发往星球外,以引力能量波的形式在空间传播形成引力线,星球周围四面八方的引力线形成星球的引力场,处在引力场中物体的每个核子单位时间都可以吸收大量的引力子,实现星球之间能量的转换,星球之间的引力,就是A星球发出的引力子与B星球核子发生能量转移的结果。
设星球A发射到球外的引力子比例为k1,B星球吸收球外引力子的比例为k2,万有引力公式可以理解两星球引力子的作用:
(54)
式中,m1/m0为星球A的核子数,m1/m0k1为星球A发射到球外的引力子数,m2/m0为星球B的核子数,m2/m0k2为星球B接受球外的引力子数,显然当k1与k2相等时,这与万有引力公式等价。上式直接用球外引力子数量表示:
(55)
代入52式:
(56)
简化后为:
(57)
公式中Gr为修正后的引力常数,上面修正后的引力公式与星球大小相关,与星球质量没有直接关系。星球的半径实际上代表了星球的表面积,对于非球形的星体,万有引力公式也可以表示为:
(58)
5. 结论
本文在偏转引力理论基础上,计算了星球发往球外引力子的核子层厚度rso = ksp/ρs,这个厚度与星球外层的物质密度成反比,一般不到星球半径的千分之一。计算了星球发往球外的引力子数量,这个数量随星球变大而增加,但是与星球质量并非严格的正比关系,对于大体积星球这个数量
,也就是说星球发往球外的引力子数量与星球半径的平方成正比,并由此修正了万有引力公式,说明引力与星球半径的平方成正比,也就是与星球的表面积成正比,与两星球距离的平方成反比。
常用符号和数据索引
核子(中子)质量m0 = 1.67 × 10−27 kg
核子(中子)直径r0 = 1.6 × 10−15 m
核子单位时间1秒内发射引力子数
nng = 6.318 × 1021
核子单位时间1秒内吸收引力子数量
nng = 6.318 × 1021
穿过核子的引力子吸收比例kng = 0.682
引力能量波的波长λ0 = 1.6 × 10−15 m
引力能量波的频率f0 = 1.875 × 1023 hz
引力能量波的周期T0 = 5.33 × 10−24 s
光速c = 3 × 108 m/s
普朗克常数h = 6.626 × 10−34J·s
万有引力常数G = 6.67 × 10−11 m3/(kg·s2)
偏转引力常数GD
的结合能为2.224 MeV
星球的质量ms
星球的半径rs
星球的密度ρs
星球中核子的等效半径re
球外引力子系数kgr = 2.54 × 1054
星球不能向外发射引力子的核子层半径rsi
星球向球外发射引力子的核子壳层厚度rso
发射到球外引力子的核子壳层厚度系数
ksρ = 22,956
星球中核子的分层层数Ns
星球不能向外发射引力子的核子层数Nsi
星球发往球外的引力子壳层核子层数Nso
星球所有核子发射引力子总数ng
星球发往球外的引力子总数ngo
星球发往球外的引力子比例k1
星球核子发往外部的引力子比例ko = 0.55
星球不能吸收球外引力子的核子层半径rsi
星球可以吸收球外引力子的核子壳层厚度rso
星球不能吸收球外引力子的核子层数Nsi
星球可以吸收球外引力子的壳层核子层数Nso
可以吸收球外引力子的核子壳层厚度系数
ksρ = 22,956
星球吸收引力子的总数ng
星球吸收球外引力子的总数ngo
星球吸收球外引力子的比例k2
星球核子吸收层外引力子比例ko
单个引力子被核子吸收的比例kR
太阳质量:1.9891 × 1030 kg
太阳半径:6.955 × 108 km
太阳密度:1.408 × 103 kg/m3.
地球质量:5.97237 × 1024 kg
地球半径:6371 × 106 m.
地球密度:5507.85 kg/m³
地球公转线速度:29,783 m/s
地球与太阳距离:1.496 × 1011 m