1. 引言
能源是经济社会的基石,化石能源的大规模开发和利用带来环境污染、气候变化等问题,以清洁能源为主导,以电为中心是能源的发展趋势和解决上述问题的关键 [1] 。然而,为改变纵向一体化的垄断局面,发挥电力市场作用,电力系统放松了管制,通过引入竞争机制,实现能源资源的有效配置。此外,电力市场还包括无功服务、削峰和调频等辅助服务 [2] ,其开放程度和范围较为深广。
程晓春等 [3] 认为应该妥善平衡市场监管与放松管制之间的关系,以实现市场改革目标。袁靖波等 [4] 建立了动态博弈论模型以研究放松市场管制对燃气发电的影响。Du [5] 重点研究了碳足迹和低碳偏好对市场供需的影响。
电力市场研究的关键问题是将经济学中的市场原理融入电力系统的实际运行中。其中,由于对现货电力市场竞价和辅助服务市场定价的同时适用,节点定价法极具代表性 [6] 。然而,节点定价法会造成分配不公的问题,因此,新的市场清算机制被提出以解决该问题。Baghayipour等通过修改系统节点价格,公平地清算市场并评估每个参与者的收入数额。然而,他们忽略了输电损耗的影响,故而进一步提出了一个新的节点定价机制,并建立一个公平和全面的定价框架以弥补上述不足 [7] [8] 。陈洋等 [9] 分析了网络损失和拥堵对电力现货市场的影响,并建立了一个考虑到网络损失和传输限制的全新平衡模型。
针对电力行业的特点,电力市场的实施难度很大,电力系统的安全运行也面临着很多隐患。因此,为了满足电力系统安全、可靠运行的要求,必须对电力市场进行严格监管。监管和放松监管是两个相反的概念。当监管的程度加强时,放松监管的程度就会降低,即市场竞争的程度也会降低。也就是说,电力市场不是充分竞争的,不是所有的资源在电力市场上都应该进行交易。
2. 有限竞争的电力市场清算模型构建
由于电网损耗和拥堵的存在,电力市场失灵出现,电力市场不完全竞争。为了量化交易比率,本文提出了一个有限竞争的电力市场清算模型。在所提模型中,只有部分电力参与市场竞争,这部分是绝对竞争的。不参与市场竞争的电力可以用于计划、调度等。而市场监管就在这个过程中进行,这与传统的运营模式类似。
假设每个节点的注入功率为
,且满足功率平衡方程
。设
,其中
表示参与电力市场竞争的电力;
表示不参与电力市场竞争的电力,在电力市场上受到管制。此外,
假设发电公司的产出为正,而用户的产出为负。有限竞争的电力市场可以描述如下 [10] :
(1)
其中,
和
分别是发电机有功功率的上限和下限;
是参与电力市场竞争的发电机k的有功功率;不等式约束
意味着发电机必须满足参与市场竞争的功率。如果是主动的,发电机将没有功
率来调整电力流,增加了网络拥堵的风险。
在有限竞争的电力市场中,自由电力交易(
)与电力网络的特性无关,不参与市场竞争的电力(
)被调整以满足网络损耗和拥堵。分解电力平衡方程,则上述数学模型变为:
(2)
进一步地,上述问题变成了如下的优化问题,它必须满足约束条件:
(3)
其优化问题为:
(4)
利用拉格朗日函数并对变量pk进行求导,可以得到:
(5)
其中
表示边际价格。进一步地,优化问题变为:
(6)
在满足约束条件(3)的前提下,电力市场可以达到均衡状态。在这个条件下,电力市场不受电力网络和交易模式特点的限制。
3. 自由交易率
如前文所述,只要满足约束条件(3),参与市场竞争的权力就会满足均衡原则。但是,如果市场交易是自由进行的,就不可能预测和控制交易量。因此,必须限制市场参与者的自由交易比率以满足约束条件(3)。
交易比率应该按照总供给或总需求的比率来确定。由于网络损失的存在,根据总供给或总需求定义的交易比率是不同的。假设
是根据总需求定义的交易比率,那么:
(7)
其中,
表示负荷功率;
为参与市场竞争的负荷的有功功率;
、
分别为未参与市场竞争的负荷和发电机的有功功率;
。
为了确定基于自由市场交易的最佳交易比率,根据约束条件(3),可以提出以下优化问题:
(8)
其中,
和
分别为负荷节点和发电机节点的数量。最小化的反函数是由发电机的投标价格得到的总发电成本。一般来说,它可以被描述为如下的二次函数:
(9)
其中,
表示二次成本系数;
是线性系数;
是发电机k的空载成本。参与市场竞争的电力越多,电力系统可能遭受的风险越大,导致不必要的电力网拥堵。因此,应仔细确定最佳交易比率,以满足约束条件(3)。
4. 案例研究
基于图1所示的IEEE-30节点测试系统,本章开展了三个案例研究,以分析不同自由交易比率对电力系统运行的影响,并确定最佳交易比率。所有情况都使用MATLAB中的MATPOWER工具箱进行模拟。测试系统由连接在节点1、2、5、8、11和13的六台发电机组成,发电机的运行特性见表1。假设参与自由市场竞争的发电机的初始功率为
MW,负荷的总需求为283.4 MW。

Table 1. Generator operating parameters
表1. 发电机运行参数

Figure 1. IEEE-30 node test system
图1. IEEE-30节点测试系统
案例1:参与自由市场竞争的发电机的初始总功率为250 MW。由于参与自由市场竞争的发电机的功
率被用来供应参与自由市场竞争的负荷,自由交易率为
。发电机节点的市场交易情况
如表2所示。为了明确说明负荷节点的市场交易情况,参与自由市场竞争的负荷的结果如图2所示。

Table 2. Case 1: generator node market transactions
表2. 案例1:发电机节点市场交易
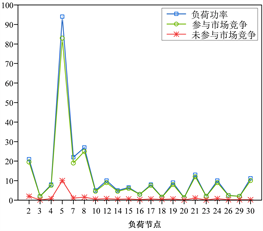
Figure 2. Case 1: load node market trading
图2. 案例1:负荷节点市场交易
根据结果,网络损失为295.15 − 283.4 = 11.75 MW。没有输电线路超出功率流限制,所以不存在输电拥堵。参与自由市场竞争的发电机的总功率与参与自由市场竞争的负荷的总功率相等。发电机和负荷的剩余功率用于平衡网络损失,它们的差值为11.75 MW。
案例2:以相同的比率增加负荷节点参与自由市场竞争的数量,直到有一些发电机处于其市场交易极限。此时,自由交易比率为
。表3显示了这种情况下发电机节点的市场交易情况,图3说明了负荷节点的市场交易情况。

Table 3. Case 2: generator node market transactions
表3. 案例2:发电机节点市场交易
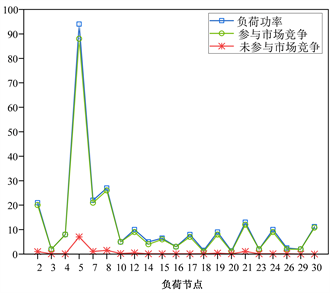
Figure 3. Case 2: load node market trading
图3. 案例2:负荷节点市场交易
在这种情况下,网络损失为11.76 MW,没有输电线路拥堵。1号发电机的有功功率达到了市场交易限额。事实上,当
时,随着自由市场交易的增加,将不存在有功发电和输电拥挤的限制。将表3中的数据与表2中的数据进行比较,可以看出,最佳调度并没有受到参与自由市场竞争的电量增量的影响。发电机的产出和发电成本几乎保持不变。
案例3:交易比率为
。这是一个极端情况,所有的负荷节点都参与了自由市场交易。发电机和负荷节点的市场交易情况分别如表4和图4所示。网络损失为13.21 MW,输电线路1-2拥堵(
)。1号和8号发电机在其下限运行。没有参与自由市场竞争的发电机的功率被用来平衡网络损耗。可以看出,网络损失和发电成本都在增加。

Table 4. Case 3: generator node market transactions
表4. 案例3:发电机节点市场交易
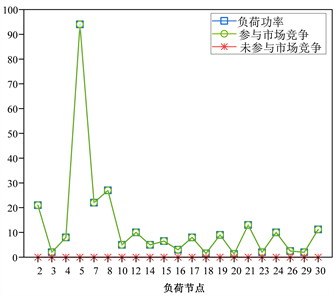
Figure 4. Case 3: load node market trading
图4. 案例3:负荷节点市场交易
三个案例研究的模拟结果总结于表5。其中,案例1为参考案例;案例2为关键案例,案例3为极端案例。所有案例都说明,参与自由市场竞争的电力与电网的特性无关,其余电力负责调整电力流和分配电网损失。由于案例2是1号发电机只是在其下限运行的临界情况,对于0到0.936之间的任何水平的交易比率,最佳调度都不受影响,所以
可以被视为最佳交易比率。在这个交易比率下,可以实现电力市场参与者的利润和效用的最大化。

Table 5. Final results of three cases
表5. 三个案例最终结果
自由交易比率的引入使得将电力分为两部分成为可能:参与自由市场竞争的电力和不参与自由市场竞争的电力。前者是完全竞争性的,后者是受管制的,只用于调整电力流和分配网络损失。自由交易比率可以被视为衡量电力市场放松管制的程度。参与自由市场竞争的电力越多,电力系统可能遭受的风险越大,导致不必要的电力网络拥堵。因此,有必要确定最佳交易比率。
注意,具有有限竞争的市场清算模型是在生产者和消费者充分了解电力网络损失和拥堵状况的基础上开发的。换句话说,市场参与者之间不存在信息不对称。只有这样,电力市场参与者的竞价价格才能反映电力网络的拥堵和损失。此外,才能实现最优的自由交易比例,达到电力市场均衡。
为解决信息不对称问题,生产者和消费者都需要了解实时市场数据。这些市场数据包括电力价格、电力网络损失和拥堵状况等。由于这些市场数据量大、流动快、多样性高,需要运用大数据理论来处理这些数据。通过大数据的应用,市场参与者可以全面了解电力网络状况,从而做出最优的生产或消费决策。
5. 结论
由于电力行业和电力市场的特殊性,一般均衡很难在电力市场得到满足。因此,必须对电力市场进行严格监管。本文分析了电力市场的失灵,提出了有限竞争的电力市场清算模式,以自动实现电力市场的均衡。可以得出以下一些结论。
(1) 电力市场并非完全竞争的市场,而是有限竞争的市场。电力市场由于其特殊性,如高度资本密集、技术壁垒、政策监管等,使得市场竞争程度受到一定限制。
(2) 电力市场的调节可以通过限制参与自由市场竞争的电力的交易比率来进行。电力市场交易比率受网络拥堵程度和损失情况影响。在电力市场中,交易比率限制是一种有效的调节手段。通过调整交易比率,可以引导电力公司合理安排发电和用电计划,降低网络拥堵和电力损失。
(3) 完全竞争市场的一个核心特征是市场参与者可以自由进入和退出市场,没有任何障碍。在这样一个市场中,交易模式不会对市场竞争产生限制。然而,在现实生活中,交易模式可能会对市场竞争产生影响,但这并不意味着完全竞争市场不能被交易模式所限制。在一定条件下,通过优化交易模式,有助于提高市场竞争力,促进市场参与者之间的公平竞争。
尽管受到诸如电力网络安全、交易模式、交易过程透明度和市场利益分配公平性等诸多限制,电力市场仍在许多国家得到实施。具有有限竞争的电力市场仅是一种学术观点,现货电力市场的自由交易比例也是一种调控方法。从微观经济角度来看,通过电力市场的调控,可以实现电力资源的有效分配。如参考文献 [11] 所述,采用平均成本定价可以在电力池模型中实现人工市场均衡。换句话说,电力池模型可以视为市场调控的方法之一。
参考文献