1. 研究背景
近年来,如何应对气候变暖问题已成为全球热点。习近平总书记于2020年9月22日在第七十五届联合国大会上向世界郑重宣布中国“双碳”目标,即二氧化碳排放力争于2023年前达到峰值,努力争取2060年前实现碳中和。在中国经济迅速发展的同时面临着越来越大的二氧化碳减排压力。基于大气二氧化碳浓度长期连续的观测,可实时反映二氧化碳的动态变化情况,还可反映二氧化碳年际变化趋势,这对全面理解与预测未来全球变化、温室效应尺度及其对社会经济的影响意义重大。为此,本文拟从省级尺度研究中国31省市二氧化碳排放量情况,分析2020年二氧化碳排放量季节变化趋势以此研究中国31省市二氧化碳排放量空间分布,对2011年~2020年10年来的二氧化碳排放情况进行分析以此对2021~2025年碳排放量进行预测。
2. 研究现状
近年来,国内外学者针对碳排放的时空变化格局和影响因子做了大量研究。研究范围主要集中在全国、省域和市域,研究内容主要包括碳排放量的核算、区域差异和格局演变以及影响因素等。如王兴民等从城市尺度来研究中国CO2排放的空间分异特征和驱动因子的影响 [1] 。邓吉祥等分析了中国八大区域碳排放的区域格局变化特征及探讨了影响区域碳排放变化的原因 [2] 。祁强强等人认为从时空尺度把握碳排放分布规律,量化区域碳排放的主导因素,对于确定减排的重点区域和调控要素具有重要的指导意义,并指出了经济发展和产业结构仍是碳排放量增长的主要原因 [3] 。田娟娟,张金锁两人通过研究发现碳排放量空间格局发生了显著的变化,2000年及2005年碳排放呈现“西低东高”“北高南低”的空间分异特征,而2010年及2017年碳排放逐渐呈现不平衡的空间分异特征,高碳排放区向东南及西北移动趋势日趋明显 [4] 。一些研究者从城市尺度研究了中国CO2排放的空间分异特征和驱动因子的影响,分析了中国八大区域碳排放的区域格局变化特征及变化原因。综上,大多数学者都强调了从时空尺度把握碳排放分布规律的重要性。因此,我们将在学者研究的基础上,将其研究成果与所查找的数据资料结合在一起,做出更深入的分析。
3. 研究对象与方法
3.1. 研究对象
本文以中国除港澳台地区外的31个省市从2011年到2020年二氧化碳的排放量为研究对象,主要对二氧化碳排放量的时空分布及2021~2025年碳排放量预测做出研究。
3.2. 数据来源
本文在综合现有研究现状的基础上,根据31个省市从2011年到2020年二氧化碳的排放量数据进行预测。二氧化碳排放量的数据由中国能源数据库(http://www.stats.gov.cn/sj/ndsj)、中国核算数据库(https://www.ceads.net.cn/)提供。
3.3. 研究方法
3.3.1. 文献资料法
通过查阅与本次研究有关的图书资料及论文文献,深度分析国内外相关领域的研究现状,为该研究提供理论依据;检索大量的能源数据库,对本文章的撰写提供数据支持与预测基础。
3.3.2. 数理统计法
运用SPSSPRO对31个省市从2011年到2020年二氧化碳的排放量的数据结果进行统计学处理与分析。通过其对原始数据的整理分析,可以获得十年来二氧化碳排放量的时间分布及其变化趋势,其得到的统计值可作为其它评价方法的基础资料。
3.3.3. 空间插值法
空间插值是通过已知点或分区的数据,推求任意点或分区数据的方法,常用于根据离散的采样点来获取连续的表面,包括空间内插和外推两种方法。空间内插提供一种从有限的已知样本点中估计同一区域中其他任意位置的值的方法,外推则是通过已知区域的数据来推求其他区域数据的方法。插值分析可以由有限的采样点数据,估计周围的数值情况,从而掌握研究区域内数据的总体分布状况,使得离散的采样点不仅仅反映其所在位置的数值情况,而且可以反映区域的数值分布 [5] 。
目前SuperMap中提供三种插值方法,用于模拟或者创建一个表面,分别是:距离反比权重法(IDW)、克吕金插值方法(Krging)、径向基函数插值法(RBF)。选用何种方法进行内插,通常取决于样点数据的分布和要创建的表面类型。无论选择哪种插值方法,已知点的数据越多,分布越广,插值结果将越接近实际情况 [6] 。
3.3.4. 数据标准化
数据标准化主要是消除变量间的量纲关系,使各指标值处于同一数量级别,从而可以确保数据的一致性、可靠性和可比性。标准化处理公式如下所示:
其中
和
分别表示
和
的均值 [7] 。
3.3.5. 预测
(1) 灰色预测模型GM(1,1)
灰色系统理论的特点是能够在有限的数据样本中充分挖掘利用其中的信息,为解决少量数据难以预测的问题提供了解决方案。灰色模型与其他模型的最大区别在于该模型具有灰色累加算子,这是其他模型所不具备的 [8] 。
本文在SPSSPRO中用时间序列对中国31省市2011~2020年的碳排放量数据进行级比检验建立灰色GM(1,1)时间序列为等间距模型进行预测。
设
,若间距Δ𝑡_𝑘 = 𝑡_𝑘 − 𝑡_(𝑘 − 1) ≠ c,k = 2,3, …, n,则称该序列为非等间距序列。
为
的r阶累加序列,其中
r的取值范围为0 < r ≤ 1 [8] 。
本文使用MAPE作为衡量模型有效性的标准,如公式所示。
表1为预测模型评价标准,用以说明MAPE的取值范围。一般情况下认为当MAPE在10%以下时该模型有较高的预测能力 [9] 。

Table 1. Prediction model evaluation criteria
表1. 预测模型评价标准
(2) 线性回归预测模型
本文对各省市2011~2020年的碳排放量数据的采用线性回归(一般二乘法)的方法,得出y = bx + a的回归方程,从而利用方程对2020年之后的五年二氧化碳排放量进行预测。一般地,影响y的因素有多个,假设有x1,x2,...,xk,k个因素,通常可考虑如下的线性关系式:
对y与x1,x2,…,xk同时作n次独立观察得n组观测值(xt1, xt2, ..., xtk),t = 1, 2,…, n (n > k + 1),它们满足关系式:
其中,ε1,εn互不相关均是与ε同分布的随机变量。于是有Y = Xβ + ε,使用最小二乘法得到β的解
,其中,
称为X的伪逆 [10] 。
4. 中国31省市碳排放结果与分析
4.1. 中国31省市碳排放时间分布
通过分析2011年到2020年二氧化碳的排放量数据,研究中国除港澳台地区外的31个省市二氧化碳排放量的时间变化,结果如图1所示。
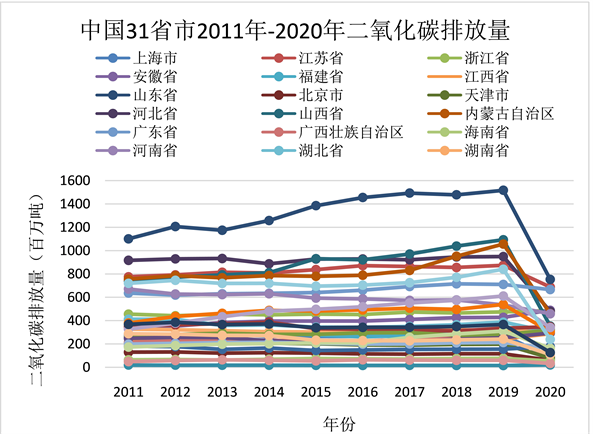
Figure 1. Carbon dioxide emissions from 31 provinces and cities
图1. 31省市二氧化碳排放量
从(图1) 31省市二氧化碳排放量曲线图可以看出:各省市在2011~2020年二氧化碳排放量整体变化趋势一致。大体的趋势是在2011~2019年逐渐增加,大多数省市在2019~2020年中二氧化碳的排放量又大幅减少。
在2011~2019年期间,二氧化碳逐渐增加的原因主要有三方面:一是随着经济迅速增长,我国现阶段产业结构不断调整,高耗能产业占有相当大比重,因此带来大量的碳排放;二是我国的能源消费结构以煤炭为主,导致了碳排量的增加;三是随着人口的剧增和工业化的发展,人类社会对化石燃料的需求急剧增加,从而导致二氧化碳排放量的快速增长。
在2019~2020年期间,大多数省市二氧化碳排放量减少的原因是:中国政府采取了一系列措施,如推广清洁能源、加强工业和交通领域的节能减排、加强碳交易等,来减少碳排放。2019年到2020年,疫情期间全国大部分地区碳排放量创新低,但仍然有省份不减反增加,浙江省、安徽省、福建省、江西省等部分华东及沿海省份疫情期间由于油轮活动限制,导致主要海港污染物排放量激增,另外由于2020年的下半年疫情回缓后,作为国内最大的碳排放区域的华东省份复工复产后产业能源消耗,因此二氧化碳排放量就上升得很快,总量变化仍为上升趋势。而重庆市、四川省、贵州省、云南省、西藏自治区、广西壮族自治区等部分西南与南部省份相较于全国其它地区,受疫情的影响较小,各领域复苏较快,维持经济发展仍需要大量的煤炭能源消耗,所以碳排放量仍在增长。
4.2. 中国31省市碳排放空间分布
为分析二氧化碳排放量空间分布特点,根据气候统计法,本文采用四季分类的方法。气候统计上,3、4、5月为春季,6、7、8月为夏季,9、10、11月为秋季,12、1、2月为冬季。
通过SuperMap iDesktop软件,运用空间插值法,本文得到中国除港澳台地区外的31个省市春、夏、秋、冬四季二氧化碳排放量的空间分布,如图2所示。

Figure 2. Spatial distribution of carbon dioxide emissions in 31 provinces and cities
图2. 31省市二氧化碳排放量空间分布图
在2020年中,各省市在夏季的二氧化碳排放量最多,总排放量为2590.18百万吨;在秋季二氧化碳排放量最少,总排放量为2172.61百万吨。
华东地区在一年四季中二氧化碳排放量都位居前列,其碳排放量主要来自山东和江苏两省,二省合计占华东地区总排放量的50%以上,山东和江苏都是中国东部沿海的主要制造业中心,山东的能源、工业和农业部门也很强大,所以二氧化碳排放量较多;而东北地区二氧化碳排放量相对较少,原因是该地区的能源利用效率偏低,这意味着在能源消耗过程中,碳排放量可能相对较低。碳排放量的影响因素可能基于低碳经济视角,这意味着在经济发展过程中,可能更注重减少碳排放,从而降低了碳排放强度。
4.3. 中国31省市碳排放预测
根据上述设定数据构建的基准情况,以年份为自变量X (2011年为自变量1),对2011年~2020年中国31省市二氧化碳的排放量进行线性回归预测模型建立,见表2,据此对2021~2025年中国31省市总二氧化碳排放量进行预测。

Table 2. Prediction model for carbon dioxide emissions in 31 provinces and cities in China from 2011 to 2020
表2. 2011年~2020年中国31省市二氧化碳排放量预测模型
由于2019年~2020年受疫情的影响,用线性回归模型研究中国31省市二氧化碳排放量年份与年二氧化碳排放量之间线性回归关系,得出结果:F检验的显著性P值为0.812,水平上不呈现显著性,不能拒绝回归系数为0的原假设,模型无效。所以直接用线性回归模型预测中国31省市总二氧化碳排放量预测是无效的。

Table 3. Grade comparison inspection result table
表3. 级比检验结果表
在SPSSPRO中用时间序列进行级比检验,通过级比检验,见表3级比检验结果表,从表中分析可以得到,平移转换后序列的所有级比值都位于区间(0.834, 1.199)内,说明平移转换后序列适合构建灰色预测模型 [11] 。

Table 4. Model Fitting Results Table
表4. 模型拟合结果表
从表4得出结果:模型平均相对误差为6.821%,意味着模型拟合效果良好,因此采用灰色预测模型GM(1,1)进行预测。预测结果如表5所示。

Table 5. Predicted total carbon dioxide emissions from 31 provinces and cities in China from 2021 to 2025
表5. 中国31省市2021~2025年总二氧化碳排放量预测值
5. 结论与讨论
根据已有的数据和趋势分析,未来中国各省市的二氧化碳排放预测如下。
5.1. 总体趋势
在当前政策和经济发展情况下,中国的二氧化碳排放量总体下降,但稍高于2020年,预计到2025年,中国的温室气体排放将达到11793.108百万吨。
5.2. 区域差异
中国各省市在二氧化碳排放上存在明显的区域差异。
5.2.1. 空间分布方面
东部沿海地区,经济发达、人口密集一年四季中二氧化碳排放量都位居前列;而在西部地区,经济相对落后、人口较少,二氧化碳排放量最少;各省市在夏季的二氧化碳排放量最多,在秋季二氧化碳排放量最少。
5.2.2. 时间分布方面
各省市在2011~2020年二氧化碳排放量整体变化趋势一致。大体的趋势是在2011~2019年逐渐增加,大多数省市在2019~2020年中二氧化碳的排放量又大幅减少。预计未来这种区域差异将继续存在。
5.3. 产业结构调整
随着国家产业结构的优化调整,高能耗、高排放的产业将逐渐向低能耗、低排放的产业转型。这将导致部分省市的二氧化碳排放量下降,但在一些重工业基地和能源产区,排放量仍将保持较高水平。
5.4. 节能减排政策
随着国家对节能减排的重视程度加大,未来政府将采取更加严格的政策措施,推动各省市实施节能减排。这将有助于降低各省市的二氧化碳排放。
综合考虑以上因素,未来中国各省市在二氧化碳排放上的预测呈现出以下特点:总体上,二氧化碳排放将慢慢减少;区域差异明显,东部地区排放量较高,西部地区排放量较低。
基金项目
本项目为楚雄师范学院地理科学云南省一流专业建设点项目成果。
NOTES
*通讯作者。