基于CF-PSPnet的主波束效应的校正研究

Correction Study for Primary Beam Effect Based on CF-PSPnet

摘要: 射电天文成像过程中，需要对观测得到的脏图进行反卷积操作得到“干净”的图像，而这图像中包含着主波束效应，未得到主波束效应校正的图像在偏离中心区域的地方会出现强度衰减的现象，而且距离中心越远，衰减现象越明显。传统的主波束校正方法虽然能够完成校正，但对于图像边缘区域尤其是微弱结构的细节恢复的不是很理想。因此，本文提出了CF-PSPnet的深度学习的模型，引入了注意力机制，多特征融合等操作，实现了对观测图像中不同级别特征的融合与提取，从而达到对主波束校正的需求。经本文实验后得出，CF-PSPnet解决了传统图像域校正方法中存在的缺点，有着不错的校正效果。下一代的射电天文望远镜有着更高灵敏度，动态范围与空间角分辨率，本文方法为其主波束效应校正提供了一种更具潜力的解决方案。

Abstract: In the process of radio astronomy imaging, it is necessary to deconvolve the dirty image obtained from observation to obtain a “clean” image, which contains the primary beam effect, and the image not corrected for the primary beam effect will have intensity attenuation in the off-centre area, and the further away from the centre, the more obvious the attenuation phenomenon. Although the traditional primary beam correction method can complete the correction, it is not ideal for the image edge region, especially for the recovery of the details of the weak structure. Therefore, this paper proposes a deep learning model of CF-PSPnet, which introduces the attention mechanism, multi-feature fusion and other operations to achieve the fusion and extraction of different levels of features in the observed image, so as to achieve the demand for the primary beam correction. After the experiments in this paper, it is concluded that CF-PSPnet solves the shortcomings of the traditional image domain correction method and has good correction effect. The next generation of radio astronomy telescopes has higher sensitivity, dynamic range and spatial angular resolution, and the method in this paper provides a more promising solution for its main beam effect correction.

1. 引言

在射电干涉成像中，来自宇宙的电磁信号被天线接收，然后经过相关器，最终得到可见度信号。然而，天线所接收的信号与天线孔径的孔径照明函数有关，主波束就是孔径照明函数的傅里叶变换形式。在射电天文学中用干涉射电望远镜进行的天文观测中存在各种可变的增益，其可分为方向相关与方向无关两种 [1] 。而方向相关效应的其中之一便是主波束效应。而对于大部分El-Az天线，随着时间的变化也就是地球的转动，天线指向也会随着观测目标进行变化，这会导致时变效应 [2] 的出现，综合看来，方向相关的主波束效应变得十分复杂 [3] 。作为深度学习在主波束效应方面的初步应用，本文初步只对主波束方向相关效应校正进行了研究，主要表现在源的方向相关效应一致，即1) 方向相关效应相同(与频率，天线无关)；2) 效应与时间无关。本文所讨来的主波束效应主要表现为射电望远镜天线的主要辐射方向或响应方向上，望远镜的天线会将能量集中在主波束的方向，以最大化特定射电源信号的接收。这虽然能够在波束中心部分范围内实现良好的观测，但是在远离相位中心的位置，所观测信号强度会出现不同程度的衰减。这严重影响延展源与大尺度结构的观测，针对射电天文中主波束的这一衰减效应，传统的方法是图像域校正方法。在此方法中首先估计主波束的波束模型，然后直接用最终得到的观测图像除以波束模型，这种简单直接的方法虽能校正主波束的衰减效应，但是缺点却是相当明显，这种方法会增加图像边缘区域的噪声 [4] 。

目前已知深度学习在射电天文方面应用的案例，比如，Tanoglidis等人 [5] 提出使用深度CNN (Convolutional Neural Network)来完成将LSBG (Low-Surface-Brightness Galaxies)与调查图像中的伪影分离的任务。Czech等人 [6] 提出了一种基于CNN和LSTM (Long Short-Term Memory)的瞬态射频干扰分类方法。Cabrera-Vives等人在 [7] 提出了一种旋转不变的CNN模型，用于将瞬态候选图像分类为伪影或高节奏瞬态调查的真实来源，此外还有众多天文图像去噪，去模糊，超分辨率图像重建，脉冲星搜寻 [8] 等一系列应用。这些都是深度学习在射电天文方面的一些应用，受到这些应用的启发，本文决定将深度学习技术应用于主波束校正方面。

本文提出了一种基于深度卷积神经网络的深度学习模型用于实现主波束效应校正。本文提出的深度学习模型在主波束效应校正方面有以下特点：

1) 可以快速的分析提取主波束效应天文图的特征。

2) 效应校正更加高效且精准。

3) 模块化网络，方便后续迁移与拓展。

本文深度学习的探索包括从输入图像分析，网络模型构思，模型搭建，数据集构建，模型训练与验证等一系列操作，并引入了多个评价指标对深度学习的校正效果进行了客观评价。

2. 天线主波束及传统图像域校正方法

Hamaker等人提出射电干涉仪测量方程 [9] ，如式(2.1)所示，其中 $G_p$ 表示方向无关的效应， $B_{pq}$ 表示方向相关的效应，如式(2.2)所示。为新的校准方法和技术的发展提供了严格的数学基础，包括解决方向相关效应(DDEs)问题的各种方法。

$V_{pq}=G_p\left({\displaystyle \iint B_{pq}{\text{e}}^{-2\pi i\left(u_{pq}l+v_{pq}m\right)}\text{d}l\text{d}m}\right)G_q^H$ (2.1)

$B_{pq}=E_{p}B{E}_q$ (2.2)

对于辐射到天线孔径的电磁辐射，通常用孔径照明函来描述其空间分布，从数学角度方面来看，孔径照明函数又可以表示为孔径内空间坐标的函数(空间坐标通常由方位角和仰角来表示)，以用来描述各个方向辐射的响应或灵敏度。图1清楚的描述了孔径照明函数与天线各个参数之间的关系 [10] 。

Figure 1. Parametric relationships for interference domain antennas

图1. 干涉域天线的参数关系

在射电天文中，对于一对天线(孔径有限)，其连线被称为基线。干涉仪的每个基线对都对应着一组空间频率。因此将被观测源的可见度函数与基线所对应的空间频率的孔径函数进行卷积，结果就是基线对所测量到的可见度数据。其中，基线孔径函数为天线对的两个天线的光圈孔径函数的卷积，其傅里叶变换便为主波束。在可见度域中，可见度函数卷积光圈函数与天空亮度分布乘以主波束之间存在傅里叶对应关系 [11] 。

对主波束 $\left[P_b\right]$ 乘以实际亮度 ${\stackrel{\to }{I}}^{sky}$ 的结果进行傅里叶变换，然后干涉仪对其进行采样，采用反卷积对其进行处理，得到实际可见度 ${\stackrel{\to }{V}}^{corr}$ 。如式(2.3)所示，其中[F]为傅里叶变换操作符，[S]为采样矩阵。

$\left[S\right]\left[F\right]\left\{\left[P_b\right]{\stackrel{\to }{I}}^{sky}\right\}={\stackrel{\to }{V}}^{corr}$ (2.3)

用反傅里叶变换对 ${\stackrel{\to }{V}}^{corr}$ 进行操作，得到脏图 $I^D$ ，如式(2.4)所示。对脏图进行反卷积操作 [12] 处理得到 ${\stackrel{\to }{I}}^{decov}$ ，即主波束 $\left[P_b\right]$ 和真实天空亮度 ${\stackrel{\to }{I}}^{sky}$ 的乘积 ${\stackrel{\to }{I}}^{model}$ ，如式(2.5)所示，其中D为反卷积操作。如式(2.6)所示，用 ${\stackrel{\to }{I}}^{model}$ 除以主波束，可以得到天空亮度分布 ${\stackrel{\to }{I}}^{model,corr}$ 。

$I^D=F^{-1}\left[S\right]*\left\{\left[P_b\right]{\stackrel{\to }{I}}^{sky}\right\}$ (2.4)

${\stackrel{\to }{I}}^{model}={\stackrel{\to }{I}}^{decov}=D\left\{I^D\right\}$ (2.5)

${\stackrel{\to }{I}}^{model,corr}={\stackrel{\to }{I}}^{model}/P_b$ (2.6)

但是这种主波束校正方法也存在的明显的缺点，那就是校正会带来图像噪声的增加，而且越远离相位中心，噪声增加就会越明显。因此本文提出用深度学习的方法来对主波束效应进行校正。

3. 方法

为了实现对主波束效应的校正，本文提出了CF-PSPnet模型，该模型在PSPnet模型 [13] 基础上进行了的改进(如图2所示)，本文加入了混合注意力模块，空间残差连接，以及不同级别的特征融合，实现了将语义分割模型 [14] 向图像恢复模型的转变，在主波束效应校正方面表现出色。

Figure 2. PPSPnet model architecture diagram

图2. PSPnet模型架构图

3.1. CF-PSPnet网络模型

如图3所示，本文模型CF-PSPnet的输入图片是带有主波束效应的图片，该模型在PSPnet模型的基础上增加了CBAM (Convolutinal Block Attention Module)混合注意力模块，并且融合了不同尺寸的特征，加入了残差连接，最终形成本文的CF-PSPnet模型。

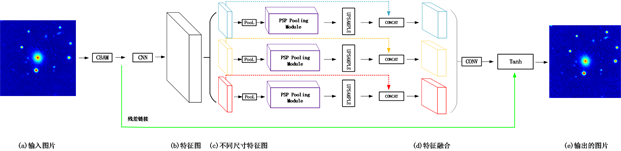
Figure 3. CF-SPnet model architecture diagram

图3. CF-SPnet模型架构图

CF-PSPnet模型的生成特征图部分的主体网络为Resnet，由三层CNN组成，如图4所示。本部分一共由101层CNN组成，其中包含3次下采样操作，共得到184 × 184，92 × 92，46 × 46三种尺寸的特征图。

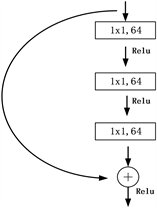
Figure 4. Resnet model architecture diagram

图4. Resnet模型架构图

混合注意力机制是深度学习方面常常用到的一种注意力模块，如图5所示，它结合了通道和空间的注意力机制模块，分别进行通道和空间上的Attention操作。

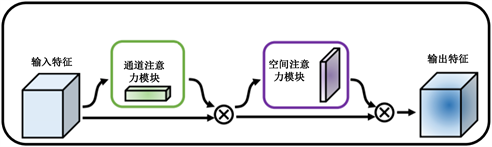
Figure 5. CBAM model architecture diagram

图5. CBAM模型架构图

最后，本文加入了从输入端到输出端的残差连接，实现了将语义分割到图像恢复的转变。残差连接，能够保证原输入图中的细节的保存，在模型训练中能够起到细节约束与补充信息的效果，最终达到更好的图像校正作用。

3.2. 损失函数

损失函数是深度学习模型训练的必备要素，通常用来表示模型训练真实值与输出值之间的差异。反向传播时，以损失值最小为目标，模型中的参数不断被更新，给模型的优化指明方向，因此损失函数是否合理是就显得非常重要。

常见的损失函数按使用用途可以分为回归类损失函数与分类损失函数。本文的损失函数属于回归方面的种类。常见的回归类损失函数有L1 Loss，L2 Loss函数。

L1 Loss指的是模型真实值与输出值之间实际距离的平均值，被称为平均绝对误差(MAE, Mean Absolute Error)，如式(3.1)所示。其中 $y_i$ 为模型的真实值， $f\left(x_i\right)$ 为模型的输出值。

$L=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}\left|y_i-f\left(x_i\right)\right|}$ (3.1)

由式(3.1)可以看出，L1损失函数对输入值有着广泛的普适性，梯度稳定。但不足之处是在中心折线处不能求导。

L2 Loss模型真实值与输出值之间实际距离平方的平均值，也被称为均方误差(MSE, Mean Square Error)，如式(3.2)所示。其中 $y_i$ 为模型的真实值， $f\left(x_i\right)$ 为模型的输出值。

$L=\frac{1}{n}{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left(y_i-f\left(x_i\right)\right)}^2}$ (3.2)

由式(3.2)可以看出，由于L2损失与二次方有关，所以不存在L1 Loss那种折线处不能求导的情况。同时，由于二次方的关系，当模型真实值与预测值之间的距离变大时，使用梯度下降法容易产生梯度爆炸的情况。本文中，如式(3.3)所示，采用的损失函数为Huber Loss，y为实际值， $f\left(x\right)$ 为输出值， $\delta$ 为Huber Loss的参数。

$\{\begin{array}{l}\left|y-f\left(x_i\right)\right|\le \delta 保证梯度得到更精确的收敛值\\ \left|y-f\left(x_i\right)\right|>\delta 保证模型能更快的参数更新\end{array}$ (3.3)

由式(3.3)可以看出，Huber Loss有效的解决了L1 Loss与L2 Loss的折线处不能求导与梯度爆炸的问题。

4. 实验

4.1. 数据集

Figure 6. (Left) Observation model; (Right) Observations data (with primary beam effects)

图6. (左)观测模型；(右)观测数据(含主波束效应)

模拟本文模拟观测采用CASA (the Common Astronomy Software Applications)天文模拟软件 [15] 进行了模拟观测，其中使用了VLA_C配置，支持观测频率范围为4 GHz~8 GHz，以2 GHz为步频，得到4 GHz，6 GHz，8 GHz 3个观测频段。使用galaxy zoo中下载的星系图像为观测模型，观测时间6小时，其中观测中含有主波束效应。

观测模型与含有主波束效应的观测图像的伪彩图如图6所示，其可以作为一组训练对。400个数据对用于训练集用与训练阶段，150个数据对在验证与测试中使用。

4.2. 评价指标

为了评价矫正模型的实际效果，本文使用峰值信噪比(PSNR, Peak Signal-to-Noise Rati) [16] 、结构相似性(SSIM, structural similarity) [17] ，作为本文图像质量的评价指标。

PSNR常用于图像处理领域，是一种评估图像质量的指标，通过比较原始图像和重建图像之间的均方误差(MSE)来计算。PSNR值越高，表示图像的质量越好。式(4.1)定义了两幅图像I，K之间的均方差，图像尺寸为(m, n)。

$\text{MSE}=\frac{1}{mn}{\displaystyle \underset{i=0}{\overset{m-1}{\sum }}{\displaystyle \underset{j=0}{\overset{n-1}{\sum }}{\Vert I\left(i,j\right)-K\left(i,j\right)\Vert }^2}}$ (4.1)

$\text{PSNR}=10{\log }_{10}\left(\frac{{\text{MAX}}_{\text{I}}^{\text{2}}}{\text{MSE}}\right)=20{\log }_{10}\left(\frac{{\text{MAX}}_{\text{I}}}{\text{MSE}}\right)$ (4.2)

式(4.2)即为峰值信噪比定义。其中，MSE为两图像I，K的均方误差，MAX_I表示图像点像素的最大值。结构相似性，是一种衡量两幅图像相似度的指标。它从图像组成的角度将结构信息定义为独立于亮度、对比度的，反映场景中物体结构的属性。结构相似性的范围为−1到1，当两张图像一模一样时，SSIM的值等于1。

$\text{SSIM}={\left[l\left(x,y\right)\right]}^{\alpha }{\left[c\left(x,y\right)\right]}^{\beta }{\left[s\left(x,y\right)\right]}^{\gamma }$ (4.3)

$I\left(x,y\right)=\frac{2{\mu }_x{\mu }_y+C_1}{{\mu }_x^2{\mu }_y^2+C_1}$ (4.4)

$c\left(x,y\right)=\frac{2{\sigma }_x{\sigma }_y+C_2}{{\sigma }_x^2{\sigma }_y^2+C^2}$ (4.5)

$l\left(x,y\right)=\frac{2{\sigma }_{xy}+C_3}{{\sigma }_x{\sigma }_y+C_3}$ (4.6)

式(4.3)定义了信号x，y之间的结构相似性，式(4.4)，(4.5)，(4.6)中， $I\left(x,y\right)$ 表示图像亮度， $c\left(x,y\right)$ 表示图像间的对比度， $l\left(x,y\right)$ 表示图像结构。 $\alpha ,\beta ,\gamma$ 一般取1， ${\mu }_x$ 与 ${\mu }_y$ 表示两图像的均值， ${\sigma }_x$ 和 ${\sigma }_y$ 表示两图像的方差， ${\sigma }_x{\sigma }_y$ 表示两幅图像之间的协方差值，其中 $C_1,C_2,C_3$ 一般都为常数。SSIM的值与图像相似度之间成正比，SSIM越大，两图像越接近。

4.3. 网络训练的参数设置

本文网络模型的训练参数为：损失函数为Huber Loss，学习率为1e⁻³。一共训练了400轮，保证了最终的训练效果。

4.4. 实验结果与分析

为保证实验的客观，本文所做实验均采用测试对比均采用同一实验环境，同一参数设置。星系图质量的评价指标为峰值信噪比与结果相似性。

表1中的对比数据为本文模型主波束校正与传统方法主波束校正后的图像的PSNR与SSIM指标，从表中可以看出，本文所采用的深度学习的模型相比与传统图像域主波束校正方法在峰值信噪比和结构相似性分别提升了3.3294570178528与0.016697511877989957。

Table 1. Evaluation index parameters of two main beam correction methods

表1. 两种主波束校正方法的评价指标参数

本文方法与传统图像域校正方法结果如图7，图8所示。

Figure 7. Observation model (left); Observations data (with primary beam effect, after deconvolution) (centre); Corrected image (right)

图7. 观测模型(左)；观测数据(含主波束效应，反卷积后) (中)；校正后图像(右)

Figure 8. (Left) Observation model; (centre) Observation data (with primary beam model, after deconvolution); (right) Corrected image

图8. (左)观测模型；(中)观测数据(含主波束模型，反卷积后)；(右)校正后图像

因为主波束与频率相关，且随着频率的增加，波束宽度会更窄，为了更深层次分析不同频率对主波束校正的影响，本文分析了4 GHz，6 GHz，8 GHz 3种频率下的主波束。3种频率下主波束形状的变化如图9所示。三种频率的FWHM (full width at half maxima)值如图10所示。

Figure 9. Variation of primary beam shape at 3 frequencies (left) 4 GHz (centre) 6 GHz (right) 8 GHz

图9. 3种频率下主波束形状变化(左) 4 GHz (中) 6 GHz (右) 8 GHz

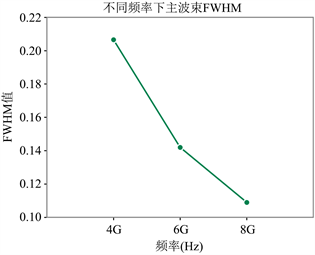
Figure 10. The FWHM of primary beam at 3 frequencies

图10. 3种频率下的主波束的FWHM

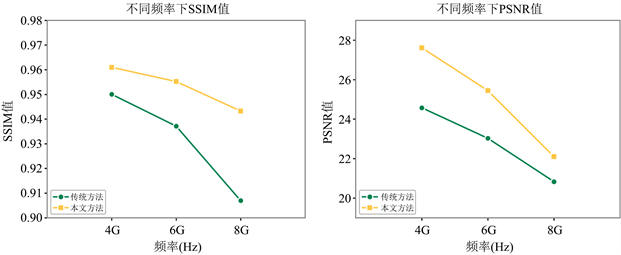
Figure 11. The comparison value of SSIM and PSNR at 3 frequencies

图11. 3种频率下SSIM与PSNR值对比

本文针对4 GHz，6 GHz，8 GHz共3个频段观测得到3种数据，然后分别使用本文深度学习方法与传统主波束校正方法进行校正。结果如图11所示，可以发现观测频率的增加的情况下，本文与传统校正方法效果都会有一定程度的下滑趋势，但校正效果方面，本文方法相对较传统方法还是表现出了一定的优势。

5. 结论

本文基于深度学习语义分割网络PSPnet进行改进，增添了残差连接与混合注意力模块CBAM，进行了不同尺寸特征融合，提出了CF-PSPnet，较传统图像域的主波束校正方法能够实现对主波束增益效应更好的校正。尤其是对于高频率中传统主波束校正方法会增加噪声的缺点，本文模型进行了出色的解决。不过本文模型也存在不足，即远离相位中心的边缘区域，图像的细节与亮度恢复的并不理想，我们后续也会继续优化模型的架构，来对这一不足进行改善。

基金项目

国家自然科学基金(12273007，11963003)，贵州省优秀青年科技人才计划项目(黔科合平台人才-YQK [2023] 006)，贵州省基础研究(自然科学)项目(黔科合基础-ZK [2022]一般143)，贵州大学培育项目(贵大培育[2020] 76号)。

参考文献

NOTES

^*通讯作者Email: [e-mail]