1. 引言
钪是我国战略性矿产资源之一,其在火箭、导弹、激光以及超导体等诸多尖端领域有广泛的应用 [1] 。钪的谱线数据被越来越多的天文学家用来分析恒星光谱 [2] 。高离化态原子离子的结构及光谱是许多现代技术的基础,也对离子高精度计算提出了更高的要求。刘鑫等人计算了类Li的ScXIX里德堡原子结构 [3] 。类He的Sc离子的研究有很多,其中绝大部分都是以等电子序列的形式给出的,其中以Głowacki的研究最为完整 [4] 。国内也进行了相关的研究,西北师范大学学者对类He的K壳层双跃迁进行了详细的研究 [5] 。最近,Nguyen等人采用Welton势对类He的自能进行了研究 [6] 。
本文研究的Kα线即2p-1s之间的跃迁谱线系,其准确数据在天体物理和等离子体物理有很重要的地位。但钪的Kα线光谱数据极少,因此需要进行系统的计算,并进行详细讨论。本文采用多组态Dirac-Fock理论(MCDF)方法来进行计算,这些数据可以为钪离子的能级寿命、布居数以及跃迁参数提供参考。
2. 理论计算方法
本文采用经典的MCDF方法 [7] ,方法内容很多,这里给出核心部分。在MCDF方法中,假设所讨论的原子或者离子体系的核电荷数为Z,电子数为N,则其Dirac-Coulomb哈密顿量为(原子单位)可以表示为
(1)
其中
是第i个电子的Dirac哈密顿量,可用下列式子表示
(2)
这里的
为核势场,α和β分别代表Dirac矢量和标量矩阵,
是其中第i个电子的动量算符,c是真空中光速。
考虑中心场近似,则可以把单电子的波函数表示为
(3)
式中κ为Dirac量子数,Pnk(r)和Qnk(r)分别为相对论径向波函数的大小分量,xkm为自旋函数。
N电子体系的组态波函数
是所有单电子旋–轨波函数组成的N阶Slater行列式波函数
的线性组合,即
(4)
在MCDF方法中,任一原子态α的波函数
由具有相同P,J和M量子数的组态波函数,
线性组合而成,即
(5)
式中nc是组态波函数的个数,Cr(α)为组态混合系数。
对(5)式子进行对角化,可以求出能级能量。在本计算中的,其他高阶修正,例如Breit修正、真空极化和自能则看作微扰。
3. 结果与讨论

Table 1. Comparisons of He-like Sc transition wavelengths (nm)
表1. He-like Sc跃迁波长的比较(nm)

Table 2. Comparisons of energy levels for 1s2p (eV)
表2. 1s2p能级值比较(eV)

Figure 1. The energy level diagram for Sc XX through Sc XII
图1. Sc XX 到Sc XII的能级图
表1给出了类氦的跃迁波长,同时也列出了实验波长,通过对比两者之间的差异,来检验计算结果
的可靠性和准确性。其中
表示百分比差异,λA为本文给出的理论计算值,λB为实验
值 [8] 。由表1可得,当前理论计算值与实验值的最大差异为0.00016 nm,最大百分比差异为0.06%,计算值与实验值相契合。再通过将1s2p能级的计算值与实验值 [9] 相对比(表2),来进一步说明当前理论计算值的准确性。其中,百分比差异公式与表1公式相同。由表2可得,计算值与实验值的最大差异不超过0.554 eV,最大百分比差异不超过0.013%。根据以上,可以得出该计算方法为真实有效的。图1给出了从Sc XX到Sc XII的能级图,当前计算的能级值范围为4111~4315 eV。表3给出了增加电子数得到的类氦到类纳的Kα跃迁参数。

Table 3. Transition parameters for Sc XX through Sc XII
表3. Sc XX到Sc XII的Kα X跃迁参数
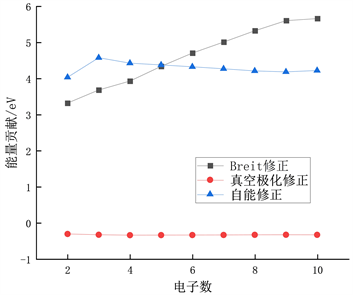
Figure 2. The contribution from high-order corrections Kα initial configurations of Sc XX through Sc XII
图2. 从Sc XX到Sc XII,高阶修正对Kα线初态精细结构能级的贡献
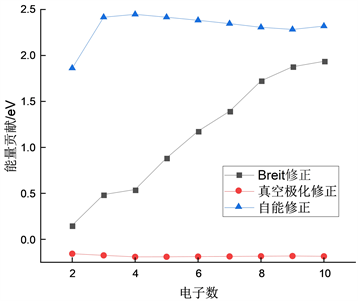
Figure 3. The contribution from high-order corrections to Kα final configurations of Sc XX through Sc XII
图3. 从Sc XX到Sc XII,高阶修正Kα线末态精细结构能级的贡献
图2和图3,讨论了高阶修正(Breit修正、真空极化和自能)对于初态和末态能级的影响。从Sc XX到Sc XII初态,考虑Breit修正对电子数目的影响,从2电子增加到10电子时,其修正值从3.3184 eV增加到了5.6603 eV,增长了2.3419 eV。而真空极化修正值处于−0.3467 ev~−0.3134 eV区间,变化较小。自能修正则从2电子时的4.0335 eV急剧增长到3电子时的4.5751 eV,随后缓慢下降到9电子时的4.1840 eV,在10电子时略微上升到4.2209 eV。考虑末态,Breit修正0.1522 eV持续增加到1.9358 eV,增长了1.7836 eV;真空极化修正最小值为−0.1912 eV,最大值为−0.1568 eV,波动较小。自能修正从1.8617 eV增到2.4257 eV,随后缓慢下降。从以上数据及图2图3可以看出,Breit修正随电子数的增加而不断增长,真空极化修正趋于不变,自能修正在初期会迅猛增长,随后趋于不变。将图2图3进行对比,初态较末态Breit修正及自能修正变化范围更大,真空极化修正较小。
4. 结语
本文采用MCDF方法详细计算了类氦到类纳钪跃迁的跃迁参数。并在计算中考虑了Breit修正、自能修正和真空极化的能级的影响。将计算值与已有的实验结果进行对比,偏差不到0.06%,与实验值非常吻合。这些数据对于填补和丰富原子结构数据库有着非常重要的意义,也能够为其他理论计算结果和实验结果提供参考。
基金项目
2022年度江苏省高校“青蓝工程”中青年学术带头人培养对象资助项目。
参考文献