1. 引言
根据国家统计局数据统计,2021年我国65岁及以上老年人口数量为2.10亿,占总人口的14.9%,其中失能老人数量众多 [1] 。根据国家统计局数据统计,2021年我国65岁及以上老年人口数量为2.10亿,占总人口的14.9%,其中失能老人数量众多并仍在增长 [2] 。调查显示,多数失能老人在洗浴过程中遇到极大不便,同时护理人员的短缺使得洗浴护理工作负担过大 [3] 。因此,研发面向失能老人的洗浴机器人对于减轻护理人员工作量具有重要意义 [4] [5] 。
目前,国内外许多学者对辅助洗浴机器人的执行机构与人体接触擦洗的方式进行了研究。Dometios等人提出了一种基于在线点云的洗浴机器人末端执行器实时运动规划 [6] ,该方法通过导航函数来调整在二维空间中预定义的擦洗路径,以使其垂直于人体表面方向上的距离得到调整,然而该方法并不能达到区域的精确擦洗。李林锋设计的个人卫生机器人辅助老人以站立姿态进行洗浴 [7] ,搓澡机构由伺服电机驱动多个搓澡头做上下往复运动,但并不能调整角度与身体表面进行贴合,擦洗的效果有待验证。陈雅设计出一种通过滑块上的电机驱动,使得沐浴海绵通过弹性绳紧贴人体皮肤表面进行接触性擦洗的洗浴机器人系统 [8] ,其能够去除人体表面油脂污渍并从效果来看比无擦洗方式洗浴效果更好,但是此种擦洗方式的精度和舒适度都无法保证。Dometios等提出一种将视觉感知和CC-DMP相融合的运动规划方法 [9] ,该方法能够在完成洗浴机器人末端执行器路径规划的同时配有专业化的擦洗动作以提高舒适性,但面对不同的人体表面结构时无法做到精准擦洗。Huang等 [10] 研发了一种利用深度摄像头和软触觉传感器跟踪人体轮廓的机器人洗浴擦洗系统,擦洗过程中末端执行器与人体始终保持一定压力相接触,但末端没有配备具有柔顺性的擦洗材料且无法达到对人体复杂轮廓区域进行擦洗。由此可见,虽然这些研究都基于接触式实现了擦洗运动,但是没有针对人体复杂的轮廓结构进行擦洗,因此,需要开发一种能够保证擦洗精度的辅助洗浴机器人擦洗控制方式。
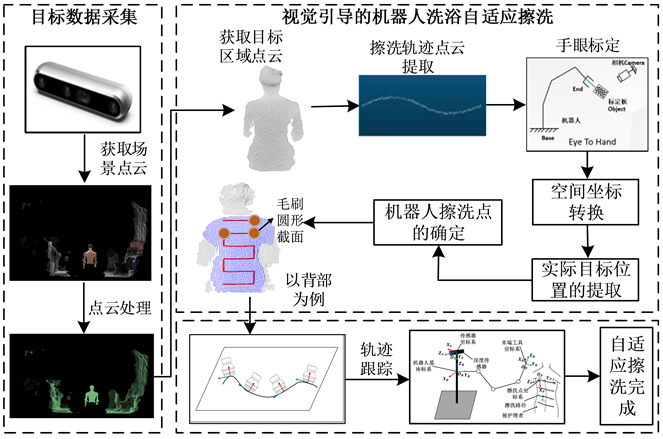
Figure 1. Scrubbing process of the robot
图1. 辅助洗浴机器人工作过程
为此,本研究提出了洗浴场景下基于视觉信息的面向人体表面特征的机械臂擦洗路径规划,深度相机获取擦洗位置,在无需构建人体三维模型的情况下直接生成擦洗轨迹,提出了自适应人体表面的末端姿态更新算法并以背部为区域进行了实际实验,最终达到机器人精准擦洗的要求。
2. 辅助洗浴机器人的总体设计与系统介绍
辅助洗浴机器人系统主要由深度相机、擦洗装置和洗浴椅以及外围的洗浴舱组成。擦洗装置为6自由度机械臂和末端执行器,机械臂能够带动末端执行器实现多自由度运动,末端执行器为固定在转盘上的柔软毛刷,电机驱动转盘带动毛刷旋转实现擦洗动作。洗浴仓内装有多角度喷淋头,可配合机器人完成人体整个区域的擦洗。深度相机获取人体表面点云信息后,擦洗工具对轨迹点进行跟踪,使柔性的毛刷能够以一定压力作用于人体表面,遍历所有擦洗点最终完成整个区域的擦洗。辅助洗浴机器人的工作过程如图1所示。
擦洗过程中末端执行器的有效清洁面为毛刷受压变形后与人体接触面积,毛刷移动形成具有一定宽度的条形清洗区域。为使清洗区域能尽可能全面覆盖所有位置以及达到精准擦洗的效果,需要自适应于人体表面凹凸特征进行擦洗路径跟踪控制。
一般情况下,被护理者的常规坐姿可分为正坐式、侧卧式和仰卧式三种 [11] 。本文的辅助洗浴机器人主要辅助失能老人对难以自行洗浴的区域擦洗,正坐时人体表面能够更好地被相机识别且便于机器人擦洗,因此选择正坐式姿势。为了保证失能老人正坐且保持位姿,我们设计了一款带有绑带且后背镂空托板的专用洗浴椅并安装在洗浴仓中。由于深度相机是固定安装在机械臂基座,为了保证洗浴者全身能被擦洗到,因此专用洗浴椅能够自主旋转,配合机器人及相机完成识别到擦洗的过程。通过分析机械臂的工作空间及常规成年坐姿下身体尺寸,机械臂能够完成表面区域的擦洗任务。辅助洗浴机器人系统设计如图2所示。

Figure 2. Intelligent assisted bathing robot system
图2. 智能辅助洗浴机器人系统设计
对于人体表面,曲面上各点的法线方向会随着曲率的变化而变化,为达到精准擦洗的效果,因此在擦洗过程中需调整擦洗工具轴向方向与接触面法向方向一致。
3. 机器人擦洗任务引导
3.1. 机器人手眼标定
深度相机被固定在机器人的基座支架上,形成了所谓的Eye-to-Hand机器人视觉系统。为了将检测到的目标空间坐标转换到机器人的基座标系,必须对机器人进行手眼标定。手眼标定的目的是找出深度相机坐标系与机器人末端坐标系之间的转换关系。在执行手眼标定的过程中,我们需要机器人处于两种不同的位姿,然后通过以下公式来确定:
其中:
其中
为相机坐标与末端的位姿转换矩阵,
和
为机器人两种不同的位姿矩阵;
和
为机器人两种不同位姿下对应的相机外参数矩阵。手眼标定求解化解为齐次方程AX = XB求解问题,其中
,
,
,计算手眼标定结果X为所求。
3.2. 擦洗轨迹点的选择与计算
3.2.1. 点云数据的曲线拟合
考虑到传感器不可避免的误差,测量的数据仍会在X-Y-Z方向上有一定的抖动,因此对原始数据进行中位值滤波。为形成一条平滑、顺畅的擦洗路径。本文使用非均匀三次B样条曲线插补算法对擦洗路径插补拟合,B样条曲线是一种基于贝塞尔曲线理论而发展起来的曲线类型,其强大的曲线拟合能力和良好的几何特性使其在机器人轨迹拟合与离散化等领域得到了广泛的应用 [12] 。我们使用擦洗路径上的擦洗点坐标作为样条曲线的型值点坐标
进行插补,相邻两数据点的x方向距离为点距s。
给定次数k后,定义了一条关于参数u的k次B样条曲线,其函数p(u)可表示为:
(1)
(2)
U表示节点向量,其中,
控制点为dj坐标
为,Nj,k(u)表示第j个k次B样条基函数,其可以用(xi)表示为:
(3)
当对擦洗曲线进行数值离散时,采用微小线段近似等弧长逼近曲线的方法以保证每个插补点都精确地位于样条曲线上,从而避免累积误差。使用deBoor公式可以求出B样条曲线在某一参数u处的一阶导数 [13] ,从而可以计算每个插补周期内参数u的增量Δu。曲线上对应一点p(u)对于u的导数为:
(4)
本文中,
为插补点的坐标值,以步长近似弧长得:
(5)
式中,
表示第i个插补步长对应参数的增量(
);l为插补步长。第i个插补点对应的u值为:
(6)
最终根据相机采集的擦洗点进行三次非均匀B样条插值拟合,得到背部全部擦洗点插补后的擦洗轨迹点如图3所示。针对上述理论,分析插补前后的轨迹点位置关系,插补点相对于原擦洗点对同一变量x值的y偏移量记为误差值。图4为插补误差,最大误差集中在擦洗点处且在±0.3 m以内,由于擦洗末端有着10 mm的可调节范围,所以此误差基本无影响。
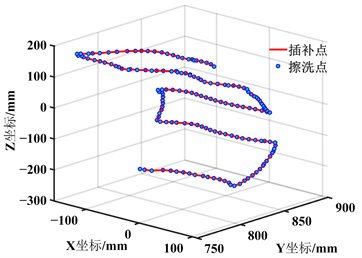
Figure 3. The scrubbing trajectory after fitting
图3. 拟合后的擦洗轨迹
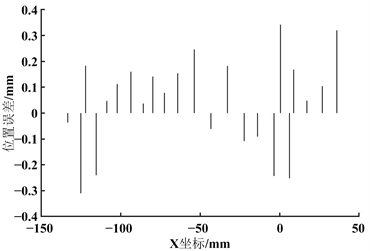
Figure 4. Trajectory error in y-direction before and after interpolation
图4. 插补前后y方向上轨迹误差
3.2.2. 擦洗轨迹点的法向量计算
由功能分析可知需调整末端工具轴向方向与接触面法向方向一致,因此人体表面的法向量估计是精准擦洗实现的前提之一。目前已有的法向量的估计方法可以分为三种类型:基于主成分分析(PCA)的方法、基于三角剖分的对偶关系算法的方法和基于稳健性统计的方法 [14] 。
本部分运用了一种基于扫描线的策略,并借助近似三角形剖分对偶关系法来建立点云间的拓扑联系。在擦洗路径中,图5所示展示了各点之间的拓扑关系和三角形划分。通过这些划分生成三角网格后,可以计算每个三角面片的法向量,并将这些法向量近似作为相应顶点的法向量。
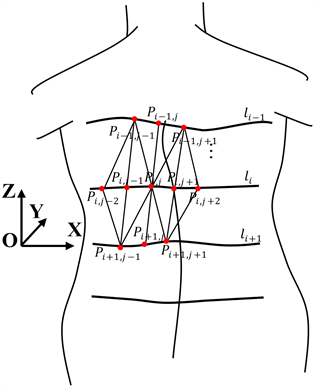
Figure 5. Topological relationship between location points
图5. 位置点拓扑关系
设擦洗路径集合
,各路径擦洗点为子集
。取当前擦洗点Pi,j,搜索位置集合P,得到与Pi,j位于同一条扫描线上的Pi,j−1和Pi,j+1,以及相邻两条扫描线上距离Pi,j最近的Pi−1,j和Pi+1,j,则得到分别以{Pi,j, Pi,j+1, Pi−1,j}、{Pi,j, Pi−1,j, Pi,j−1}、{Pi,j, Pi+1,j, Pi,j+1}为顶点的四个三角形,调整顶点的顺序,使其满足右手定则。
给定三角形的三个顶点坐标分别为
,
,
,那么可以通过一个公式计算出这个三角形的法向量。
(7)
(8)
(9)
利用(7)~(9)式计算四个三角形的法向量分别为n1、n2、n3、n4。对共顶点Pi,j,以各个三角形的面积作为权系数,计算这些法向量的加权平均值,并将结果近似作为该点的法向量
。
按上述算法遍历所有点,即
且
,则对于所有点计算其法向量,若为擦洗点Pi,j边界上的点则以其共顶点的两个相邻三角形的法向量进行加权平均,得出该点的法向量。最后对背部曲面上擦洗点求取法矢量,如图6所示。
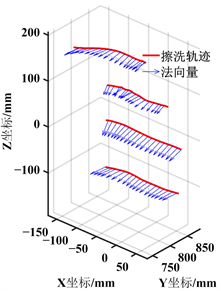
Figure 6. Normal vector estimation for scrubbed surfaces
图6. 擦洗曲面法矢量估计
4. 擦洗轨迹规划
4.1. 实时轨迹规划方法
对于图7所示的擦洗曲线,通常可以通过外部传感器获取轨迹上若干个型值点的坐标值,作为轨迹规划的型值点。然而当擦洗路径较长时,型值点和插补点数量也会随之增加。如果对所有的点采用曲线同时拟合,无疑会增大上位机性能负担,导致计算过慢甚至超出上位机计算能力而无法的得到准确的轨迹。本文提出的轨迹规划与实时控制方法如图8所示。
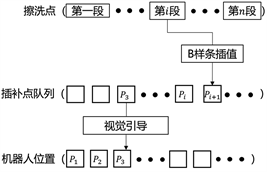
Figure 8. Interpolation point first in, first out queue
图8. 插补点先入先出队列
为了解决这一问题,本文采用一种分段式插补方法,按照一定段长将擦洗轨迹从起点到终点分成若干段,每段包含一定数量型值点。依次对各段擦洗轨迹进行插补并将插补点存入一个先入先出队列,如图所示,控制函数从队列头部开始读取并调用插补点来引导机器人末端运动,B样条插补与实时引导分别位于两个不同线程,两者可以同步进行。所以本方法不必等所有点的插补完成再进行运动控制,只需第一段插补后即可开始运动。
4.2. 机器人工作位姿优化策略
以图9为参考,在擦洗点Pj处建立工具坐标系{H}PIJK,然后使用该坐标系和基坐标系{B}OXYZ之间的相对关系来确定擦洗装置在基座标系上的位置和姿态。此过程涉及到擦洗点处曲面法向量沿X、Y、Z方向分量大小的定义,即ax、ay、az。

Figure 9. Schematic of the scrubbing pose
图9. 擦洗位姿示意图
若定义Pj点处擦洗工具位姿为
,擦洗头矢量
,计算出I轴、J可得到毛刷的姿态,令I轴正方向为擦洗点Pj的切线方向,切向矢量
,J 为K与I的叉积 [15] ,记为
,则由I、J、K构成的工具坐标系相对于机器人基座标系的转换矩阵
可表示为:
(10)
式
为该擦洗点对应的擦洗工具接触点。将擦洗位置转换成机器人末端位姿,各坐标系转换关系为:
(11)
式
描述了机器人进行擦洗操作时所使用的位姿矩阵,
为擦洗工具坐标系相对于擦洗点局部坐标系的转换矩阵,
为工具坐标系相对于末端法兰坐标系的转换矩阵。在擦洗过程中,工具坐标系和擦洗点的局部坐标系重合,即
,I为单位矩阵,d为工具长度且d = 10 cm,因此工具坐标系{H}相对于末端法兰坐标系{E}的变换矩阵为:
(14)
擦洗工具中心位置表示为:
(15)
因此机器人的位姿矩阵可表示为:
(14)
(15)
其中Γ−1为机器人的逆运动学模型,串联各擦洗点即可完成完整的机器人擦洗轨迹。实际工作中,擦洗工具的姿态变化是工具坐标系绕基座标系XYZ 各轴旋转得到。构成的复合转动矩阵
为:
(16)
式中
(17)
其中atan2 是双变量反正切函数。实际上在擦洗工具运动过程中,擦洗工具的中心轴线是K轴,与擦洗位置点的Y轴同向,所以擦洗工具局部坐标系与擦洗点坐标系相对姿态的关系就是确定好K 轴的情况下,IJ轴自转角度
的调整。通过轨迹上的位置点集
计算相邻点构成的向量
、
夹角
,即末端擦洗工具在基座标系下的旋转角度
。为减小控制器计算量,设定轮廓阈值
,若
,则不调整擦洗工具位姿。其中
计算公式为:
(18)

Figure 10. Figure of changes in back contour angle
图10. 背部轮廓角变化图
对脊椎下方的擦洗轨迹计算向量夹角
后得出如图10的变化曲线,其中多数轮廓变化角不是很大,例如第三个位置点对应实际假人背部的相应位置,发现其轮廓基本为平坦的,通过多次数据采集取定阈值角
为5˚,即轮廓变化角度小于此角度的末端无需调整姿态,大大降低了算法的复杂度。
利用上述方法计算各擦洗点的位姿,将得到关节角通过编程语言输入到六轴机械臂控制器中,实现最终擦洗控制。
5. 轨迹规划擦洗实验验证
5.1. 实验设计
为验证算法鲁棒性和实际效果,选用假人背部作为擦洗对象,初步搭建了实验系统,试验平台主要由睿尔曼RM-65机械臂、上位机以及末端软毛刷及洗浴椅等组成,机器人重复定位精度为±0.05 mm,上位机程序在VisualStudio上运行,点云处理基于PCL开发,实时数据传输基于socket连接。
5.2. 实验结果及分析
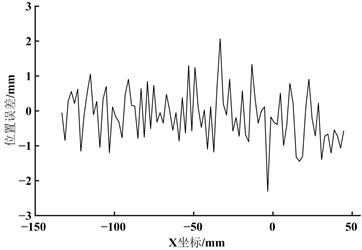
Figure 11. Displacement fluctuation in the Y direction during scrubbing
图11. 洗涤过程中Y方向上的位移误差波动
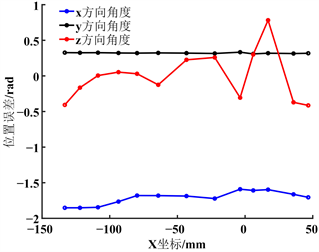
Figure 12. Change in posture angle of cleaning tools
图12. 擦洗工具姿态角度变化
本文沿末端x方向以点距2 mm对擦洗曲线采样,对擦洗过程中末端擦洗工具实际运动与期望轨迹的误差进行分析,采集得到末端轨迹在y轴方向的轨迹误差,如图11所示,图中误差最大值为−2.23 mm,由于擦洗毛刷可调节长度为10 mm,擦洗装置的中心点在毛刷中间,误差值在此范围内,所以此误差对于擦洗过程与人体皮肤表面的贴合度几乎没有影响。同时对机器人擦洗过程中的末端姿态数据进行采集,
变化曲线如图12所示,实验中对位姿更新轮廓角度设置了阈值,从图中看出ry数值几乎没有变化,只是rx、rz发生变化,这与理论的擦洗位姿更新策略一致。机器人在擦洗运动中,机器人各关节角序列变化如图13所示,曲线变化平滑无突变。

Figure 13. Changes in robot joint angle during scrubbing process
图13. 擦洗过程中机器人关节角度变化
5.3. 运行时间
为了验证本文方法的优势,将本文提出的分段式实时控制方法所需的时间与非实时时间进行对比,如表1所示,实验结果表明使用了分段式实时控制的策略之后完成目标擦洗轨迹规划所需要的时间更短,效率更高。
6. 结论
本文提出了一种辅助洗浴机器人实时轨迹规划擦洗控制方法,使用非均匀三次B样条对点云轨迹进行插补,在完成第一段轨迹采集、插补和法向量计算后控制机器人运动,该方法与依次执行程序比较具有更高的实时性,将整个轨迹规划时间缩短至60 s以内,在提高擦洗轨迹规划实时性的同时保证了擦洗质量。
采用三次B样条进行插补共取241个插补点,插补误差在每个擦洗点处,最大误差为±0.3 mm以内,满足末端擦洗毛刷的可变形长度,因此无影响。计算人体表面轮廓轨迹所在的法向量并结合轮廓阈值保证擦洗装置始终垂直于轨迹的局部表面,运动中末端姿态的变化验证了位姿更新策略,保证了机械臂擦洗的精准性。
对擦洗运动中的关节电机角度进行采集,机器人运动平滑,末端得到反馈位置坐标的误差不超过2.23 mm,在可调节范围内。为了提高机器人擦洗的真实性和舒适度,在擦洗过程中加入接触力的调节将在后续工作中做进一步研究。
基金项目
本项目(项目名称:失能老人智能照护机器人系统关键技术及产品研发)受到国家重点研发计划项目(2022YFC3601403)支持。
参考文献
NOTES
*通讯作者。