1. 暗物质和牛顿修正动力学学说(MOND)
暗物质 [1] 是理论上提出的可能存在于宇宙中的一种不可见的物质。大量天文学观测中发现的疑似违反牛顿万有引力的现象可以在假设暗物质存在的前提下得到很好的解释。天文学家卡普坦于1922年提出可以通过星体系统的运动间接推断出星体周围可能存在的不可见物质。1933年,天体物理学家兹威基利用光谱红移测量了后发座星系团中各个星系相对于星系团的运动速度。利用位力定理,他发现星系团中星系的速度弥散度太高,仅靠星系团中可见星系的质量产生的引力是无法将其束缚在星系团内的,因此星系团中应该存在大量的暗物质。史密斯在1936年对室女座星系团的观测也支持这一结论。1939年,天文学家巴布科克通过仙女座大星云的光谱研究,显示星系外围的区域中星体的旋转运动速度远比通过开普勒定律预期的要大,对应于较大的质光比。1940年奥尔特对星系外围区域星体运动速度的研究,指出其总质光比可达250。1959年凯恩和沃特研究了彼此吸引的仙女座大星云和银河系之间的相对运动,通过相互它们靠近的速度和彼此间的距离,推论出我们人类所处的本星系团中的暗物质比可见物质的质量约大十倍。1970年鲁宾和福特对仙女座大星云中星体旋转速度做了研究,利用高精度的光谱测量技术,他们可以探测到远离星系核区域的外围星体绕星系旋转速度和距离的关系。按照牛顿万有引力定律,如果星系的质量主要集中在星系核区的可见星体上,星系外围的星体的速度将随着距离而减小。但观测结果表明在相当大的范围内星系外围星体的速度是恒定的。1973年罗伯兹和罗兹运用21厘米特征谱线观测技术探测仙女座大星云外围气体的速度分布,也从另一角度证实了这一结论。1980年后,出现了一大批支持暗物质存在的新观测数据,包括观测背景星系团时的引力透镜效应,星系和星团中炽热气体的温度分布,以及宇宙微波背景辐射的各向异性等。星系旋转曲线描述了漩涡星系中可见天体的环绕速度和其距离星系中心距离的关系。根据对漩涡星系中可见天体质量分布的观测以及万有引力定律的计算,靠外围的天体绕星系中心旋转的运动速度应当比靠中心的天体更慢。然而对大量漩涡星系旋转曲线的测量表明,外围天体的运行速度与内部天体近乎相同,远高于预期。这暗示着这些星系中存在着质量巨大的不可见的物质。结合位力定理,可以通过星系中可见天体的弥散速度分布计算出星系中的物质分布。这种方法同样适用于测量椭圆星系和球状星团的物质分布。结果表明,除个别以外,大部分星系和星团的物质分布都与观测到的可见物质的分布不符。通过暗物质的提出历史可以看出暗物质的实质是星系的旋转速度与万有定律计算的结果不符,按照经典万有定律推算,距离星系的中心越远,星系的旋转速度应该越慢,而观测结果显示星系旋转速度基本是恒定的,现在对形成这个现象的主流解释是宇宙空间存在大量的暗物质。
暗物质研究的最直接办法就是探测暗物质粒子 [2] [3] [4] [5] ,欧洲大型强子对撞机和所有的加速器实验还没有发现暗物质粒子的迹象。地下直接探测实验国际上已进行了数十年。中意合作DAMA实验发现了时间调制现象,该现象可以解释地球绕太阳公转的原因。2009年12月18日,CDMS地下实验项目组宣布,所发现的2个事件可能与暗物质粒子有关。CDMS所用的探测器被埋在美国明尼苏达深达700米的地下,周围的岩石、塑料、铅、铜和其他物质被用来阻止除了暗物质之外的正常微粒到达探测器,这样可能与暗物质相混淆的宇宙射线和其他粒子就被排除在外了。目前国际上大约有几十个科学小组在设计实验以期发现暗物质接近普通物质原子的那一刻产生的信号,其中XENON100的实验是灵敏度最高的,但公布的最新观测结果是没有发现暗物质粒子存在的迹象。最新空间间接探测试验结果主要来自于FERMI伽马射线望远镜,PAMELA空间探测器,ATIC南极气球实验等。2009年3月FERMI卫星公布其一年半的观测数据,经伽马射线谱线探测,背景分布方面没有探测到任何明显信号与暗物质粒子有关。另外在电子观测方面ATIC、PAMELA、FERMI、HESS几个探测器发现电子观测数据与理论模型相比都存在“超”,但“超”的大小并不一致。反质子观测方面,PAMELA上天3年,观测到的反质子能谱基本与宇宙线次级能谱吻合很好,没有探测到异常特征。自上世纪80年代以来,人们进行了许多暗物质探测实验,但迄今还未能探测到暗物质。
天文学家对观测到的与牛顿定律不符的另一个解释是牛顿修正动力学学说(MOND) [6] [7] [8] ,1983年由米尔格龙提出的经修改的牛顿动力学是在微小的加速度尺度——大约为10−10 m/sL上巧妙地修改了牛顿定律。他假定当万有引力的强度(重力加速度的大小)比较大时,物体受到的引力可以用牛顿万有引力的公式描述,但是当其减弱到一定程度时,则偏离标准的牛顿动力学。具体地说,我们所熟悉的物体运动定律是牛顿第二运动定律F = ma,即物体加速度乘以质量等于力。他把这一定律改为
(1)
这里a0是一个理论中的新常数,修正因子μ(a/a0)是a/a0的一个函数,满足
,
。也就是说,在较大的重力加速度下这个修正因子趋于一个常数,与平常的牛顿定律一致。但当重力加速度减小到一定程度时,加速度与力之间就有一个更复杂的关系。有了这一修正因子,就可以得到
(2)
这里aN是按牛顿万有引力公式算出的引力加速度,而a则是米尔格罗姆理论给出的加速度。代入圆周运动的加速度为a = v2/r,就得到
或
(3)
即在远离中心处旋转速度趋于常数。根据对星系的观测,可得到上式中加速度常数的数值约为a0 ≈ 1.2 × 10−8 cms−2。2002年,另一位以色列物理学家贝肯斯坦构造出了一种既满足相对论、又能产生MOND行为的理论。在广义相对论中,描写时空弯曲的是所谓度规张量,而在这一理论中,引入了一个新的张量场、一个矢量场、一个标量场,以及一个辅助(非动力)标量场,通常的时空度规张量则由这几个量共同决定,因此被简称为张量–矢量–标量(TeVeS)理论,但是这个理论由于引入了多种场,其复杂程度超过一般的暗物质模型。后来,两位捷克科学院的理论物理学家康斯坦丁斯·斯科迪斯和汤姆·兹沃什尼克,在TeVeS的基础上,又构造了一种新的理论,称之为相对论MOND (RMOND)理论。这一理论中引入了一个具有复杂的相互作用的矢量场和两个辅助标量场。还有学者提出牛顿修正动力学理论(MOND)的模型则假设来自于其他星系的引力作用会对星系外围的恒星产生干扰,改变其惯性质量,这就导致了它们比理论上的公转速度要快得多。目前的各种牛顿修正动力学学说(MOND),都还存在各种问题,不能成为一个理想的引力理论。
2. 星系旋转速度和星系的模型
星系 [9] [10] 是构成宇宙的基本单位,它包含恒星、气体、宇宙尘埃和暗物质,并且受到重力的束缚。典型的星系如图1,从只有数千万颗恒星的矮星系,到有上兆颗恒星的椭圆星系都有,它们都环绕着一个质量中心运转。除了单独的恒星和稀薄的星际物质之外,大部分的星系都有数量庞大的多星系统、星团以及各种不同的星云。在可观测宇宙中,星系的总数可能达到一千亿个(1011)以上。大部分星系直径介于1,000至10,0000秒差距,彼此之间距离则是百万秒差距的数量级。星系大小差异很大。椭圆星系直径在3300光年到49万光年之间;漩涡星系直径在1.6万光年到16万光年之间;不规则星系直径大约在6500光年到2.9万光年之间。星系的质量一般在太阳质量的100万到1兆倍之间。星系内部的恒星在运动,而星系本身也在自转,整个星系也在空间运动。最普通的是椭圆星系:它们有着椭圆形状的明亮外观;漩涡星系是圆盘的形状加上弯曲的旋涡臂;不规则星系,通常都是受到邻近的其它星系影响的结果。星系的结构可以分为三个主要部分:中心区域、盘状结构和外围区域。中心区域通常被称为星系核,它是星系中最亮的区域,包含了大量的恒星和黑洞。核心区域的形态多样,有些星系核呈现出明亮而紧凑的核球状结构,而另一些则呈现出扁平的盘状结构。盘状结构是星系中最显著的特征之一,它由大量的恒星、气体和尘埃组成。盘状结构通常呈现出旋转对称的形态,类似于一个扁平的圆盘。盘状结构可以进一步
分为两个部分:星盘和气体盘。星盘主要由恒星组成,而气体盘则主要由气体和尘埃组成。气体盘中的气体和尘埃会通过引力作用逐渐聚集形成新的恒星。
星系旋转速度曲线 [11] - [16] 是描述星系内部物质运动的曲线,它展示了星系中不同半径处物质的旋转速度。通过测量星系内不同区域的气体或恒星的旋转速度分布,我们可以绘制出星系的旋转速度曲线。上世纪70年代,人们观测了银河系和很多其它星系的旋转曲线如图2、图3,也就是到星系中心不同距离处的恒星或气体的旋转速度值。根据传统的牛顿引力理论,恒星或气体的旋转速度应该与它们受到的引力有关,星系中心的恒星密度较高,而越到边缘其恒星密度越低,再加上离中心距离更远,因此距离中心越远处受到引力应该越低,那么其旋转速度也应该越慢。但是,实际观测的结果并非如此,星系旋转曲线大多趋于一个常数,这就是所谓的“平坦旋转曲线”。甚至,人们使用射电望远镜还可以观看星系的旋转气体,在星系中这些气体的分布范围比恒星所形成的盘要大不少,因此可以看到这些气体所处的边缘已经几乎没有恒星了,而且这些气体本身的量也不多,按理说这里的引力应该下降了,但是这些气体的转速仍然未见下降。
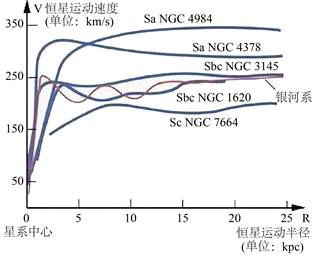
Figure 2. Rotation velocity curve of neighboring galaxies 1
图2. 临近星系的旋转速度曲线1
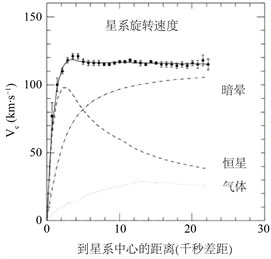
Figure 3. Rotation velocity curve of neighboring galaxies 2
图3. 临近星系的旋转速度曲线2
3. 偏转引力理论和修正引力公式下的星系旋转速度
3.1. 偏转引力理论简介
偏转引力理论 [17] [18] [19] 认为质量的基本单位为核子(质子、中子的统称),每个核子单位时间都发出大量引力子,对于星球,星球内部的核子发出的引力子与星球内部其它核子发生作用,形成星球内部的凝聚力,星球外层的核子发出的引力子,部分发往球外并分散在星际空间,引力子在空间以引力能量波的形式传播形成引力场,当引力能量波中的引力子遇到其它星球的核子时,与其发生共振,引力子被其它核子吸收,形成引力。每个引力子都携带能量h (普朗克常数)。
偏转引力理论根据共振原理推断,引力能量波的波长λ等于核子的直径(半径为r0)。
(4)
引力能量波在空间的传输速度为光速c = 3 × 108 m,则引力能量波的频率为:
(5)
周期为
(6)
偏转引力理论认为引力能量波每个波包携带的能量为普朗克常数h,相邻两核子交换的能量就是核子的结合能 [20] ,计算两核子单位时间交换的能量,可以确定核子单位时间1 s内发出的引力子数量为:
(7)
通过对球外引力子数量的计算 [21] ,说明能够发射到球外的核子壳层厚度为:
(8)
(9)
星球发射到球外的引力子数为:
(10)
(11)
偏转引力理论认为,星球之间的引力与星球之间交换引力子的数量成正比,而球外引力子数量与星球表面积成正比,因此,星球之间的引力应该与星球的表面积成正比。对于球状星体1与球状星体2相距R时,球状星体2单位面积接收的球状星体1引力子数量为1/4πR2,因此牛顿万有定律应该修改为:
(12)
设星球1的半径为r1,星球2的半径为r2,引力公式也可以表示为:
(13)
3.2. 星系和星系中星球的引力和旋转速度
我们计算星系的旋转速度,是计算星系中可视星球的旋转速度,图4中,星球S2为我们要计算速度的可视星球,其质量为m2,半径为r2。星系一般都是扁平盘装结构,我们将星球S2以内的星系G1等效为一个高度很小的柱体,柱体的半径r1就是星系的半径,柱体的高度H就是星系的厚度。星球S2与星系中心G1的距离为R。
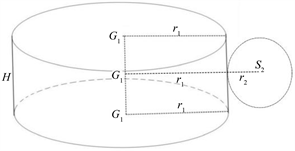
Figure 4. Schematic diagram of gravitational action in the galaxy 1
图4. 星系引力作用示意图1
对于盘状星系,可以将星系看成一个厚度为H (盘面厚度)的圆柱,相对于星系中的星球2,它的引力作用面为:
(14)
星系中我们要计算速度的球状星体2,相对于星系来说,可以看成小星球,这里我们继续用其质量m2计算引力,这样
星球S2受到星系G1之间的引力为:
(15)
星球之间的引力提供了星球绕星系旋转的向心力:
(16)
(17)
当R为0时,星系的半径r1为0,星系的盘面高度H也为0,当R增加时,由于
,r1也增加,盘面厚度H增加,当R增加到一定程度后,盘面厚度达到标准盘面厚度Hmax,随后H不在增加成为恒定值,在R增加过程中,一般的
,
,此时星系的旋转速度为恒定值:
(18)
星系盘面由0过渡到Hmax可以用公式表示:
(19)
H带入为:
(20)
公式中e为自然函数,σ为达到近似峰值的距离。
由此看出,星球的旋转速度与星系的盘面高度有关,与距离星系中心的距离无关。
3.3. 影响星系旋转速度的其他因素
3.3.1. 星系互绕的影响
星系G1对星球S2的引力使S2绕星系G1的中心旋转,同时星球2对星系1也会产生引力,使得星系G1绕星球S2旋转,只是这个力要小的多。
星系G1为圆柱面,它单位面积占星球S2距离R的面的比例为1/2πR,
(21)
星系G1受星球S2影响产生的速度为:
(22)
3.3.2. 星系剩余质量的影响
星系的质量一般服从正太分布:
(23)
这里x为星系G1的半径r1,σ为方差,取星系的最大半径为3σ,正太分布在3σ以内的质量为总质量的99%。将星系不同半径的剩余质量作为外围星系的质量,对于星球S2,其后面的外围星系会对S2产生影响,不在S2后面的其余的剩余质量对S2没有影响,图5、图6中,将星球S2后面的星系剩余质量等效为一个圆柱形星球,可以计算星球S2以外物质对星球S2旋转速度的影响。
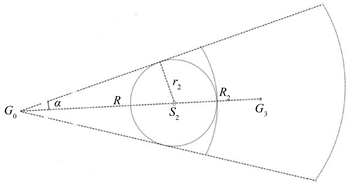
Figure 5. Schematic diagram of residual mass equivalence of galaxies
图5. 星系剩余质量等效示意图
(24)
(25)
(26)
(27)
(28)
(29)

Figure 6. Schematic diagram of the gravitational effect of the galaxy 2
图6. 星系引力作用示意图2
3.4. 星系旋转速度及其影响因素的数据模拟
星系旋转速度数据模拟见表1。这里选取了一部分表格,整体表格有一万行,读者在这个表格上续行就行。表中第一列为一些常数,rmax为星系的最大半径Rmax减去星系中需要计算速度的星球半径r2后的最大值,近似的rmax = Rmax,由图2和图3可以看出,星系盘的边沿在20~25千秒差距(kpc)之间,这里取24千秒差距,1秒差距(pc) = 3.086 × 1016 m,24千秒差距 = 7.405 × 1020 m。n为rmax的等分数,这里取10000。Δr为每等份宽度,m0为核子质量,r0为核子半径,ρmax为星球最大密度,可以认为星系中心的密度最大值就是中子星的物质密度,这里它就是核子的物质密度
,星系的物质分布一般服从正太分布,这里正太分布的y轴就是星系的中心G0,σ为正太分布的方差,这里取星系半径的最大值Rmax (rmax)为3σ,可以认为星系99%的物质都包括在星系最大值Rmax之内了。m2为星系内需要计算速度的星球,这里选这个星球的质量m2与太阳的质量相等为1.989E30 kg,选这个星球的半径r2与太阳的半径相等为6.955E8 m,这个星球的密度为ρ2与太阳的密度相等为1408 kg/m3,GS为引力公式中的系数,相当于牛顿万有定律中的引力常数G。Hmax为盘面形成后的厚度。不同星系的星系盘的厚度不一样,银河系盘面的厚度为1000光年,这里取星系盘的厚度与银河系星系盘厚度相等也为1000光年,1光年为9.4607E15 m,1000光年为9.4607E18 m。星系盘总质量为正太分布3σ以内的质量/0.99。盘高拐点为星系盘高度基本达到正常高度时对应的星系半径r1的值。
表中第2列为星系半径R,初值为每等份宽度Δr+星球2的半径r2,然后每增加一行,半径R+宽度Δr。表中第3列为星系等效半径r1,其值为R − r2,第4列为星系盘厚度,在星系盘半径为0时,星系盘厚度也为0,星系盘半径达到星系盘厚度拐点时,星系盘厚度达到正常厚度,其值符合公式19,第5列为星系相应半径下的物质密度,此值符合正太分布,由公式23乘以物质最大密度ρmax给出。第6列为不同密度层的物质质量,起始值为πC2(r1)2Hρ,第二行起不同密度环的质量,其值为
,第7列为质量和,表示不同星系半径以内物质质量的总量,此列最后一行为3σ以内星系的总质量,占整个星系质量的99%。第8列为星系等效柱体侧面积,为不同星系半径下与星球S2的引力作用面积,第9列为星球S2受到星系G1的引力,星系G1使用引力作用面积,星球S2使用质量。第10列为星球在S2在星系G1引力场中的旋转速度。
第11~13列说明星系G1受到星球S2作用力对星球S2旋转速度的影响。第11列为星系G1受到星球S2的作用力,由于星系G1在S2引力场中以圆柱侧面为引力作用面,这里只与距离R的一次方成反比,第12列为星系G1受到星球S2的引力形成的旋转速度,第13列为星球S2和星系G1运行的速度和。由第10列星球S2的速度v2和第12列星系G1受星球S2影响产生的反向速度V1可以看出,V2 ? V1,星系G1受星球S2影响产生的反向速度V1可以忽略。
第14~19列说明星系不同半径下的星系剩余质量对星系旋转速度的影响。第14列为星球S2后面等效柱状星球G3对星球S2的作用距离,考虑到rmax为星系3σ的作用范围,星系的边沿取4/3rmax,取星系剩余距离的1/3处为剩余质量的作用点,则
,第15列为在星球S2后面的剩余质量,由公式25计算。第16列为剩余质量的等效圆柱半径,这里物质密度取1408 kg/m3,第17列为星系剩余质量对星球S2的引力,由上式29计算,第18列为星球S2受到G1和G3力的合力,这里为两力只差,第19列星球S2受到F1和F3合力影响后的旋转速度,第20列为星球S2受到星系G1,星系剩余质量等效球G3和星球S2对G1影响作用,S2的速度和。由第9列F2和17列F3可以看出,星系G1对星球S2的引力F2 ? 星系剩余质量等效球G3对星球S2的引力F3,星系剩余质量等效球G3对星球S2的引力F3可以忽略。

Table 1. Digital simulation table of galaxy rotation speed
表1. 星系旋转速度数字模拟表
综上所述,星系的旋转速度主要由星系中测量星球受到测量星球以内的星系引力形成。图7是星系旋转速度的模拟效果图(V2)。

Figure 7. Simulation effect of galaxy rotation speed
图7. 星系旋转速度模拟效果图
4. 讨论
星系的结构是复杂的,上面的结论只适用于富星且星系盘360˚分布基本均匀的椭圆星系;对于存在旋臂的螺旋星系和棒旋星系,星系的旋转速度会随旋臂出现上下波动;对于透镜状星系和不规则星系应进行具体分析;对于像太阳系这样的少星星系,上面结论不适用。对于星球,由星球表面积发出的引力子趋于饱和,所以引力与星球表面积成正比,对于星系,由星系侧表面积发出的引力子远未趋于饱和,不同星系的物质密度不一样,由星系侧表面积发出的引力子饱和程度不一样,所以不同星系对物体的引力不一样,不同星系中物体的旋转速度也不一样,星系的旋转速度,除与星系盘的厚度有关外,应该与星系物质密度有关,星系盘厚度相同的星系,物质密度越大,星系的旋转速度越大;星系盘密度相同的星系,星系盘越厚,星系的旋转速度越大。星系一般都有一个球形星系核,随着球形星系核大小的不同,星系中心厚度过渡到星系盘正常厚度的情况不一样,星系旋转速度开始曲线也会不一样,这些细节有待进一步研究。本文的结论,希望广大天文工作者验证。
5. 结论
物质由核子(质子和中子的统称)构成,每个核子都发出大量的引力子,星球内部核子发出的引力子被星球内部其他核子吸收,形成星球内部的凝聚力,星球壳层的核子发出的引力子有一部分发射到球外以引力能量波的形式传播形成引力场,当引力能量波遇到引力场中其他星球的核子时,与其发生共振形成能量转移,引力子被其它核子吸收形成引力。引力由星球壳层核子发出的引力子多少决定,这个引力子多少与星球表面积成正比,因此星球的引力与星球的表面积成正比,万有引力公式中与星球质量成正比,只是一种近似。一般的星系都是盘状结构,在星系旋转速度计算中,星系中的星球受到的引力与盘状结构的侧面积相关,由修正后的引力公式和向心力公式可以得到星系的旋转速度与星系盘的厚度相关,与星系的半径无关。
式中GS为引力常数,Hmax为星系盘厚度,e为自然函数,σ为星系盘厚度达到近似峰值时的星系半径,r为测量点与星系中心的距离。经本文数据模拟,星球对星系的引力对星系旋转速度的影响可以忽略,测量点以外星系剩余质量对星系的旋转速度影响也可以忽略。经本文分析,对于特定的星系,星系旋转速度是恒定的,星系旋转速度计算中不需要暗物质的参与。
参考文献