1. 引言
随着环境污染加剧以及在“双碳”战略目标下,我国的能源结构向可再生能源转型是尤为重要的一步 [1] 。可再生能源已经成为大多数国家的能源战略的重要组成部分以及转型的核心。其中,风能和太阳能新增发电容量创下新纪录,加速了转型的进程 [2] 。国际能源署在《2022年可再生能源报告》中预测,在2022年到2027年五年中,全球的风能发电能力将翻一倍,光伏发电能力将翻两倍,两者可占可再生能源新增发电能力90%甚至更多,其中中国的增量将占全球增量的50%左右 [3] 。但是风力资源和太阳能资源都存在着随机性、波动性、不稳定性等缺陷 [4] ,造成弃风、弃光现象严重,资源浪费、利用率低等问题,不能保证其稳定发电。为了解决这些问题,单纯扩大光伏和风力发电厂的规模,将会产生巨大隐患。为了提高光伏/风力发电系统的可靠性,可以引入具有储能技术和灵活输出能力的储能系统,使系统在风、光资源匮乏时同样能够有效地调节系统发电功率。目前,各种储能技术得到了发展,如电容器、电池、飞轮、抽水蓄能、压缩空气、氢气等 [5] 。其中,储氢在储能密度和存储时间方面具有绝对优势 [6] 。此外,储氢还具有来源广、清洁无污染等优点 [7] 。
多能互补作为我国能源结构的新形态,打破了单一传统的能源模式,能源的低碳化、综合化、绿色化发展将成为解决全球气候问题、保障我国能源安全的核心动力,风–光–氢多能互补系统将会成为未来能源互联网中的重要组成部分 [8] 。研究风–光–氢系统的容量配置、优化配置、影响参数和经济性分析意义重大,容量配置过高会导致成本增加和资源浪费,而容量配置过低则会导致电力供应不足,影响居民的日常生活。因此,如何根据当地的资源条件和负荷需求配置发电厂存储单元的容量大小是目前亟需考虑的问题 [9] 。
储能容量配置优化问题是近年来研究的热点。张东等 [10] 提出了一种太阳能PV/T光储直驱热电联产系统,并通过实验测试系统性能,结果发现增加储能后减少了能源消耗,并提升系统的发电效率和综合效率。Das等 [11] 提出了一种水循环优化算法,通过净现值最小化来优化光伏/沼气/抽水蓄能/电池储能的配置。Sanajaoba等 [12] 开发了一种基于萤火虫算法的数学模型,以最小失电损失率为目标获得风/光/电池/氢储能的最佳容量。可以看出,为了解决固有非线性变量问题,如由于天气模式和负荷模式等随机变量而提出的优化问题,文献大都使用启发式算法。但在储能方式方面,文献多集中于电池储能、抽水蓄能等储能方式,较少考虑储氢技术。
基于当前可再生清洁能源和多能互补系统的现状,本文提出一个风–光–氢互补综合能源系统优化模型,采用遗传算法对系统进行优化分析。将所提出的模型应用于某风光互补发电项目,根据实地天气数据和用户负荷数据得到最优的储能装置容量。同时对系统进行能源和经济性分析,保证系统可行性。
2. 风–光–氢综合能源系统
本文研究的风光氢多能互补系统结构如图1所示。系统主要由三个子系统组成——风力涡轮机发电系统、光伏发电系统和储氢系统(包括电解槽、储氢罐和燃料电池)。当光伏发电和风电产生的电量超过电力需求时,电解槽通过电解水将多余的电量转化为氢气。反之,当系统缺电时,燃料电池启动发电,将储存的氢气转化为电能供给系统。所提出的系统运行策略如图2所示。当燃料电池依然不能满足需求时,从电网购买电力;当系统多余电量超过储氢罐最大容量时,超过的电量并入电网。
与常规风光互补发电系统相比,该系统有如下几点优势:1) 加入储能对系统负荷缺电、能量冗余等方面进行补偿和优化,进一步满足负荷及提高能源利用率;2) 根据当地的资源条件和负荷需求配置储能单元的容量大小,不影响居民日常供电的同时最大化节约成本和资源。
3. 模型建立
3.1. 风力发电系统
风力发电系统主要由风力机和涡轮发电机组成,实现风力向机械能再向电能的转换。风力发电机的实时发电量取决于发电机的特性和轮毂高度处的风速。风电机组的输出功率
计算如式所示 [13] :
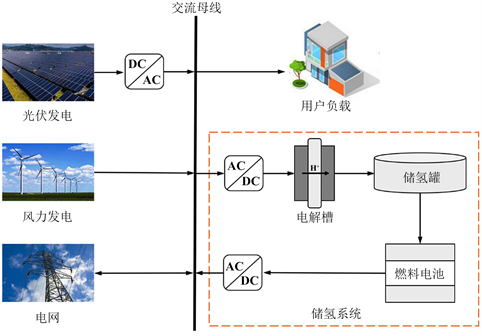
Figure 1. Structural diagram of wind-solar-hydrogen multi-energy integrated system
图1. 风–光–氢多能互补系统结构图
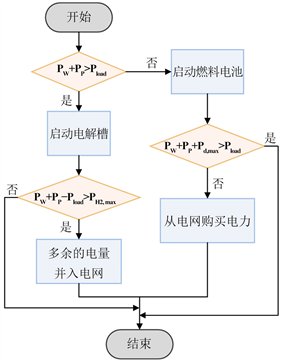
Figure 2. Operating strategy of the proposed system
图2. 系统运行策略图
(1)
式中:v是实际风速;
是切入风速;
是切出风速;
是额定风速;
是风机额定功率。
文中使用的风速数据为对应转子位于1 m处的风速,而选定的风力机转子位于70 m处,因此需用幂律方程对其风速进行修正 [14] :
(2)
式中:h是转子实际高度;
为1 m;
是时间间隔为t时转子在1 m处的风速;
是时间间隔为t时转子在70 m处的风速。风力机相关参数如表1所示 [15] 。

Table 1. Parameters of the wind turbine
表1. 风力机参数
3.2. 光伏发电模型
光伏发电系统包括光伏板、逆变器和其他电气配件。光伏发电系统的输出功率主要受到光照辐射强度、光伏板的温度和其他组件特性的影响,其输出功率
计算如下 [16] :
(3)
式中:
是光伏板的额定转化效率;
是光伏板的额定功率;A是环境下的辐射强度;
是标况下的标准辐射强度;
是温度功率系数;
是光伏板的实际温度;
是光伏板的额定温度。光伏板相关参数如表2所示 [17] 。
3.3. 储氢系统
电解槽中电解水的过程属于氧化还原反应,其中含有能量的转变和物质的消耗与生成,根据电解质的差异,将电解槽主要分为三种:碱性电解槽、固体氧化物电解槽和质子交换膜电解槽 [18] ,本文选用固体氧化物电解槽来制氢。影响电解槽的输出电压的主要因素有:输入电流、工作压力、工作温度,输出电压随输入电流的增加而增加,因而调节输入电流的大小可以控制制氢量的多少。
电解槽的阳极和阴极会分别发生以下反应:
阳级:
阴极:
氢能发电的核心是燃料电池,工作原理等价于电解水的“逆过程”,将氢能(化学能)转化为电能和热能,阳极为氢气发生氧化反应的场所,阴极为氧化剂发生还原反应的场所,再加入催化剂加速电化学反应。阳极和阴极分别发生以下反应:
阳极:
阴极:
由于质子交换膜燃料电池(PEMFC)的结构简单、启停快,具有良好的应用前景 [19] 。本文选用其来将氢能转换为电能。本文考虑了电解槽的充电效率和燃料电池的放电效率。若系统输出电量大于用户负荷,则启用电解槽制氢,储氢量为:
(4)
若系统输出电量小于用户负荷,则启用燃料电池发电,则t时刻的储氢量为:
(5)
式中:SOC为储氢罐剩余的氢体积;
为电解槽效率;
为燃料电池效率;
为t时刻风光氢系统的总输出;
为t时刻的用户用电负荷;
为每千瓦时电能产生氢气的体积;
为每立方米氢气的发电量。相关参数数值如表3所示 [9] 。

Table 3. Parameters of hydrogen storage system
表3. 光伏板参数
4. 系统优化
4.1. 目标函数
选择一种合适的优化方法对于模型求解的效率以及所得结果的可靠性起着重要作用。根据求解问题的数学模型与其所对应约束条件从而对优化方法进行划分,大致划分为线性求解算法和启发式算法两类。前者主要用于求解线性类问题,而风、光、氢多能互补系统问题的研究是一个复杂的非线性问题,因此,本文选用启发式算法进行求解。其中遗传算法因求解速度快、具有良好的全局搜索能力被许多研究者所青睐。
风光氢系统的实际输出功率与用户负荷之间的偏差大小是评判风光多能互补系统优劣的重要指标。如果只按照目标负荷给用户供电,会出现固定负荷不能满足的情况,虽然可以防止过响应的发生,但与用户的用电习惯相差太大,降低了用户的舒适度,也影响了电网的稳定性。因此,本节结合用户负荷与目标负荷之差最小作为目标函数,选取遗传算法作为优化方法,寻求系统的最优配置。目标函数的具体表达式如下所示:
(6)
(7)
式中:
为氢能发电量或者制氢功率;N为时间间隔数。
4.2. 约束条件
在该优化问题中,决策变量为:电解槽、储氢罐和燃料电池的容量。相关约束如下:
1) 风力发电输出功率约束
(8)
式中
、
为风力发电机组的最小、最大输出功率。
2) 光伏发电输出功率约束
(9)
式中
、
为光伏发电系统的最小、最大输出功率。
3) 电解槽制氢约束
(10)
式中
、
为电解槽最小、最大制氢速率。
4) 储氢罐容量约束
(11)
式中
、
为储氢罐的最小、最大容量。
5) 燃料电池容量约束
(12)
式中
、
为燃料电池的最小、最大容量。
6) 燃料电池充放电约束。
(13)
(14)
式中
、
为燃料电池的最小、最大充电功率;
、
为燃料电池的最小、最大放电功率。
7) 能量平衡约束
燃料电池充电过程:
(15)
燃料电池发电过程:
(16)
风光氢系统工作过程:
(17)
式中
为电网提供或消纳的功率。
4.3. 评价指标
为了进一步分析风光氢综合能源系统性能,本文从能源和经济两个角度对系统进行分析。采用能源增长率
作为系统能源评价指标,即加入储能后储存的能量
与未加储能的系统产出之比,表达式为:
(18)
对于经济方面,选取系统净现值(Net present value, NPV)作为评价指标。净现值表示能源系统在其生命周期内的盈利能力,只有当NPV为正时,系统才具有经济可行性。NPV的计算公式如下 [20] :
(19)
式中:i和m分别表示贴现率和设备寿命,本研究设置为8%和10年 [21] ;
表示不同储氢设备的价格;NCF(Net cash flow)为净现金流,即系统的储能发电节约的成本
与运维成本
的差值,计算如下式所示:
(20)
式中:储能发电收入
取一天内平均储能量;系统运维支出
取设备支出的6% [9] 。
5. 案例分析数据
将所提出的风光氢综合能源系统用于某风光发电项目,为其配备合适的储能容量。该多能互补能源基地已建成390 MW风力发电装机、310 MW光伏发电系统,本文将该能源基地的风力、光伏发电装机容量作为本文风光部分的规模,并选取该能源基地实地的天气数据(当地气象局)及周围用户负荷数据(国家统计局),为该风光系统配置合适的储氢容量。
风力发电和光伏发电的供电能力与风速和太阳能辐射强度息息相关。因此本文将分析该能源基地在2022年的风速和太阳能辐射强度情况,选择该年中日总太阳能辐射强度最大、最小,日平均风速最大、最小的四种极端情况进行分析,如表4所示。所选天气的风速和太阳辐射强度如图3所示。

Table 4. Four extreme weather conditions
表4. 四种极端天气情况
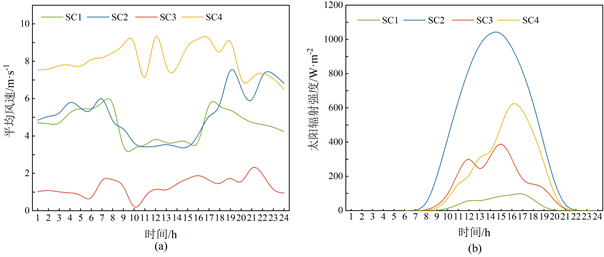
Figure 3. The wind velocity and solar radiation intensity of the selected weather
图3. 所选天气的风速与太阳能辐射强度情况
6. 结果与讨论
6.1. 四种极端情况对比
本文提出的风光氢储能系统在四种极端天气中的运行状态如图4所示。其中横坐标轴的上半部分表示在每个时间间隔内系统产生的能量,下半部分表示系统用于储存的能量。用户的负荷数据采用三段均值阶梯线段法处理。从图4可以看出,同时利用光伏和风电可以缓解它们的间歇性,但还是存在一些供应不足和大量能量浪费的情况。
四种天气均存在供应不足,需要燃料电池补充供应的情况。其中SC3风力最小时最为显著。如图4(c)所示,由于在该天气条件下,风速均小于风力发电机的额定风速,风力发电系统不运行。而光伏发电系统只在白天启动。因此,在这种天气情况的夜间时,风光发电系统就没有电力输出。另外,由于太阳能辐射强度的波动性,即使在白天,也会出现负荷缺失的情况,需要储能系统的补充供电来满足用电负荷。
从图4可以进一步观察到,在SC2太阳辐射最大和SC4风力最大的情况下,由于丰富的风光资源,系统产生的能量大大超过了负荷水平,不启动储能装置将产生大量的资源浪费。四种情况配备的最佳储能装置容量如表5所示。可以看出,四种情况下最大储能容量为:电解槽132.62 MW,燃料电池49.68 MW,储氢罐1100.75 km3,且均发生在SC2情况下。这是因为SC2太阳能最为充分,光伏发电量大,使电解槽容量最大。但同时SC2情况发生在夏季,用户的用电量大,导致燃料电池发电量也最高。因此,接下来将综合四种情况分析系统的储能配置。

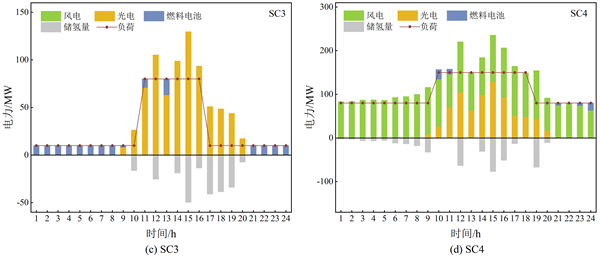
Figure 4. Daily running status of the system in four cases
图4. 四种情况下系统日运行状态

Table 5. The optimal configuration of hydrogen storage system in four cases
表5. 四种情况下储氢系统最佳配置
6.2. 综合四种极端情况分析
针对最佳燃料电池容量,综合SC1太阳辐射最小和SC3风力最小的情况,同时选取最大用户负荷数据进行优化分析,结果如图5(a)所示。在高需求和低产能的极端情况C1中,全天都需要燃料电池进行补充供应,最大电池容量为199.98 MW。针对最佳电解槽和储氢罐容量,综合SC2太阳辐射最大和SC4风力最大的情况,选取最小用户负荷数据进行优化分析,结果如图5(b)所示。在高产能和低需求的极端情况C2中,储能系统全天工作,最大电解槽容量为333.58 MW,对应的储氢罐容量为2768.71 km3。
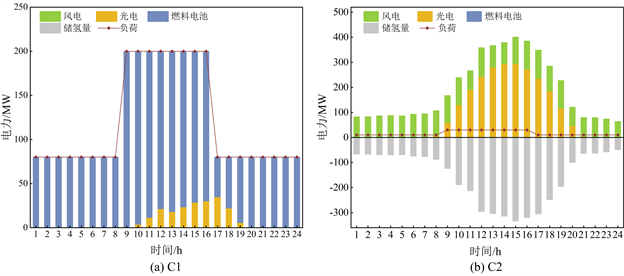
Figure 5. Comprehensive analysis of four cases
图5. 综合四种情况分析
6.3. 能源和经济分析
为了进一步确定储能容量,本节计算了SC1、SC2、SC3、SC4和C1 + C2五种情况的NPV,只有当能源系统的NPV在预测的10年内为正值时,经济分析才有意义。储能系统的设备价格如表6所示,计算所得的NPV见图6。可以看出,在预测的10年内,仅在C1 + C2情况下的系统NPV为负,因为其资本支出远大于储能发电收入。因此虽然C1 + C2情况能最大限度保证系统稳定运行,但其不具备经济性,本文不予考虑。
在综合经济和系统稳定性两方面,最终确定选用SC2情况下的储氢配置,即132.62 MW电解槽、49.68 MW燃料电池和1100.75 km3储氢罐。该配置下的系统能源增长率为24.72%,投资回收年限为4.6年,NPV为2.38亿元。

Figure 6. NPV of system in five cases
图6. 五种情况下系统净现值对比图
7. 结论
为缓解风能、光能的不稳定性和对系统负荷缺电、能量冗余等方面进行补偿和优化,本文提出一个风–光–氢互补发电系统优化模型,采用遗传算法,得到最优的储能装置容量。将所提出的模型应用于实际案例,选取日照辐射最强、最弱,日平均风速最大、最小这四种特殊天气情况对系统进行优化分析,得出以下结论:
1) 与常规发电系统相比,配备储能系统在四种天气情况下均有显著优势,最优配置方案可提高24.72%的能源增长率。该配置由390 MW风力发电机组、310 MW光伏发电机组、132.62 MW电解槽、49.68 MW燃料电池和1100.75 km3储氢罐组成。
2) 对系统进行经济性分析,在最优配置下,系统的投资回收年限为4.6年,NPV为2.38亿元,在保证经济性的同时提高了系统的能源利用率和供电可靠性,满足可持续发展理念。
3) 但本文在数据选择方面,只选取了典型的天气条件进行分析,没有基于全年数据求解最佳储氢容量,存在一定的不准确性,未来的工作中将基于更多的实际数据进行分析预测,减少系统不确定性。
基金项目
国家自然科学基金青年科学项目(62003215);国家自然科学基金面上项目(71974129)。
参考文献
符号说明
NOTES
*第一作者。
#通讯作者。