1. 引言
我国当下地区城市配网中大多为“闭环设计,开环运行”的供电模式 [1] [2] 。随着经济的快速发展,电力用户对电能质量也提出了新要求,为了提高电能的可靠性,降低用户端的电能损耗。通常电力调度人员对10 kV馈线进行合环操作,但是不同的合环方式下 [3] [4] ,合环馈线之间由于存在一定的电压差,相角差,合环时会产生较大的合环稳态电流,冲击电流,对电网设备产生较大的危害。
现有大量的研究成果对电网采用理论等值之后,分别从不同角度分析了合环电流怎么产生,以及相应的理论计算。文献 [5] 通过等值电路评估出不同合环方式下的相角差范围,但是对于实际电网众多参数没有考虑进来,比如110 kV母线的运行方式,以及110 kV母线其他馈线的负荷分布都对10 kV母线的相角有一定的影响。所以计算精度相对不太可观,文献 [6] 对馈线等值之后,讨论了三种计算方法进行合环计算。并分析了每种方法的实用性。文献 [7] 从时域的角度出发,一定程度上提高了合环电流计算的精度。文献 [3] 提出一种基于戴维南等值对合环电流计算的方法分别采用戴维,并将负荷考虑放在馈线的首末异端,但是没有考虑母线相角差的影响也没有考虑到不同馈线长度分布的影响。基于前者对合环冲击电流的估计算法,文献 [8] 提出了一种最佳频率法精确求取合环冲击电流。文献 [9] 中将绝对均匀的将负荷分布在馈线上,没有考虑到馈线可能出现某些地区的馈线负荷分布呈现前端较重末端较轻等情况,相对理想化该情况可能会产生更大的合环电流。不太切合实际情况,文献 [10] [11] 给出合环电流计算考虑了三相不平衡度的指标,但是只针对了低压用户进行了分析计算,由于要把理论研究应用到实际工程中,各地区都开展了一定的合环试验,文献 [12] 基于地区电网的现场试验建立等值模型,潮流计算,分析了合环转供电对电网的影响,主要进行的是先试验后分析。文献 [13] [14] [15] 分别从母线负荷电流的影响,最终提出了抑制合环电流的方法。文献 [16] 将负荷考虑为递增、递减、均匀分布三种模型,但是没有考虑建立更标准的上级电网模型,也没有考虑到负荷直接集中分布情况下的最大合环电流。并未考虑到三相不平衡问题,由于低压配电网中营销人员装表接电为了方便,总是在某一相易于操作的电源进行,存在大量的三相不平衡现象 [17] ,在此基础上如果不考虑三相不平衡度进行合环操作,很有可能会造成变压器桩头、设备线夹等经常烧坏。
为此,本文通过推导合环电流计算公式分析,首先利用DIgSILENT软件建立更符合实际的地区电网,有效地估计出合环馈线10 kV母线的相角差,得到相应馈线的相角差之后再导入简化的等值网络加入考虑负荷分布以及三相不平衡指标对合环电流进行分析,最后再与实际合环试验对比发现,所提方法计算误差符合实际工程要求,具有一定的实际意义。
2. 10 kV配电网合环类型
目前随着配电网的结构越来越复杂配电网合环类型也繁多,常见的合环方式主要分为两大类分别其一是相同站内的合环方式,其二跨地区的不同变电站之间的合环运行,同一站类根据电压等级不同又分三大类,(1) 10 kV母联开关与10 kV馈线形成的环网,(2) 110 kV母联开关与10 kV馈线,(3) 220 kV母联开关与10 kV馈线之间的环网运行,同样,不同变电站之间根据形成合环的电压等级也可分为以上几类。其中同一测变电站类的三种类型合环由于母线都来自同一变电站,合环母线的电压差较小甚至为零,合环过程也不会产生较大的循环功率,此类合环风险较小本文不讨论。本文主要讨论两组具有代表的合环模式,模式一为电压等级为220 kV同一地区的两个变电站与110 kV下的10 kV之间的电磁环网,其二为电压等级为500 kV下的跨地区的220 kV下10 kV馈线之间形成的电磁环网如图1所示。对应的模型参数如表1所示。
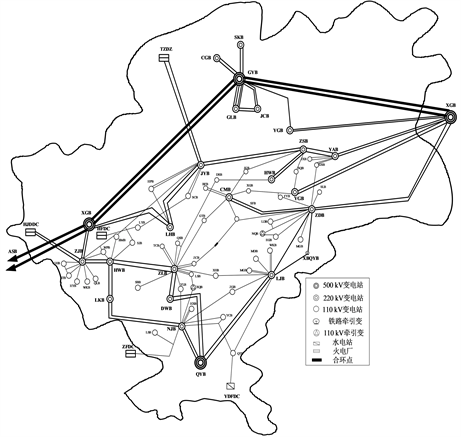
Figure 1. Partial geographic schematic of the regional power grid
图1. 地区电网部分地理示意图

Table 1. Measured parameters of the ring network experiment
表1. 合环试验实测参数
3. 合环理论分析
3.1. 合环潮流分析
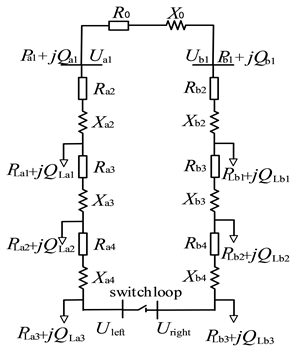
Figure 2. Equivalent network considering load distribution
图2. 考虑负荷分布的等值网络
如图2所示为实际电网考虑不同负荷分布的等值电路,由于合环之前
不相等,所以合环之后对整个网络亦会产生一定的循环功率,从而产生了循环电流,设循环功率
。
设Ulfet,Urigth分别是合环开关两侧电压,则有
(1)
电压又可写成如下:
(2)
联立上式(1) (2)可得
(3)
(4)
我们主要讨论电压差,以及相角差对循环功率的影响,对于配电网的10 kV侧一般电压相角差都相对较小,可假设:
,
,
。
所以对上式分别求偏导可得;
(5)
(6)
(7)
(8)
可以看出循环功率主要和网络的等值阻抗成反比,电压差对有功潮流的影响小于相角差对有功潮流的影响,电压差对无关潮流的影响较大。
3.2. 合环稳态电流分析
对于图中馈线注入功率,母线电压可通过实际电网运行的SCADA系统获取合,对于负荷功率无法准确获取,可以通过馈线母线参数进行估计。上级电网的等效阻抗根据公式(9)迭代求取 [16]
(9)
上式中通过按一定的步长增加l,最终使得下式中Ue趋于零是可有效的获得上级电网的等值阻抗。
(10)
(11)
对于母线处的电压幅值相角,通过DIgSILENT软件获取,则电压关系如下:
(12)
(13)
沿线电压降落:
(14)
(15)
最后得到合环开关侧的电压横纵分量如下:
(16)
(17)
亦可表示为:
(18)
同理可获得合环开关另一侧的电压。
(19)
最后电压差如下:
(20)
当合环开关闭合之后,以上网络可看作简单环型网络处理,可由叠加原理求取合环电流 [18] [19] [20] 。
(21)
式中RΣ,XΣ,分别表示如下:
(22)
(23)
合环馈线电流:
(24)
(25)
式中Ia0,Ib0分别表示合环前馈线初始电流。
3.3. 合环冲击电流计算
在对电网等值电路分析获得其合环电流,下面对其求解合环冲击电流;
冲击电流最大值:
(26)
冲击有效值:
(27)
其中
,
,f = 50 Hz。
式子令
。
则最大冲击电流:
(28)
(29)
4. 10 kV馈线负荷分布处理
4.1. 负荷分布的处理
本文由于的合环简化模型主要是以考虑负荷分布情况以及三相不平衡度,首先两馈线负荷分别设置在主干线长度的百分之三十处,百分之六十处,以及馈线的末端,再根据试验当时的负荷情况,将负荷处理为以下几种方案,(1) 馈线A负荷全部挂于首端百分之三十处,馈线B负荷全部挂于末端。(2) 馈线A负荷全部挂于末端,馈线B负荷全部挂于首端百分之三十处。(3) 馈线A,B负荷平均分布于三个负荷节点上。
4.2. 负荷不平衡度的处理
对于位置等效完的负荷,考虑的实际工况下三相不对称运行情况下,可能会产生较大的单相冲击电流,因此本文加入10 kV配电网合环的不平衡指标 [10] εs以考量合环之后运行的安全性,εs具体计算公式如下。
(30)
式中:Smax为三相最大功率,Smin为三相最小功率。
根据相关国标规定电网正常运行功率最大不平衡度为10%。
5. 合环影响因素分析及合环条件
由公式(5) (6)可知,合环电流的主要影响因素有网络的等着阻抗,馈线两端的电压差,馈线的负荷分布情况,以及母线的相角差,由公式(6) (7)可知合环电压差主要影响馈线的无功功率分布,相角差对馈线有功功率影响较大,且通过仿真也表明合环两侧相角差对馈线合环电流影响最大,因此准确的估计馈线的相角差尤为重要。对于合环条件本文主要考虑合环稳态电流满足馈线动热稳定要求 [21] 。合环尖峰电流不超越馈线开关继电保护整定值,合环三相相序必须一致,三相不平衡度满足相关国标要求。
6. 仿真与试验对比分析
6.1. DIgSILENT简化建模
针对目前合环馈线相角差难以获取的问题,本文主要采用PSD-BPA进行全网准确仿真获取,由于本次合环对比试验在2021年2月2日早上进行,故该表2合环馈线母线相角。
本文利用PSD-BPA以贵州某市夏小方式为背景进行合环馈线母线相角估计,同时再利用DIgSILENT建立详细模型进行相角再次计算,最后求取平均值获取,计算结果见表2 。
上级电网的详细模型网络复杂,潮流计算速度慢,通过上级电网获取较为准确的相角之后,得到馈线简化参表3,再用DIgSILENT软件建立合环等值仿真模型如图3。

Figure 3. Specific ring network simulation using DIgSILENT in a certain location
图3. 基于DlgSILENT的某地具体合环仿真图
6.2. 计算结果与试验对比分析
对于不同负荷分布计算结果如表4,由计算结果表明不同负荷分布导致合环电流差别较大,尤其负荷水平较高的馈线。本次合环试验两个地区馈线负荷分布大多呈平均分布模型,基于DIgSILENT建立的简化等值仿真模型,将负荷均匀分布在馈线上,对应合环电流有效值如图4。
实际合环中对于合环点没有安装测量装置,只有合环馈线首端存在测量装置,无法得到实测合环电流值,对比平均负荷模型下合环馈线电流情况,利用软件设置仿真总时长为0.25 s,设置在0.1 s时发生合环动作,在合环后大约半个周波将出现合环冲击电流峰值。得到合环馈线两端线首电流变化曲线如图5,图6。
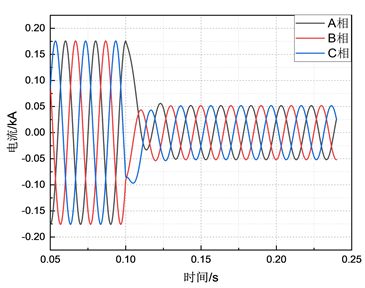
Figure 5. Current at the head of Dusixian line
图5. 都司线线首电流
由仿真结果图5合环之后馈线吉西线合环最大值约为50 A,有效值值35 A,现场合环实测为35 A,吉西线如图6,合环后最大值可达300 A,有效值212 A,现场实测240 A,结果表明通过建立的上级实际电网模型估计得到的相角较为准确。有力的反映了实际馈线的电流分布。馈线电流分布与实测结果对比见表5。考虑到实际负荷运行的不平衡情况,在三相不平衡运行下如果两条馈线上三相分布方向如果不一致,合环之后三相不平衡度可以得到均衡,但是如何三相不平衡度方向一致时可能会产生不平衡度越限情况,可能产生较大的单相冲击电流。

Table 2. Phase angles of ring feeder busbars
表2. 合环馈线母线相角

Table 3. 10 kV feeder line parameters
表3. 10 kV馈线参数

Table 4. Calculated results of closed-loop current for different load distributions
表4. 不同负荷分布合环电流计算结果

Table 5. Comparison of closed-loop current and actual error
表5. 合环电流与实际误差对比
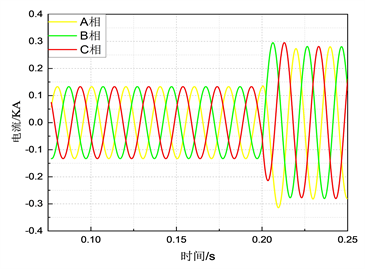
Figure 6. Current at the head of Jixi line
图6. 吉西线线首电流
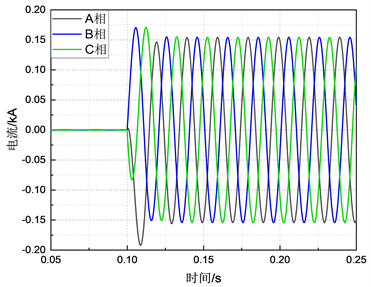
Figure 7. Three-phase balanced ring network impulse current
图7. 三相平衡合环冲击电流
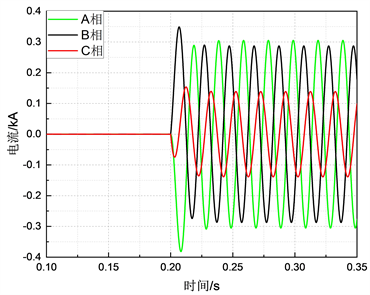
Figure 8. Three-phase unbalanced ring network impulse current
图8. 三相不平衡合环冲击电流
本文通过DIgSILENT软件仿真合环前三相平衡,三相不平衡方向一致情况得到合环电流分别如图7,如图8,图7可以看当三相平衡时合环之后的单相冲击电流大约为180 A,而图8为三相不平衡运行情况,合环之后的单相冲击电流可达到300 A。且三相不平衡度可达到40%,已超出相关标准规定,所以考虑该指标的边界条件,能有效的降低了不必要的合环风险。
7. 总结
本文综合考虑了10 kV合环馈线在三相不平衡和不同负荷分布情况下,针对两个不同地区的合环电流计算,借助潮流分析软件有效地估计出10 kV母线的相角差,利用估计的相角对地区合环电网进行等值计算,且模拟了现实情况下的负荷分布情况,分析了实际可能出现的边界合环电流,得到以下几个结论:
1) 在考虑不同负荷分布情况的计算中,合环电流的有效计算能够更准确地覆盖实际负荷不确定性,提高计算结果的实用性。
2) 考虑三相不平衡情况下,当三相不平衡方向不一致时,合环后不平衡度可能会缓解,但当三相不平衡方向一致时可能会导致更大的合环电流。
3) 计算结果与实际合环试验进行对比,表明模型计算的误差相对较小,验证了模型在实际工程中的实用性。使用DlgSILENT软件有效减少了合环电流计算的工作量。
综合而言,通过潮流分析软件和模拟负荷分布,该研究为合环电流计算提供了更精确的方法,并在实际工程应用中得到了验证。
参考文献