1. 引言
随着信息技术发展和经济的增长,企业间、地区间、国家间的信息交流和商品贸易更加频繁。随着交通网络的发展和交通工具的进步,供应链的范围和规模逐渐扩大,从上世纪七十年代得到了快速的发展。原料供应商,制造商,零售商、物流企业等之间的合作和联系逐渐加强,构成了复杂的供应链网络。但是,供应链网络也呈现出复杂且脆弱的特点。当供应链中的一个企业因为自然的和人为的因素无法正常运作时,产生的风险会沿着供应链网络向上游和下游的企业传播,比如上游企业的商品无法售出,占用库存和资金,下游企业无法获得所需的资源,因此无法进行生产制造活动。一些企业可能会承受不住风险而导致破产失效,风险进一步传播给其他企业,造成供应链网络一定规模的瘫痪。这就是供应链网络的级联失效现象。
级联失效会给供应链网络造成一定规模的瘫痪,严重的可能会导致整个网络的失效。级联失效现象广泛地存在于现实的供应链网络中,造成了巨大的经济损失,预防供应链中断,维持供应链稳定对经济发展和人民生活有着非常重要的作用。尽管可以采取一些人为的措施降低级联失效发生的概率,但是一些不稳定的因素,例如自然灾害、恶意竞争和人为经营不善等往往会造成网络中节点的失效,导致级联失效发生。
级联失效现象不仅存在于供应链网络中,在电网 [1] ,交通网络 [2] ,基础设施网络 [3] 等也时有发生。为了降低级联失效对供应链网络的影响,研究影响级联失效的因素,国内外学者在级联失效方面进行了大量的研究。Motter等 [4] 提出了负载–容量级联失效模型,并在无标度网络和真实网络上进行了实验。后来有大量的研究者基于此模型进行了级联失效方面的研究。Nie Tingyuan等人 [5] 使用映射熵来判断节点的重要性,并模拟该节点失效后导致的级联失效对网络的影响,证明该方法在识别重要节点的有效性。Yang Yue等人 [6] 提出一种非线性的负载–容量模型,网络中节点的容量和负载并不是线性关系,而是一种非线性关系。通过在BA网络上仿真实验,证明该模型比线性的负载–容量模型能够增加网络的鲁棒性。李淑敏 [7] 等人考虑到节点负载过低也会失效,研究了在不同初始节点失效时,低载引起的级联失效在生鲜网络中的传播情况。现实生活中,一些网络由双层网络组成,例如供应链网络和通讯网络,电网和基础设施网络。王建伟等人 [8] 考虑边权重及相互依赖网络间耦合强度的基础上,构建了相互依赖的双层网络级联失效模型,比较网络间不同耦合方式对网络鲁棒性的影响,并提出保护策略。
大部分的文献在研究级联失效问题时,认为节点的负载只与节点的度或介数呈线性或非线性关系。但是,在供应链网络中,即使是度比较小的节点也可能会因为是网络运输的枢纽而承担大量的仓储物流任务。在负载–容量模型中表现为节点在网络中的负载同时与节点的度中心性和介数中心性有关。所以,本研究在负载–容量模型的基础上,综合考虑节点的度和节点的介数来设置节点的负载,将负载分为生产负载和运输负载,并在BA无标度网络和ER随机网络上进行仿真模拟,研究在不同初始节点失效的情况下,网络鲁棒性的变化。
2. 理论概述
2.1. 图论基础
从哥德斯堡七桥问题提出以来,复杂网络被广泛地运用在现实网络的研究中,包括电网,交通网络,社交网络。供应链网络可以抽象为一个复杂网络
,其中节点集合
代表企业,边集合
代表企业之间存在联系,包括贸易关系、合作关系等。
2.2. 度中心性
度中心性是指网络中与节点存在连边的节点个数,即邻居节点个数,在供应链网络中,节点的邻居节点越多,表示与该节点企业有合作的企业越多,企业越重要。
2.3. 介数中心性
介数中心性是指在复杂网络中,通过一个节点的最短路径的数量占所有最短路径数量的比例。计算公式如下:
(1)
式(1)中,
是网络中的最短路径数量,
是通过节点i的最短路径数量。一个节的介数越大,表示通过该节点的最短路径数量越多,节点是一个交通枢纽的位置。在供应链网络中,节点的介数越大,说明该节点承担更多的货物运输、仓储、中转等功能。
2.4.网络模型
2.4.1. BA无标度网络
以往的研究证实了供应链网络存在无标度特征。本文选择BA无标度网络进行研究。BA无标度网络模型是Albert-LászlóBarabási等 [9] 在1999年提出的网络增长模型。BA网络在增长过程中,新加入网络的节点会优先选择网络中度比较大的节点,符合现实的情况,即新企业更愿意跟大企业进行合作,部分研究也证明了现实的供应链网络符合BA网络的特征,即度分布呈幂律分布。具体生成步骤如下:
Step 1:网络中存在m0个节点,节点之间相互连接。
Step 2:每一个时间步,一个新节点加入网络,并选择网络中的m (m < m0)个已经存在的节点建立连接。每个旧节点i被选择的概率为:
(2)
式(2)中,ki是节点的度,N是网络中已经存在的节点。
Step 3:重复Step 2,经过一定时间步t后,生成一个具有N = t + m0个节点的BA无标度网络
2.4.2. ER随机网络
除了BA网络外。部分现实中的网络符合随机网络的特征。ER随机网络是Paul Erdős和AlfrédRény在1959年 [10] 提出的网络模型,特征是网络中的节点间根据一定概率p随机建立连接:在给定节点数N的图中,遍历网络中的所有节点对,每次生成一个随机数,当随机数小于概率p时,节点间建立连接,否则不建立。最后生成节点数为N,连接概率p的随机网络。
3. 级联失效模型
本研究使用经典的负载–容量模型研究供应链网络上的级联失效问题。初始状态下,每个节点会有一定的负载和容量。当网络受到外在的扰动后,部分节点失效。失效节点的负载将会被分配给邻居节点。邻居节点增加额外的负载后,部分节点可能会超出自身的容量,导致失效,失效节点的负载再一次重新分配,直到没有节点超载或网络中所有的节点失效。
3.1. 节点的初始负载与容量
节点的负载是指网络中的节点需要处理的任务量,比如电网中电站的发电量,交通网络中交通枢纽需要借贷的客流量,供应链网络中企业的产品量和物流运输量。许多文献表明,节点的负载与节点的度有关。在供应链网络中,节点除了要承担上下游企业的制造任务需求,还可能作为网络枢纽和中转站,承担部分的物流、仓储等工作。因此本研究将节点的负载分为生产负载和运输负载,计算公式如下:
(3)
式(3)中,
是节点的初始负载,ki是节点的度,Bi是节点的介数,b是可调参数。
是节点的生产负载,α是节点度的归一化指数;
是节点的运输负载。式(2)表示,在供应链网络中,为了扩大企业的利润,作为节点的企业除了基础业务,即上下游企业的商品制造业务,还可以承接一定的物流运输任务,作为物流中转站发挥仓储,中转等作用。因此,企业的工作量受相邻企业数量和网络所处位置影响。所以本研究种节点的负载与节点的度和介数有关,且节点的运输负载是可调的,表示企业接受运输任务。
节点的容量是节点能够正常处理的最大的负载,在供应链网络中表现为节点企业能够承担的最大业务量。根据以往的相关研究,节点的容量和负载成正比,本研究设置如下:
(4)
3.2.负载重分配策略
在节点失效后,节点的负载将分配给邻居节点。已有的研究中,节点失效后会根据邻居节点的度、负载、容量、连边强度等分配负载。本研究采用根据节点容量分配负载的方法。公式如下:
(5)
(6)
式(5)中,Гi是失效节点的邻居节点集合,Cj是节点j的容量,πj是失效节点的容量占邻居节点总容量的比例。在节点i失效后,邻居节点j增加的负载为ΔLj。
3.3. 鲁棒性指标
鲁棒性是指网络在一些节点或者边失效导致网络发生级联失效后,网络能够保持自身结构和功能的能力水平。在级联失效后,为了衡量网络抵抗级联失效的能力,本研究采用级联失效后未失效节点比例P作为衡量指标,计算公式如(7)式:
(7)
式(7)中,
是级联失效后未失效节点数量,N是网络中节点总数量,N0是初始失效节点数量。级联失效结束后,P越大,表示级联失效导致失效的节点越少,网络的鲁棒性越强。
4. 仿真模拟
4.1. 相关参数设置
本研究在节点规模N = 200,平均度m = 3的BA网络和N = 200,连接概率p = 0.03的随机网络上进行级联失效的研究。为了研究运输负载大小对级联失效的影响,b分别取0,1。由于供应链网络比较容易遭受各种自然灾害、意外事故或交通管制政策导致节点失效,所以本研究采取随机攻击策略:网络中随机一部分的节点失效,导致级联失效发生。本研究初始失效节点数n = 20,为了保证结果的准确性,每次随机取不同的初始节点进行攻击,重复100次,最后结果取平均值。同时,还研究了失效节点数n对网络鲁棒性的影响。
4.2. BA网络仿真结果分析
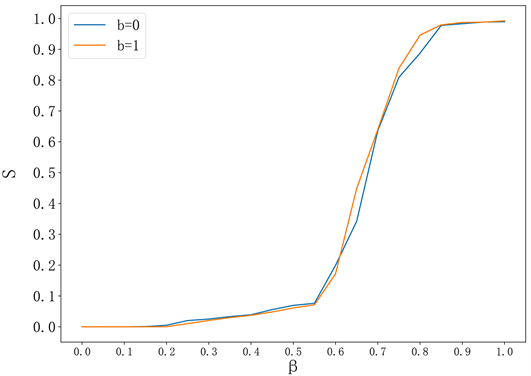
Figure 1. The impact of transport load factor b on the robustness S of BA network
图1. 运输负载系数b对BA网络鲁棒性S的影响
图1是运输负载对网络鲁棒性的影响结果,b分别取0和1,表示是否有运输负载。从图1可以得知,网络鲁棒性S随着β增加而增加。当节点的负载容量系数β小于0.6时,节点增加运输负载后,鲁棒性S比无运输负载时降低,表示有更多的节点失效。而当节点的负载容量系数大于0.6时,节点增加运输负载后,网络的鲁棒性S提高。这是因为,当节点的容量系数β较小时,节点比较容易因为负载增加导致过载失效。当b = 1时,节点的初始负载除了生产负载,增加了运输负载。初始节点失效后,分配给邻居节点更多的负载,即使邻居节点容量随着初始负载增加而增加,但是因为BA网络中节点负载的异质性较大,且β较小,提高的容量无法吸收多余的运输负载,此时失效节点的邻居节点比无运输负载时更容易失效,因此导致负载进一步分配给更多的节点导致失效,网络的鲁棒性S下降。而当β大于0.6后,节点增加的容量可以吸收失效节点多分配的运输负载,节点比b = 0时不容易失效,从而控制负载分配范围,抑制风险的传播,网络的鲁棒性S增加。
图2是当b = 1时,初始失效节点数n对鲁棒性S的影响变化。从图2可以明显看出初始失效节点数对网络鲁棒性S有明显的影响。当β一定时,不同失效节点数n对鲁棒性的影响较大。Β = 0.6时,n = 10的网络鲁棒性比n = 20时高了约0.6。这是因为无标度网络中,度和介数的异质性较高,因此网络对随机攻击的鲁棒性较好,对蓄意攻击的鲁棒性较差。当初始失效节点数n增加时,负载较高的节点失效的概率更大,所以n增加会导致网络的鲁棒性更快速地下降。同时,当初始失效节点数n = 40时,网络的鲁棒性也依旧大幅下降,说明当小节点失效达到一定数量时,也会造成网络较大的损失。
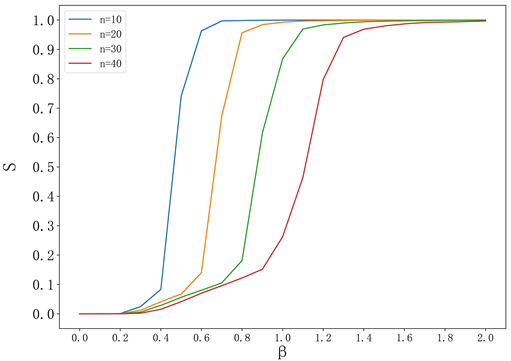
Figure 2. The impact of the number of failed nodes n on the robustness S of BA network
图2. 失效节点数n对BA网络鲁棒性S的影响
4.3. ER网络仿真结果分析
图3和图4是在ER网络上模拟的结果。从图3可以看出,当b = 1时,即初始负载包括生产负载和运输负载时,网络的鲁棒性S有少量的提升。相比于BA网络,b = 1时的ER网络鲁棒性S总是比b = 0时要高。这是因为ER网络的节点的异质性较小。节点初始负载增加,容量也会增加,能够更多吸收失效节点多余的负载而不会失效。图4是当b = 1时失效节点数对ER网络鲁棒性S的影响。初始失效节点数n对网络鲁棒性S的影响也是比较大的。相等初始失效节点数的情况下,和BA网络相比,ER网络的鲁棒性S > 0需要的最小容量β0较大,这是因为BA网络中节点负载的异质性较大,当部分节点失效后,邻居节点中容量较高的节点可以吸收更多失效节点的负载;ER网络中节点负载的异质性较小,当节点失效后,邻居节点能够吸收的负载比BA网络小,节点更容易失效。所以ER网络的β0比BA网络大。
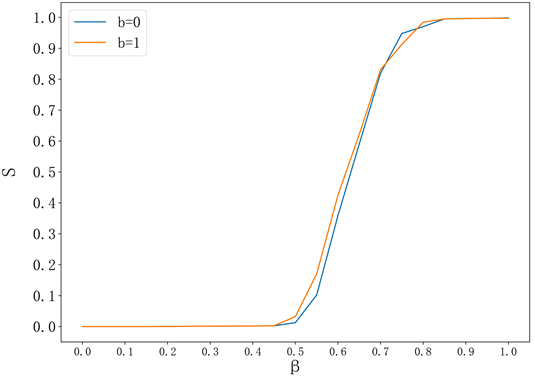
Figure 3. The impact of transport load factor b on the robustness S of ER network
图3. 运输负载系数b对ER网络鲁棒性S的影响
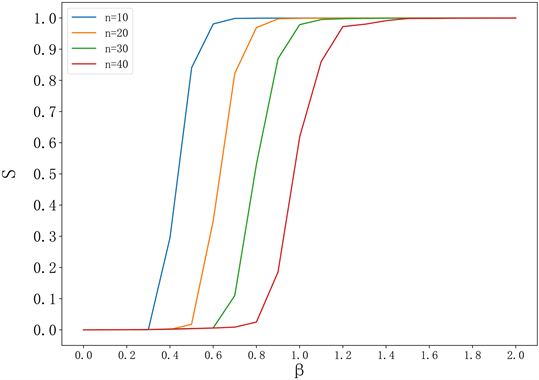
Figure 4. The impact of the number of failed nodes n on the robustness S of ER network
图4. 初始失效节点数n对ER网络鲁棒性S的影响
5. 结论
供应链网络中的企业除了生产制造任务外,还可以承接一定的物流运输订单。所以在级联失效的研究中,节点的负载不仅包括生产负载,还包括运输负载。本研究探讨了运输负载对网络鲁棒性的影响,并在BA网络和ER网络上进行了级联失效的仿真模拟研究。研究发现,与只考虑生产负载的模型相比,节点的初始负载增加运输负载后,BA网络的鲁棒性先下降后上升,而ER网络的鲁棒性有较小的提升。同时初始失效节点数对BA网络和ER网络的鲁棒性都有较大的影响。因此可以对现实的供应链网络提出建议:1) 具有无标度网络度分布特征的供应链网络,在发展初期应注重主要生产制造业务,提升企业效益,物流等任务交由第三方企业承担,以此来增加网络的鲁棒性;当企业的规模发展后,在应对风向的能力提高后,可以适当拓展新的业务,比如物流,仓储等业务,此时企业的效益增加,网络的鲁棒性也有一定的提升;2) 具有ER网络度分布特征的供应链网络,除了主要的生产制造业务外,也可以承接一定的物流仓储等业务,增加企业效益的同时也增强了整个供应链网络的鲁棒性。3) 在研究中,供应链网络中一些较小的节点失效后也可能会造成网络较大的损失。所以政府或相关企业应给予小企业适当的加强对供应链网络中小企业的保护,提高小企业应对风险的能力。减少小企业破产的概率,防止引发供应链网络的级联失效造成损失。