1. 引言
合作在社会中扮演着重要角色,从家庭到政治、从商业到文化,合作是社会运作的基石,社会中的每一个角落都充满了合作与背叛的复杂交织 [1] [2] 。社会中的每一个个体都面临着平衡个人利益与共同利益的挑战,这种挑战既能推动合作、共赢,也可能导致竞争、损失。因此,群体之间合作的出现与维持引起了广泛的关注和研究,许多领域的专家和学者对这个领域都很感兴趣,其中基于演化博弈论的研究更是吸引了大批专家学者 [3] [4] 。
从现有的研究成果来看,促进社会困境中合作行为有很多重要的机制,其中典型的有亲缘选择 [5] [6] 、直接互惠 [7] [8] [9] 、间接互惠 [10] [11] 、群体选择 [12] [13] 等。在过去的几年,个体的个人属性对合作的演化也受到了很多的关注,如声誉 [14] [15] 、迁移 [16] [17] 、记忆 [18] [19] 、惩罚 [20] 、期望 [21] [22] 等机制。其中关于节点的期望机制,Chen和Wang [23] ,采用随机学习更新规则,在小世界网络上研究了囚徒困境博弈中合作的演化规律,发现存在一个最优的期望收益可以使得更好的促进合作的演化。Zhang和Liu等人 [24] 将一种基于期望的重连机制引入空间公共物品博弈中,研究发现中等的期望水平最能促进合作,并且发现中等的期望水平会导致节点度的异质分布,也有利于合作的演化。Zhang和Huang等人 [25] ,将基于期望的策略坚持引入囚徒困境博弈中,节点可以根据期望收益调整自己策略的坚持时间,通过研究发现,基于期望的策略坚持可以有效的促进系统中的合作水平。
基于上述内容,在本文中,我们提出了一种新的博弈规则,将基于期望的休眠机制引入囚徒困境博弈中。节点会根据自己本轮的期望收益是否满足期望收益,然后以一定的概率去选择是否参与下一轮的博弈,通过仿真表明,该机制可以显著的促进合作的演化。
本文的其余部分安排如下,第二节介绍详细了基于期望的概率休眠机制的模型,第三节通过仿真对结果进行了分析和讨论,最后对全文进行了总结。
2. 演化模型
囚徒困境常常用来研究群体中合作和背叛策略的选择。在本文中,我们假设群体中所有节点在L × L (L = 100)的具有周期性边界条件的方格网络上进行囚徒困境博弈,每一节点占据一个网格,并且每个节点拥有上下左右四个邻居,初始每个节点随机分配合作策略SC = (1,0)T与背叛策略SD = (0,1)T。如果两个博弈的节点都是合作策略,那么他们都将获得收益R,或者互相都选择背叛策略而收到惩罚P。如果两个节点中一个选择合作策略,一个选择背叛策略,那么合作者会受到傻瓜收益S,背叛者收到背叛诱惑T。因此,节点的收益矩阵可以表示为(1)式:
(1)
令
表示节点受到的背叛诱惑。在每一轮的博弈中,系统中所有节点依次与自己的四个邻居进行博弈,记节点i收到的收益为Pi,计算如(2)式:
(2)
其中Ωi表示节点i的邻居集合。
节点是否参与下一轮的博弈要依据自己本轮获得的收益与期望收益的关系,节点的期望收益Ei可以表示为(3)式:
(3)
称为期望收益参数,通过α来调整节点获得的期望收益,其中K表示的是节点i的邻居个数,固定为4。
在节点i获得本轮收益之后,节点会把本轮的收益与自己的期望收益相比较,并且以Qi的概率参与下一轮的博弈,以1 − Qi的概率选择休眠。节点i参与下一轮博弈的概率计算如(4)式:
(4)
其中β称为参与博弈参数。
如果节点i不参与下一次博弈,那么该节点会进入休眠,我们记录节点i已经休眠的时间为Ti(t),设定节点结束休眠的时间步为Td,初始每个节点的休眠时间都为0,节点的休眠时间计算如(5)式:
(5)
最后,节点同步更新他们的策略,中心节点i随机选择一个邻居j,节点i在下一轮博弈中学习邻居j的概率W计算如(6)式:
(6)
其中k表示非理性因素,在本文中固定k = 0.1。
3. 仿真与分析
我们将系统中的合作水平定义为
,它是系统达到稳定状态之后,系统中采取合作策略节点个数占总节点数的比例。本次实验通过5 × 105步蒙塔卡洛迭代,在每一轮演化迭代之后,取最后的5000步数据做平均,并且为了提高数据的准确性,结果所呈现的值是对实验做了50次仿真之后的平均值。
首先我们研究了节点的期望收益参数α与节点受到背叛诱惑b共同作用下,系统到达稳定状态时合作率,如图1所示。在没有引入期望收益机制时,即α = 0的时候,从图中可以看到,随着背叛诱惑b的增加,系统的合作率迅速便降为0。通过引入期望收益机制,随着α的增加,系统的合作率开始增加,并且可以看到系统中的合作者可以在一个期望收益α的范围内生存。固定背叛诱惑b,如b = 1.3时,在α = 0.01很小的时候,系统合作率为0,此时节点的期望收益很低,即使自己邻居中的背叛者节点占比较多的时候,节点也可以得到满足,所以更容易受到背叛者的入侵,最终导致系统被背叛者主导。随着α的增加,中心节点的期望收益变高,对邻居节点的策略要求也变高,系统合作率开始增加,在α = 0.3时,系统节点达到全合作状态。但是随着α的进一步增大,合作率迅速降为0。并且从图中可以看到,在α = 0.3的时候,系统中合作者可以在背叛诱惑b < 1.4的时候始终保持全合作,并且还存在一个α = 0.2,使得合作者在背叛诱惑b很大的时候也可以保持一定的合作率。以上结果表明,期望收益可以有效的促进系统中合作的演化,并且存在一个最优的α值使得系统中合作率最高。
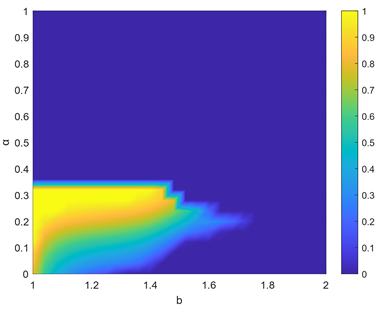
Figure 1. Evolutionary results of the cooperation rate under the combined effect of expected payoff α and betrayal temptation b, where β = 4, Td = 10, and k = 0.1
图1. 合作率在期望收益α和背叛诱惑b共同作用下的演化结果,其中β = 4,Td= 10,k = 0.1
节点在获得博弈收益之后会跟自己的期望收益做比较,然后以概率Qi参与下一轮的博弈,通过调节参与博弈参数β可以控制节点对期望收益的重视程度,系统节点随着β的演化情况,如图2所示。从(a)图中可以看出来,在β = 2比较小的时候,不论背叛诱惑b为何值,在到达稳定时,系统中的合作者都无法生存。增大β值,系统中开始出现合作者,并且在b < 1.4的时候可以始终保持全合作,然后随着背叛诱惑的b的增加系统中合作率逐步降低。当β = 6的时候,相对于β = 4时,系统达到全合作的阈值所对应的b值减小了,系统只能在b < 1.25的时候保持全合作。
在节点与自己的邻居进行博弈后,节点如果不满足自己的收益便会有很大的概率进行休眠,所以在系统达到稳定状态时会有一部分节点是不参与博弈的。如图2(b)所示,在β较小的时候,如β = 2,不论b为何值,节点都会选择休眠,系统稳定状态时参与博弈的节点比例只有0.1,最终导致系统的合作率为0。当β = 4时,随着背叛诱惑b的增加,在b < 1.4的时候,系统中节点的参与博弈率始终维持在0.99以上,继续增大b,由于背叛诱惑的增加,系统中合作者更容易受到背叛者入侵,为了保护自己的不被入侵,开始有更多的节点进入休眠,从图中可以看到,当b > 1.4的时候,系统中节点参与博弈率开始迅速降低。继续增大β,发现使节点保持较高参与博弈的b范围减小。

Figure 2. (a) Denotes the evolution result of the cooperation rate Fc; (b) denotes the evolution result of the participation game rate Gc; and (c) denotes the evolution result of the node’s average payoff Poff; where α = 0.3, Td = 10, k = 0.1
图2. (a)图表示合作率Fc的演化结果;(b)图表示参与博弈率Gc的演化结果;(c)图表示节点平均收益Poff的演化结果;其中α = 0.3,Td = 10,k = 0.1
由于部分节点休眠不参与博弈,那么他将无法获得与邻居博弈的收益,那些处在休眠阶段的节点的收益为0,这会导致系统中节点的平均收益也会收到影响。结果如图2(c)所示,在β = 2时,因为不论b为何值合作者都无法生存,所以系统中的平均收益为0。在β = 4,b < 1.4时,系统中的平均收益维持在一个较高的水平,随着背叛诱惑继续增大,节点的平均收益迅速降为0,此时系统节点为全部背叛状态。继续增大β,系统高平均收益的b范围缩小,此时系统中还存在的少量的合作者,所以系统的平均收益只能保持在一个很低的水平。

Figure 3. Evolution results of the cooperation rate under the joint action of the betrayal temptation b and the participation game parameter β, where α = 0.3, Td = 10, k = 0.1
图3. 合作率在背叛诱惑b和参与博弈参数β共同作用下的演化结果,其中α = 0.3, Td = 10, k = 0.1
为了探究背叛诱惑b与β共同作用下对合作率Fc的影响,我们绘制了图3。在β < 2.8的时候,可以看到,不管b取值多少,到达稳定状态后,系统都被背叛者主导。在b < 1.25的时候,随着β的增大,在β < 2.8时,系统都被背叛者所主导,继续β进一步增大,系统中开始出现合作者,并且保持很高的合作率,系统始终被合作者所主导。但是当
时,可以看到随着β的增大,系统先是被背叛者所主导,然后当β增大到一定值之后,开始出现合作者,在β达到3.8的时候,系统中的合作率达到最优值。继续增大β的值,系统会的合作率开始降低。在b > 1.5并且β值比较大的时候,因为休眠机制的存在,节点因为自己的收益不满足期望收益,所以更多的节点选择休眠,因此系统依然可以保持一定的合作率。以上结果表明,在b值取一定的范围时,存在一个最优的β值可以使得系统中的合作率最高,在参与博弈参数β和背叛诱惑b很大时,因为休眠机制的存在,系统可以保持较低的合作率。
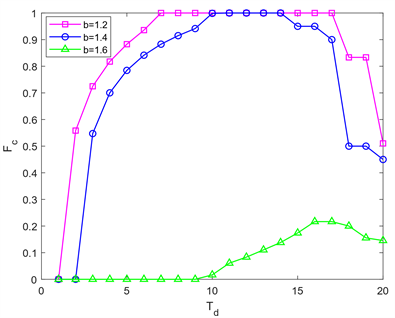
Figure 4. Evolution of cooperation rate with dormancy duration Td, where β = 4, α = 0.3, and k = 0.1
图4. 合作率随着休眠时长Td的演化结果,其中β = 4,α = 0.3,k = 0.1
为了进一步研究合作率与节点休眠时间的关系,我们绘制了合作率Fc关于休眠时间Td的演化结果,如图4所示。在b = 1.2的时候,随着休眠时长的增加,系统达到稳定状态时的合作率逐渐上升,在休眠时间达到6时,系统达到全合作状态,并且随着Td的继续增大,合作者始终占据整个系统,但是当休眠时间超过18时,合作率开始逐渐降低。在b = 1.4时,节点受到的背叛诱惑增大,系统达到全合作的最佳休眠时间的范围缩小。背叛诱惑继续增大到1.6时,系统在Td > 9时才会有合作者出现,但由于节点受到的背叛诱惑太大,合作率最高只能达到0.2左右。从实验结果可以得出,对于不同的背叛诱惑b,存在最优的休眠时间可以使得系统中的合作率最优。
最后为了观察系统的演化过程,我们绘制了系统节点策略的分布快照,如图5和图6所示,分别为固定背叛诱惑b为
,参与博弈参数β为
。从图5来看,在演化最初阶段,节点的策略随机分布在网络中,随着时间的演化,合作者开始形成合作者集群。在b = 1.2时,节点受到的背叛诱惑很小,合作者集群开始迅速扩张,并且很快便占据整个系统。在b = 1.6时,虽然最开始合作者也可以通过形成合作者集群来生存,但是由于背叛诱惑太大,合作集群很容易受到背叛者的入侵,最终导致背叛者占据整个系统。图6中,在参与博弈参数β = 2比较小时,系统中的合作者集群无法维持生存,随着时间迅速消失。在β = 6时,在系统到达稳定状态时,合作率可以维持较低的水平。从图5和图6可知,中等大小的参与博弈参数β更利于合作者的生存,这与前面的研究结果一致。

Figure 5. Evolutionary results of node strategy snapshots over time (Yellow for collaborators, blue for betrayers), (a~e): b = 1.2; (f~j): b = 1.4; (k~o): b = 1.6. where β = 4, α = 0.3, Td = 10, k = 0.1
图5. 节点策略快照随着时间的演化结果(黄色代表合作者,蓝色代表背叛者),(a~e):b = 1.2;(f~j):b = 1.4;(k~o):b = 1.6。其中β = 4,α = 0.3,Td = 10,k = 0.1
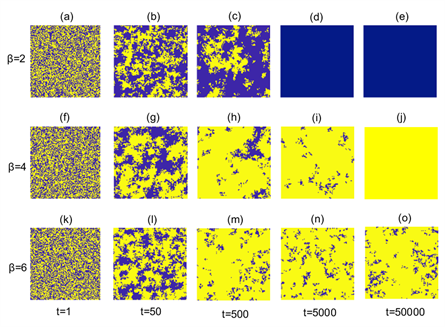
Figure 6. Evolutionary results of node strategy snapshots over time (Yellow for collaborators, blue for betrayers), (a~e): β = 2; (f~j): β = 4; (k~o): β = 6. where b = 1.4, α = 0.3, Td = 10, k = 0.1
图6. 节点策略快照随着时间的演化结果(黄色代表合作者,蓝色代表背叛者),(a~e):β = 2;(f~j):β = 4;(k~o):β = 6。其中b = 1.4,α = 0.3,Td = 10,k = 0.1
4. 结论
本文提出了一种基于期望的概率休眠机制,如果节点在与邻居博弈之后获得的收益不满足自己的期望收益,那么节点将会以一定的概率选择休眠,不参与下一轮的博弈,直到休眠时间达到Td时间步。我们首先研究了期望收益对合作演化的影响,发现存在一个期望收益范围可以使得合作者生存,并且存在一个最优的α值可以使得合作率最高。接着固定节点的期望收益,研究参与博弈参数β对系统合作率演化的影响,结果表明,中等大小的参与博弈参数β可以更好的促进合作者的演化,在背叛诱惑很大时,较大的β值可以使得系统仍然有少量的合作者存在。最后,我们研究了节点的休眠时间对合作演化的影响,发现对于不同的背叛诱惑,存在最优的休眠时间范围可以使得系统中的合作率达到最高。综上所述,基于期望的休眠机制可以显著的促进合作的演化。
基金项目
国家自然科学基金青年基金资助项目(61803264);上海市人工智能资助项目(2019RGZN01077)。
NOTES
*通讯作者。