1. 引言
相比于传统微创手术,机器人微创手术不仅继承了其创口小,感染率低等优点,还克服了医生视野狭窄,手眼不协调等诸多问题 [1] 。力反馈主手作为微创手术机器人系统的重要组成部分,是医生与机器人交互的接口,其灵活性,工作空间,反向驱动等性能直接影响医生的操作体验,进而影响手术的质量。为提高力反馈主手的综合性能,需要在确定主手的构型之后对其结构进行优化。为评价机器人性能的优劣,需要将机器人的性能与量化的指标相联系。常见的指标由可操作度指标 [2] ,条件数指标 [3] ,波动性指标 [4] ,动力学性能指标以及刚度指标 [5] 等。为更好的体现机械臂的综合性能,本文使用多个指标进行优化。
冗余关节在保证末端运动规律的同时,可以利用自身零空间的自运动产生不同的位形,广泛应用于各种协作任务中 [6] [7] 。这就涉及到冗余关节角选取的问题,需要对冗余关节进行规划。冗余关节的规划一般用于让机械臂拥有更好的灵活性 [8] ,避免机械臂到达关节限位 [9] ,回避机械臂奇异位置 [10] ,规避路径中的障碍物 [11] [12] 以及获得更优的动力学性能 [13] 等。本文采用加权最小范数法 [14] 规划冗余关节,避免机械臂达到关节限位。并用解析法求取其余关节角,进一步提高了逆运动学求解的精度。
2. 主手运动学建模
2.1. 正运动学分析
力反馈主手设计为串联机械臂,该机械臂有7 + 1个自由度,分别为7个旋转自由度和1个夹持自由度,如图1所示,在进行运动学分析时,夹持部分作为独立的机构,不影响手臂的最终位姿。采用改进的D-H法建立主手的各连杆坐标系,如图2所示,连杆D-H参数见表1。
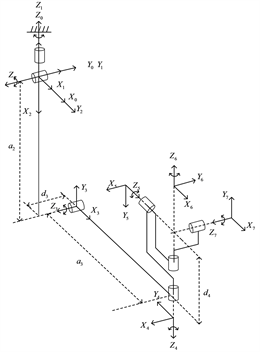
Figure 2. Master hand D-H coordinate system
图2. 主手D-H坐标系

Table 1. Master hand D-H parameter table
表1. 主手D-H参数表
根据D-H参数计算力反馈主手的正运动学,力反馈主手末端相对于基坐标系的齐次变换矩阵为
(1)
其中:
(2)
(3)
(4)
式中:θi为各个关节角,α和d为转角和偏距,
。
2.2. 逆运动学分析
由于该力反馈主手的连杆坐标系
的三轴交于一点,其构型满足peiper准则 [15] ,故存在解析解。
(5)
其中:
(6)
(7)
(1) 求解θ3
将式(2~4)等式两端平方和后相加得:
(8)
(9)
使用三角代换:
(10)
将式(10)代入式(8):
(11)
(12)
(13)
其中:
(14)
(2) 求解θ2
(15)
同理:
(16)
(3) 求解θ1
(17)
同理:
(18)
(4) 求解θ4
关节4作为一个冗余主动关节,用以提高主手腕部的灵活性,在下文中使用加权最小范数法求得,因此将该角度视为已知角度。
(5) 求解θ5,θ6和θ7
(19)
(20)
(21)
(22)
3. 主手多目标优化
在对力反馈主手的机构优化中,需要对手臂机构的杆长进行优化设计,以使得医生操作力反馈主手在其期望工作空间内达到最好的操控效果。定义相关的杆长参数
为设计变量。
3.1. 各性能指标分析
3.1.1. 运动学性能指标
运动学性能指标可以有效地反应机构的灵活性,灵活性在一定程度上反应机构的优劣,运动学性能指标包括速度最小值指标,各向同性指标以及可操作性。其中,可操作性是机构在可以产生运动的方向上对力的反映和等效为运动的能力,适用于主手的优化,可以有效表现机构是否存在奇异。可操作度指标被定义为
(23)
其中θ为关节角,J(θ)为对应的雅克比矩阵,但是,ω只能表现力反馈主手处于特定位姿时的运动能力,为了使其用于全局优化,将可操作性指标在其工作空间内取均值,并进行归一化处理。改进后适用于全局的可操作性指标定义为:
(24)
3.1.2. 刚度性能指标
机构的刚度使之在受到外界约束时抵抗弹性变形的能力,为避免力反馈主手由于自身刚度问题导致机构末端误差,将刚度性能指标作为主手优化指标之一。在基坐标下串联机器人第i部分在末端执行器所产生的柔度矩阵被定义为:
(25)
机构的整体柔度是将前置所有连杆的柔度累加,即:
(26)
机构的整体刚度矩阵定义为:
(27)
其中,B表示基坐标系,
分别表示平移矩阵、旋转矩阵、平移旋转矩阵、旋转平移矩阵。其中:
(28)
改进的全局刚度性能指标归一化处理后如式(29)所示,在此基础上构成的综合刚度性能指标如式(30)所示:
(29)
(30)
3.1.3. 动力学性能指标
机构动力学性能指标可以反映电机施加在机构上的力与机构在该力作用下运动之间的关系,为使力反馈主手在动力学方面表现出优良的性能,需要将刚度性能指标作为主手优化指标之一。采用拉格朗日动力学对主手进行动力学建模,即:
(31)
其中M(q)式惯性矩阵,
是科氏和向心力力矩,τ是驱动力矩。由于医生在操作力反馈主手时末端速度和加速度较小,因此可以将式中科氏和向心力力矩部分忽略,将上式简化为:
(32)
为了使其用于全局优化,将机构动力学性能指标在其工作空间内取均值,并进行归一化处理。改进后适用于全局的机构动力学性能指标定义为:
(33)
3.2. 优化模型建立
3.2.1. 优化目标
由上面所述的指标,模型的优化目标函数为:
(34)
3.2.2. 约束条件
如果力反馈主手的杆长过短,会使主手工作空间变小,需要更加频繁地进行离合操作,增加医生的操作难度,同时也会导致电机,驱动器等元件难以安装;如果力反馈主手的杆长过长,会导致整体机构体积过大,使得主手之间产生干涉,同时,过大的体积会增加主手连杆的重量,进而增大关节电机的负担。应尽量控制杆长符合人体工程学,提高医生的手术体验,综合考虑杆长约束条件为:
(35)
因此该优化问题中三个变量
的取值范围如表2所示:

Table 2. System resulting data of standard experiment
表2. 标准试验系统结果数据
3.3. 优化算法选择
在多目标函数优化问题中所有目标函数无法同时达到最优,需要根据特定的条件进行取舍因此,多目标优化问题的解是一组帕累托最优解,因此需要在多样化的解选择一组满意解。为使目标函数在可行范围内取得一组满意解常用以下方法:第一种是求出大量非劣解并将其构成一个子集,依照决策者的意图选取,但该方法主观性较强且依赖决策者的经验,具有较大的局限性;第二种方法为使用优化算法,常见的多目标优化算法有粒子群算法,神经网络算法,模拟退火算法,遗传算法等。其中遗传算法借鉴了自然界中生物优胜劣汰的遗传机制,通过计算机模拟,能够搜索出逼近最优解的一组优化解。遗传算法借助概率化的寻优方式,能够随机,高度并行和自适应的调整搜索方向,不需要定义特定的搜索规则,具有较强的鲁棒性。且一般的迭代方法容易陷入局部最小陷阱,使迭代无法进行,遗传算法很好的克服了这一缺点,是一种全局的优化算法,适合求解复杂的非线性优化和多目标优化问题。因此,本文选择 NSGA-II遗传算法求解力反馈主手杆长的多目标优化问题,其中种群数量为50,进化代数设定为100代。
优化结果分析
应用散布矩阵能更加直观的表现出多目标优化问题中优化函数与力反馈主手杆长参数之间的变化趋势和相关性,如图3所示,矩阵图上三角显示为杆长参数与优化函数的相关系数,其值位于[-1,1]之间,相关系数越接近0,则二者越无关。由矩阵图可以得到:
1. f1与f2,f3之间的相关系数为−0.10,0.05,三个目标函数之间相关性并不大,因此三个目标函数可以独立地表示力反馈主手的不同性能。
2. a2与f1,f2,f3之间的相关系数为0.24,−0.42,−0.15,说明a2与f2,f3负相关,与f1正相关。
3. a3与f1,f2,f3之间的相关系数为0.11,0.44,0.29,说明a2与f1,f2,f3正相关。
4. d4与f1,f2,f3之间的相关系数为−0.16,0.24,0.52,说明a2与f2,f3正相关,与f1负相关。
所有优化函数均进行过归一化处理,所以三个优化函数的单位一致,力反馈主手部分参数值如表3所示,根据综合性能指标选取最优的力反馈主手杆长参数,综合性能指标表示为:
(36)
经圆整后主手杆长为:
(37)

Table 3. Partial optimization result
表3. 部分优化结果
4. 冗余关节规划
在三维空间中,一般的机械臂只需要6个自由度便可以达到工作空间中的任意位姿,但这样的机械臂存在关节限位,可达工作空间局限性高的问题。而拥有冗余自由度的机器人可以在保证末端运动不发生变化的同时,利用零空间的自运动产生不同的关节位形。通过上述方法已经得到力反馈主手的杆长参数,为避免关节角在运动过程中距离关节限位较近,对力反馈主手冗余关节进行规划。
4.1. 加权最小范数法
机械臂的雅可比矩阵将关节速度与笛卡尔速度联系起来。一个拥有n个自由度的机械(其中n > 6),其关节变量可由
表示,末端执行器的位姿由笛卡尔空间的坐标向量表示,对于关节型机械臂的运行方程表示为:
(38)
定义末端广义速度:
(39)
其中
是机械臂末端线速度,
是机械臂末端角速度(
用来表示机械臂末端得姿态,采用固定坐标系方法表示)操作臂末端位姿表示为:
(40)
广义速度与末端位姿之间的关系为:
(41)
关节速度的加权范数定义为:
(42)
其中W为正定对称矩阵,将正定对称矩阵,加权关节速度和加权雅可比矩阵定义为:
(43)
(44)
其中wi满足:
(45)
式中:
(46)
其中U(θ)为避免力反馈主手达到关节限位的优化函数,其定义为:
(47)
在基于优化函数的加权矩阵作用下,可以保证在求取力反馈主手逆运动学是避免关节限位对公式(47)求导得:
(48)
从式(46)可以看出:当关节角度向关节极限位置运动时,式(46)的值为正值,当关节角度向远离关节极限位置运动时,式(46)的值为负值。
将式(38)改写成加权关节速度与加权雅可比矩阵形式:
(49)
由式(49)得:
(50)
结合式(42, 50)得:
(51)
根据上一时间关节角度和关节速度求出该时间的关节角度:
(52)
综上所述,由式(51)和式(52)可求得主手的角度流程如图4。
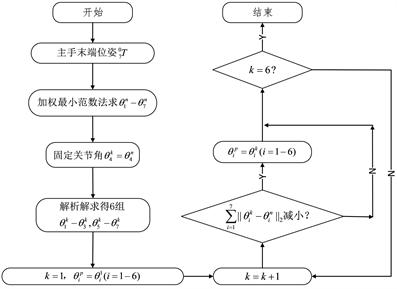
Figure 4. Redundant joint planning flowchart
图4. 冗余关节规划流程图
4.2. 仿真验证
将力反馈主手的初始位姿定义为:
(53)
其对应的关节角度为:
(54)
设定目标末端关节角度为:
(55)
设定时间为10 s,为保证机器人末端在10 s内从初始位置到目标位置采用匀速直线运动,广义速度表示为:
(56)
表4为关节角的限位:

Table 4. System resulting data of standard experiment
表4. 标准试验系统结果数据
图5为力反馈主手运动过程中各个角度变化,由图5可以看出所有角度均未接近关节限位。
为验证计算的准确性,将所求关节角代入式(1)解出在该组关节角下的位姿,同时通过式(57~59)将姿态转化为X-Y-Z固定角:
(57)
(58)
(59)
同时定义相对误差:
(60)
式中pu为求得的关节角度对应的末端位置,ps为实际的末端位置,结果如图6所示:
由图6可以看出误差最大的为Y角的相对误差,但误差依然未高于0.01%,因此可以保证计算的准确性。
为了较为清晰地判断仅用加权最小范数法求得的关节角度,和改进后使用解析法求得的关节角度之间的精度,定义跟踪误差:
(61)
式中pdx为使用两种方法求得的关节角度对应的末端位置,px为实际的末端位置,结果如图7所示。
5. 结束语
本文在建立力反馈主手的运动学模型后,将运动学性能指标,刚度性能指标和动力学性能指标设计为力反馈主手杆长参数优化的目标函数,并应用遗传算法求解该多目标优化问题,得到优化结果:
,为后续样机的研制奠定了基础。在已完成的优化变量的基础上,应用加权最小范数法以避免力反馈主手达到关节限位的优化函数为目标求得最优的冗余关节角度,然后用解析法求得其余关节的角度。仿真结果表明:该算法不仅能获得较为精确的逆解,并且可以很好的利用冗余关节的自运动,避免各关节在运动时接近关节限位,具有很高的实用性。
基金项目
国家自然科学基金资助项目(61803341)和浙江省自然科学基金资助项目(LY20E050019)。