基于一种新策略的级联失效鲁棒性研究

Study on Cascading Failure Robustness Based on a New Strategy

摘要: 考虑到级联失效时保留相似度最高的邻居节点，有助于减少失效节点对网络性能的负面影响，从而提高鲁棒性，提出了一种在级联失效过程中，保留与失效节点相似度最大的邻居节点的新策略。在新策略的基础上，对BA无标度网络、ER随机网络和WS小世界网络进行模拟仿真，并且对比新策略与原始策略的鲁棒性情况，仿真实验结果表明，网络的鲁棒性随着容量参数β的增大而增大；新的策略可以有效提高网络的鲁棒性，并且在BA无标度网络上的效果更明显，验证了该策略的可行性。

Abstract: Considering that retaining the neighbor node with the highest similarity can help reduce the nega-tive impact of the failed node on network performance and improve robustness, a new strategy is proposed to retain the neighbor node with the greatest similarity to the failed node during the cas-cading failure process. On the basis of the new strategy, the BA scale-free network, ER random net-work and WS small-world network are simulated, and the robustness of the new strategy and the original strategy are compared. The simulation results show that the robustness of the network in-creases with the increase of the capacity parameter β. The new strategy can effectively improve the robustness of the network, and the effect is more obvious on the BA scale-free network, which veri-fies the feasibility of the strategy.

1. 引言

复杂网络的发展经历了四个阶段：随机图论、小世界实验、小世界网络和无标度网络。Watts和Strogatz引入了小世界网络模型来描述将网络带到完全随机网络形成的完整规则集。Barabási和Albert使用幂律来计算许多实际复杂网络的连接度分布 [1] [2] 。这两个想法奠定了复杂网络的基础。近年来，复杂网络理论迅速发展，并已广泛应用于研究基础设施网络的鲁棒性，包括交通网络 [3] [4] 、物流网络、供应链网络 [5] 以及电网等 [6] [7] 。这些基础设施网络往往容易受到级联故障的影响，级联故障的特点在于部分节点出现故障时，会引发负载重新分配，可能使得某些节点负载超出其承载能力，从而导致故障规模扩大，最终威胁整个网络的稳定性。级联故障对基础设施网络的运行是致命的，这些基础设施网络在人类的生活中发挥着重要的作用，一旦被破坏，将严重影响人们的生产生活，造成巨大的人力、物力的损失。

为了提高复杂网络对级联故障的鲁棒性，学者们从节点初始负载、容量分配策略、负载再分配策略等不同角度进行了研究。Motter等 [8] 提出了一种经典的ML负载模型，该模型认为网络信息在节点之间沿最短路径交换，因此将节点的间性定义为节点的初始负载。同时，由于成本限制，他们假设节点的容量与其初始负载成正比，这种容量分配策略被许多研究采用 [9] [10] [11] [12] 。Wang等 [13] 将节点的初始载荷定义为节点的度与相邻节点的度和的乘积，与节点间中心性呈正相关 [14] 。Liu等 [15] 提出一种基于多变负载的负载分配策略，通过将节点剩余容量充分利用从而减少网络级联失效。唐亮等 [16] 构建一种故障概率传播的级联失效模型，节点故障概率随故障次数的增加而减少，网络失效规模减少。Duan等 [17] 提出全局分配策略的级联失效模型。郝羽成等 [18] 提出过载级联失效模型，并指出网络节点超出一定容量后并不会失效而是处于过载状态。刘苗苗等 [19] 为实现加权网络的准确划分，发现真实的社区结构，提出一种基于模块度和共邻节点相似性的层次聚类社区划分方法。

综上所述，现有级联失效的研究中，很少有对节点属性的相似性进行研究，本文结合节点之间的相似性，提出了一种新的级联失效策略，此策略可以显著增强网络的鲁棒性，对进一步研究供应链网络的级联失效具有很强的实用性和现实意义。

2. 级联失效模型

2.1. 共邻节点相似度

相似度表示两个对象之间的相似性或相关性，其值通常在0到1之间，其中0表示完全不相似，1表示完全相同。

在复杂网络 $G=\left(V,E\right)$ 中，V表示顶点集合，E表示边的集合。在复杂网络中，同样需要描述两个节点 $i,j\in V$ 的相似性，为了简单起见，本文考虑无向图的场景。两个节点的相似度越高通常表示它们在某种特定的度量或标准下更接近或更相似 [20] 。可以用以下的几种指标进行度量。

1) 共同邻居相似度(Common Neighbors Similarity)

对于两个节点 $i,j\in V$ 而言，如果它们的共同邻居数越多，表示它们的相似度越高，反之，相似度越低。

$CN\left(i,j\right)=\left|N\left(i\right)\cap N\left(j\right)\right|$ (1)

其中， $N\left(i\right)$ 表示节点 $i\in V$ 邻居的集合。

2) 所有邻居相似度(Total Neighbors Similarity)

类似地，将节点i和j的邻居求并集，也可以得到一个指标：

$TN\left(i,j\right)=\left|N\left(i\right)\cup N\left(j\right)\right|$ (2)

3) Jaccard相似度(Jaccard Similarity)

Jaccard相似性系数是衡量两个节点的共同邻居节点占它们总邻居节点的比例，这是一个更广泛使用的相似性度量。如果将两个节点i和j的邻居分别作为两个集合 $N\left(i\right)$ ， $N\left(j\right)$ ，式(3)就可以作为顶点的Jaccard 相似度指标，其相似度是通过邻居来衡量的。

$J\left(x,y\right)=\frac{CN\left(i,j\right)}{TN\left(i,j\right)}$ (3)

本文采用了Jaccard 相似度(Jaccard Similarity)的计算方法，如果两个节点之间不存在共邻节点，则认为这两个节点没有相似性；如果两个节点之间存在共邻节点，则计算其相似度。

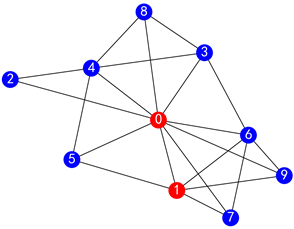
Figure 1. Schematic diagram of BA network

图1. BA网络示意图

例如在图1中，这是一个包含10个节点的BA网络，以节点0和节点1为例，节点1、2、3、4、5、6、7、8、9是节点0的邻居节点，节点0、5、6、7、9是节点1的邻居节点，所以节点5、6、7、9是节点0和1的共同邻居节点，此时，根据式(3)，计算得出节点0和1的相似度为 $J\left(0,1\right)=4/\left(9+5\right)=2/7$ 。

2.2. 级联失效模型

许多研究表明，复杂供应链网络的级联失效模型包括节点初始负载的定义、负载–容量模型和负载再分配策略。

2.2.1. 初始负载的定义

节点i的初始负载 $L_i^0$ 定义为节点的度的函数 [21] 。若与节点i相连的相邻节点数为 $k_i$ ，则节点i的度为 $k_i$ 。本文将节点i的初始负载 $L_i^0$ 定义如下：

$L_i^0=a\ast {\left(k_i\right)}^{\alpha }$ (4)

其中a为负载系数，本文将a设置为1，α为可调参数( $\alpha >0$ )，用于控制网络中节点的初始负载。随着α的增大，不同节点间的负载差异增大，因此，负载分布更加不均匀。

2.2.2. 容量设置及负载再分配策略

节点的最大负载定义为容量 $C_i$ ，与节点的初始负载 $L_i^0$ 成正比，用式(5)表示：

$C_i=\left(1+\beta \right)L_i^0$ (5)

式中， $\beta$ 为可调参数，表示节点的容忍系数，一般 $\beta \ge 0$ ，保证所有的节点不会过载。

初始随机移除节点会触发级联失败。现在假设节点i 发生故障，它的负载将根据优先级规则重新分配给它的邻居，本文采用容量分配的原则，即将其更多的负载分配给容量大的节点，这样每个节点所分

配的负载百分比为 ${\displaystyle \prod j}$ ：

${\displaystyle \prod j}=\frac{C_j}{{\displaystyle \underset{j\in {\Gamma }_i}{\sum }{C}_j}}$ (6)

式中， ${\Gamma }_i$ 为节点i的邻居节点集合，节点j属于 ${\Gamma }_i$ 。根据容量重分配原理，节点j从i接收的附加荷载 $\Delta L_{ij}$ 为：

$\Delta L_{ij}=L_i^0\ast \frac{C_j}{{\displaystyle \underset{j\in {\Gamma }_i}{\sum }{C}_j}}$ (7)

当 $L_i^0+\Delta L_{ij}>C_j$ 时，节点j将失效，网络继续对失效的节点进行负载分配，直到任意节点的容量大于负载时，网络的负载失效才停止。网络的负载重分配的示意图如图2所示。

Figure 2. Schematic diagram of load distribution process

图2. 负载重分配过程示意图

2.2.3. 保留相似度最高的邻居节点的分配策略

基于负载再分配策略，本文提出了一种新的分配策略。具体步骤如下：

1) 选择随机攻击的方式，并将攻击比例q设置为0.1；

2) 根据式(3)计算失效节点与其各邻居节点之间的相似度，并将相似度从高到低进行排序，找出相似度最大的邻居节点；

3) 如果失效节点有两个以上的邻居节点，并且在进行负载分配时会使得相似度最大的邻居节点失效，那么将该节点从邻居节点的集合中删除，且分配 $C_j-L_j^0$ 的负载使得该节点达到饱和状态，后续的负载将不会分配给该节点；

4) 剩余邻居节点按照负载再分配策略进行负载的分配，直至网络达到稳定状态；

5) 计算网络的鲁棒性。

2.3. 级联失效过程

网络的级联故障可以描述为，每个节点具有初始负载 $L_i^0$ 和负载能力 $C_i$ ，在正常情况下 $L_i<C_i$ ，网络处于稳定状态。节点被移除(攻击或机械故障)后，故障节点上的负载将被重新分配给相邻节点。如果邻居的能力不足以处理额外的负载，邻居就会崩溃，从而导致负载重新分配和进一步的过载失败，最终导致整个网络的崩溃 [22] 。级联失效过程的流程示意图如图3所示。

Figure 3. Schematic diagram of cascading failure process

图3. 级联失效流程示意图

2.4. 网络鲁棒性测量指标

攻击一定比例的节点后(本文采用的是随机攻击网络的策略)，网络会发生级联失效。当网络级联失效达到稳定时，失效前后网络中依然存在的有效节点与网络的比值为鲁棒性测量指标。引入G来表示。

$G=\frac{N^{\prime }}{N}$ (8)

其中 $N$ 为节点大小， $N^{\prime }$ 为级联故障停止后网络中仍然有效的节点数。G值高说明级联故障后网络中有效的节点数目多，整个网络的鲁棒性就越好，网络越健壮。

为了避免随机因素对整体仿真效果的影响，本文将代码迭代运行50次，鲁棒性值取50次的平均值。

2.5. 网络种类

为了避免偶然性，本文用以下三种网络类型来对新的策略进行对比仿真实验。

1) BA网络

BA网络(Barabási-Albert网络)由Albert-László Barabási与Réka Albert提出。BA网络模型被用来解释复杂网络的无标度性。常用 $G\left(N,m\right)$ 表示，其中N表示网络中的节点数，m表示新节点与网络中已经存在的m个不同的旧节点连接，生成m条新边。从网络度分布来看，多数节点的度比较小，少数的几个节点具有很大的节点度。它的算法如下：

① 增长：网络从 $m_0$ 个节点开始，并在每个相等的时间间隔增加一个新节点。新节点与网络中已经存在的 $m\left(m\le m_0\right)$ 个不同的旧节点连接，生成m条新边。

② 优先连接：一个新节点与一个已经存在的节点i 相连接的概率为 $P\left(k_i\right)$ ， $k_i$ 为节点i的度，如下式：

$P\left(k_i\right)=\frac{k_i}{{\displaystyle \underset{j}{\sum }{k}_j}}$ (9)

2) ER网络

ER网络(Erdős-Rényi网络)是由数学家Paul Erdős和Alfréd Rény [23] 于1959年提出的一种随机图模型，用于研究随机性连接的网络结构。ER网络通常用G(N, p)表示，其中N表示网络中的节点数，p表示任意一对节点之间建立连接的概率。对于每对节点，以概率p相互连接，以概率 $1-p$ 不连接。ER网络的连接性是随机的，因此具有均匀性，每个节点在连接上没有明显的优势。这与一些无标度网络模型，如BA网络，形成鲜明对比。

3) WS网络

WS小世界网络(Watts-Strogatz小世界网络)是由Duncan J. Watts和Steven Strogatz [24] 于1998年提出的一种复杂网络模型，通常用 $G\left(N,m,p\right)$ 表示。WS小世界网络的生成过程包括两个关键步骤。首先，所有节点按照规则排列在一个环形结构上，每个节点与其相邻节点连接。然后，随机地选择每个节点，以一定的概率p，断开与其相邻节点的连接，并重新连接到环上的其他节点，这个过程称为“重连”。这个概率p控制了网络中的随机性程度。

3. 数值模拟

为了验证提出的新策略能否提高网络的鲁棒性，本文采取随机攻击的方式是进行了数值的模拟仿真实验。实验参数设定如下： $N=500,a=1,q=0.1,m_1=m_2=3$ ，随机网络的连接概率 $p_1=0.012$ ，BA网络中每增加一个节点所加的连边数 $m_1=3$ ，小世界网络的连接概率 $p_2=0.06$ ，且每增加一个节点所加的连边数 $m_2=3$ 重复实验次数 $RE=50$ 。分别在三种不同的网络上进行实验，得出网络在使用新策略前后的鲁棒性变化。仿真结果见图4~8。图中实线为新策略的实验结果。

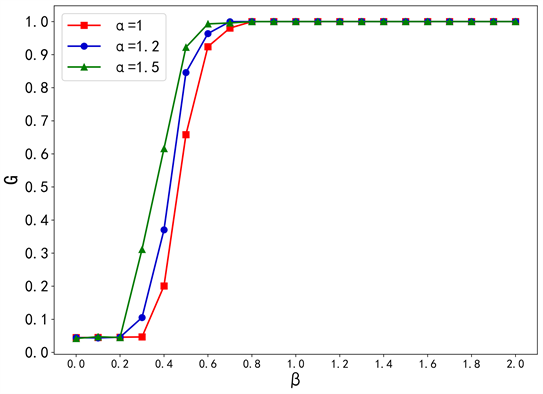
Figure 4. Variation of BA network robustness with α

图4. BA网络鲁棒性随α的变化图

Figure 5. Variation of ER network robustness with α

图5. ER网络鲁棒性随α的变化图

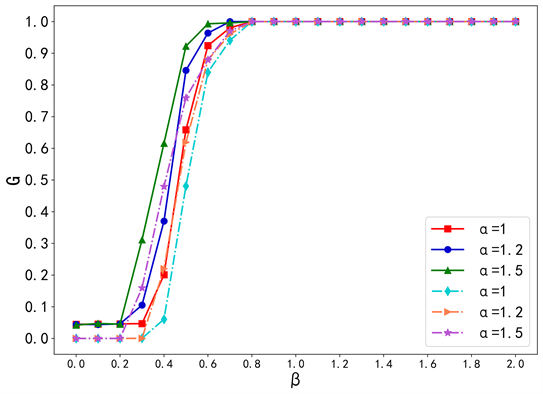
Figure 6. Robustness change before and after the new policy is used in BA network

图6. BA网络中使用新策略前后的鲁棒性变化

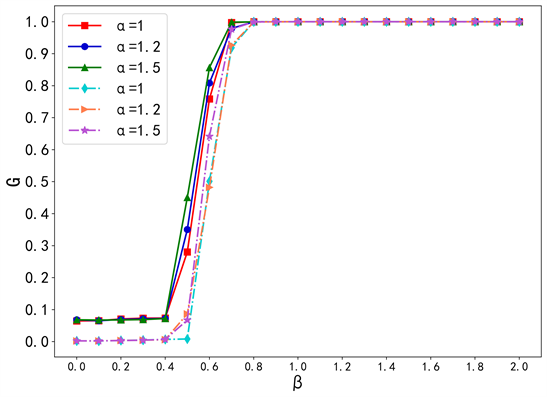
Figure 7. Robustness changes before and after the new policy is used in ER networks

图7. ER网络中使用新策略前后的鲁棒性变化

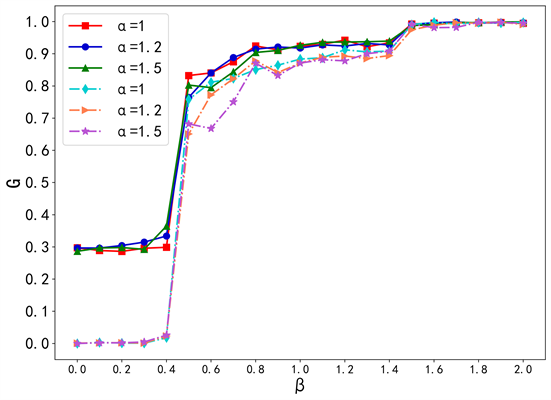
Figure 8. Robustness changes before and after the new policy is used in the WS network

图8. WS网络中使用新策略前后的鲁棒性变化

从图4和图5中可以看出，网络的鲁棒性随着容量参数β 的增大而增大，这是因为大容量节点通常有更多的连接，可以与更多的其它节点进行交互。这使得负载在网络中传播更加高效，并且可以更容易地找到备用路径，以维持网络的连通性。并且，在本文中采用的是按容量比例的重分配策略，所以在负载重分配时，容量越大的节点可以分配到更多的负载，以处理更多的任务。需要注意的是，节点容量增加并不一定总是提高网络的鲁棒性，节点容量的增加也可能会增加网络的复杂性和成本。因此，在设计复杂网络时，需要综合考虑多个因素，合理设置网络的容量参数，以确保网络能够在各种条件下保持高度的鲁棒性。此外，随着负载参数α值从1变化到1.5时，G值时逐渐增大的，即网络的鲁棒性也越大。这是因为当节点的负载参数增加时，通常会分配更多的资源和容量给这些节点，以处理更多的任务或信息。然而，如果节点的负载过高，超出了其资源的处理能力，那么它可能会成为网络的瓶颈，降低网络的鲁棒性。

从图6~8中可以看出，使用新策略的网络鲁棒性明显提高，验证了新策略的可行性。这是因为，当网络中的某个节点发生故障或遭受攻击时，具有相似连接的其它节点可以接管其功能，从而保持了网络的连通性。这种冗余性增加使得网络更能够容忍节点的故障或攻击，这有助于负载在网络中更快速地传播，从而加强了网络的鲁棒性。

4. 结论

本文分析了BA网络、ER网络和WS网络的拓扑结构，描述了由可调参数表征的网络节点负载、容量等网络特性，为了揭示在本文提出的新的策略的条件下，三种网络在遭遇随机攻击时的鲁棒性变化情况，本文在α = 1、1.2和1.5等不同参数下，分别对三种网络进行了仿真实验；同时，本文对使用新策略前后各网络的鲁棒性进行了仿真分析，实验结果验证了新策略的可行性，增强了网络的鲁棒性和稳定性。该结论也为提高供应链网络的鲁棒性提供了理论支撑。在真实的供应链网络中，每个企业都可以看作是一个节点，当某一企业由于各种因素而破产时，会影响到供应链网络中的其它企业，此时，若是保留与该失效企业相似度较大的企业，则可以提高该供应链网络的稳定性和鲁棒性。

然而，在本文的研究中，用Jaccard系数计算节点间相似度的方法准确度有待提高，Jaccard系数不考虑集合中元素的重要性或权重，每个元素在计算中被视为等同。在某些情况下，需要考虑属性的权重才能更准确地反映节点之间的相似性，所以接下来考虑连边权重是一个重要的方向。