1. 引言
在轨道交通运行过程中,由于车辆长时间行驶,在钢轨表面会出现波浪状不均匀的磨损,称为轨道波磨,简称波磨。在波磨路段,汽车行驶时容易产生剧烈的振动和撞击,使得部分零件共振,造成车辆损坏,甚至造成列车脱轨。不仅会影响列车的运行,造成巨大的经济损失,而且还会给旅客的生命安全带来严重的危害。在轨道交通的发展中,波磨严重影响了列车运行的安全性与稳定性 [1] [2] 。鉴于波磨的潜在危害,对钢轨波磨检测进行全面的研究至关重要。
稀疏表示方法,一种新的故障检测方法,成为了国内外学者研究的热点。Huo和Yu [3] 引入一种基于重加权最小化非凸性惩罚正则化项lq (R-WMNPlq)算法的脉冲步冲击字典,对滚动轴承的初始故障诊断;Feng和Liang [4] 提出了移位不变K-means奇异值分解字典(SI-KSVD),提取行星齿轮箱信号的潜在构成分量;Cui等人 [5] 提出了改进的双字典匹配追踪(DMP)和Lempel-Ziv复杂度指数(LZC),用于滚动轴承内圈和外圈故障诊断;周等人 [6] 引入了一种新的移位不变字典学习方法(SIDL),提取故障滚动轴承的周期脉冲;陈等人 [7] 利用自适应字典稀疏提取脉冲(Spa-EIAD),对齿轮箱的脉冲分量进行检测;苏州大学城市轨道交通学院机械故障诊断课题组樊薇等 [8] ,在轴承、齿轮等微弱故障特征提取中,成功地应用了稀疏表示算法。
大量的稀疏表示方法及其改进算法被用于故障诊断领域中,取得了明显的成果,能够很好地识别和提取机械零件中的故障。尽管稀疏表达法具有不可忽略的优点,但是它也有其不足之处,主要在于传统的稀疏表达法常常低估了信号的峰值,而实际情况是,峰值中可能含有更多的周期脉冲信息且应在稀疏系数中应当保持较大的权重。针对稀疏分解的不足之处,本文将对其进行改进,使得故障特征的提取效果更理想。
本文以轨道故障诊断为核心,采用稀疏表达法进行故障特征的提取与分析,并在此基础上对传统的稀疏表达算法进行了改进,从而使故障特征的抽取更加精确。本文采用基于GMC惩罚函数的稀疏表示法,对轨道进行故障特征的提取,以达到对轨道进行故障诊断的目的,并与目前最常用的采用L1范数作为正则化的方法做比较,对比在重构信号方面的表现。
2. 动力学建模与稀疏表示理论
2.1. 轨道波磨简化模型
由于轨道波形磨损是一种周期性的垂直非平顺现象,因而可以用谐波函数来近似地描述轨道波磨 [9] 。由于波形的变化,如果仅考虑一种波长,可以用单一的谐波函数来表示,如图1(a)所示;如果考虑多种波长,则可用多谐波函数描述,如图1(b)所示。
 (a) 单一谐波 (b) 多谐波
(a) 单一谐波 (b) 多谐波
Figure 1. Simplified model of harmonic excitation
图1. 谐波激扰简化模型
单谐波函数表达式为
(1)
多谐波函数表达式为
(2)
式中,L为波磨波长;a为波磨波深;
;n为激扰波数。
2.2. 列车集总参数简化模型
为了更好研究波磨对轴箱引起的振动的影响,需要建立列车集总化参数模型。由于簧上部分引起的轴箱振动冲击不明显 [10] ,所以对列车簧下部分进行分析。建模型如图2所示。
图2中,车体部分与轴箱部分用一个有刚度有阻尼的二系簧相连接,轴箱与轨道用具有刚度的一系簧连接,将轨道与支撑部分看作一个有刚度有阻尼的单自由度系统。设车速为υ,簧下质量为m1,静态下轮对垂向位移为z1,一系簧的垂向刚度为k1,钢轨质量为m2,轨道垂向刚度为k2,轨道阻尼为c2,静态时轨道垂向位移为z2,并规定向下为正方向。在车速为υ时,轮轨的垂向动力学方程为
(3)
假设轨道存在波磨,设为η,则轨道静平衡位移变为z2 + η,车速为υ时,轮轨的垂向动力学方程如下
(4)
对上式进行常微分方程求解,可得
(5)
式中,
;
;
为轴箱加速度。
以单谐波波形为例,对式(1)进行拉氏变换
(6)
为获得响应z1和
,在激励η(s)下,令
(7)
对式(5)进行拉普拉斯变换,并将式(7)代入计算得
(8)
联立以上各式有
(9)
在零初始条件下,
的拉氏变换为式(10)
(10)
式中,
、
、
、
、
均大于零,再由劳斯判据可将式(10)写为:
(11)
式中,
为常数,大小由ω1、ω2、k1、k2确定。
对式(11)做拉氏反变换得
(12)
式(12)为建模结果,
是与频率无关,
是稳态值,故轴箱加速度
与轨道波磨
的频率ω相同,所以可以用轴箱振动信号对轨道波磨进行检测。当列车的行驶速度为
时,轨道存在波磨,波长为λ,则波磨的频率为
,轴箱的响应频率为
,因此知道车速和轴箱响应频率,即可求出波磨波长。
2.3. 稀疏表示模型
稀疏表示的基本思想可表示为:
(13)
式中ai表示过完备字典A中的第i列元素,在稀疏表示中也被称为字典中的第i个原子,ci是稀疏表示系数,稀疏优化算法的目的就是要寻找最稀疏的ci来表示信号x。
稀疏表示的模型示意图如图3所示。
稀疏表示模型在信号处理,故障诊断领域得到了广泛的应用 [11] 。其核心思想是通过目标信号在过完备字典下具有的稀疏属性实现信号的分解与重构。稀疏表示模型具有良好的抗噪能力和微弱状态成分提取能力 [12] ,现有稀疏表示模型一般形式如下。
(14)
其中,λ > 0,y为观测数据,A为字典,c为待估稀疏向量,P(c)为罚函数,λ为正则参数 [13] 。
3. 基于GMC罚函数的稀疏表示方法
在强噪声干扰下对轻微故障特征进行提取与诊断时,信号稀疏表示方法是一种效果极佳方法,采用L1范数作为正则化的方法(即BPD算法),是目前信号处理和特征提取中最常用的一种,便于引导信号的稀疏性,在此基础上构建的函数模型是凸性的,通过快速算法迭代易得到整体的最优解。然而,基于BPD算法容易低估重构信号幅值,可能会造成较大误差,影响检测结果。因此,非凸性质函数作为正则项的方法也被广泛应用,不仅可对幅值较高的信号精准计算,还可以使生成出的故障特征更为稀疏,增强信号特征。
GMC惩罚函数是一类具有非凸性质的函数,能够保证整个目标函数是凸的,其自身的特性能够解决传统BPD算法求解过程中对幅值计算不准确的问题,又能够更大程度地加强信号特征的稀疏性。
3.1. GMC罚函数
GMC罚函数是一种特殊的稀疏性诱导非凸罚函数,在特定情况下,保证构建的稀疏表示目标函数为凸函数,并通过凸优化算法,优化目标函数,从而获得最优解。
GMC罚函数
定义为
(15)
式中,SB是广义Huber函数(Generalizedhuber function),定义为
(16)
3.2. 建立目标函数与保凸性证明
针对故障振动信号稀疏表示的应用,将除故障瞬态成分之外的所有成分统一归为干扰成分是常见被采用的稀疏表示建模方式,故障振动信号
建模为
(17)
式中
为故障瞬态成分,
为干扰成分。
根据波磨故障信号的特点,将故障信号按式(17)进行建模,包括故障瞬态成分和噪声干扰成分两部分。基于GMC罚函数,将非凸正则化最小二乘目标函数定义为
(18)
接下来,需要分析并确定GMC正则化目标函数为凸函数的条件,将上式重写为
(19)
式中,P = BTB,
是在x上的仿射,
是关于x的凸函数,是一组关于x的凸函数的逐点最大值。因此,目标函数
为凸函数的条件为
(20)
相应地,矩阵B需满足以下条件,即
(21)
3.3. 构造离散傅里叶变换字典
为了稀疏地表示啮合振动信号部分,本文取变换字典A1为归一化的K点离散傅里叶变换(DFT)的逆变换,K ≥ N,N为待变换信号的长度。信号左乘字典A1就是对其做DFT变换的逆变换。定义
为:
(22)
式中,DFTK是长度为K的补零的离散傅里叶变换,乘子
用于A1的归一化,使得
,由于K ≥ N,为了符合信号长度N,本文取字典A1为K点DFT逆变换的前N行。
定义
为:
(23)
式中,长度为N的向量x将在进行DFT变换前补零至长度K。
字典A1每一列向量的L2范数均相等:
(24)
相比于其他分析字典,变换字典的特点在于字典本身并不是一个含有真实元素值的矩阵,而是一种变换,DFT字典有ATA = I这一性质简化了运算过程,减少了计算量,也节约了存储空间。
3.4. 求解算法
通过最小化GMC正则化最小二乘目标函数式(18),可以得到最优稀疏表示系数Copt。最小化目标函数可写为一个鞍点问题:
(25)
式中
定义为
(26)
利用前向后向分裂(FBS)算法求解鞍点问题。为了得到Copt,
分解为
(27)
(28)
(29)
基于FBS获得Copt如下流程,进一步地,
(30)
(31)
式中,μ为常数,且满足如下条件
(32)
式中,A满足紧框架条件ATA = I。在实际应用中,γ通常设置为0.5 ≤ γ ≤ 0.8。
类似地,基于FBS获得Vopt的迭代流程如下
(33)
(34)
式(31)和(34)中,soft为软阈值函数,具体定义为
(35)
式中,T为阈值。
基于上述求解流程,得到了GMC正则化稀疏分解算法,如表1所示。

Table 1. GMC regularized sparse decomposition algorithm
表1. GMC正则化稀疏分解算法
3.5. GMC罚函数与L1罚函数信号重构的效果对比
根据第二章轨道波磨动力学研究,仿真信号建模如式(36)所示。
(36)
参数设置:D = 1.8,f = 2000 Hz,ψ = π/6,
是与频率无关,得到的仿真信号图4如下所示。
其中图(a)为故障信号,图(b)为噪声信号,图(c)含噪复合信号。接下来利用基于L1范数作为惩罚项的稀疏分解方法,构造DFT字典,利用前向后向分裂算法(FBS),求解稀疏表示目标信号并重构,得出重构信号如下图5所示。
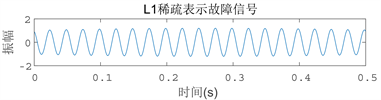
Figure 5. L1 sparse representation of fault signal
图5. L1稀疏表示故障信号
然后控制变量,在其余条件不变的情况下,只改变稀疏表示信号中的L1罚函数,将其代替成GMC非凸罚函数,其信号效果如下图6所示。
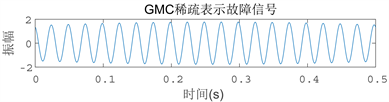
Figure 6. GMC sparsely represents fault signal
图6. GMC稀疏表示故障信号
RMSE利用观测值同真实值之间的差异表明测量数据背离实际数据的程度,RMSE值越大说明对于原始信号的重构能力越差,值越小,重构性能越好。其计算表达式如式(37)所示
(37)
式中,x表示仿真的无噪齿轮瞬态信号,
表示采用所提方法的提取的齿轮瞬态信号,N表示信号的长度。为了比较不同罚函数的提取效果,本文采用L1范数正则化和GMC非凸罚函数的稀疏表示方法对仿真信号进行了分析,需要量化分析两种重构的表现。故采用均方根误差来实现,衡量重构与原始信号之间的偏差,有效的将信号重构表现量化,进行客观对比。
信噪比(SNR)又称讯噪比,反映了噪声对信号的干扰程度,计算表达式如下:
(38)
式中,P为平均功率。信噪比愈高,则信号中的干扰愈少。以dB作为计量单位,则信噪比的计算表达式可定义为:
(39)
以典型的波磨信号为例(图5、图6),将在L1罚函数条件下重构信号的RMSE记作RMSE(L1),将在GMC罚函数条件下重构信号的RMSE记作RMSE(GMC)。该仿真含噪信号的信噪比(SNR)为−5.8549 dB (信噪比表示噪声的影响,噪声越小,信噪比越大),RMSE(L1) = 0.4730,RMSE(GMC) = 0.1679。
经过多组含噪复合信号分别在L1与GMC罚函数上重构信号,得到多组RMSE的数据,可以得出:
(40)
由此可见,GMC罚函数在信号重构方面的性能更好,优于L1罚函数。
4. 工程试验分析
为了使得实验结果更为准确,仿照轨道振动信号的特征,通过含噪的实测信号进行实验。基于GMC范数正则化的信号稀疏表示从噪声中提取正常段信号与波磨段信号,进行信号分析对比,验证方法的有效性。
4.1. 数据分析
从数据库中采集一段在实验轨道上实验的振动信号:车辆运行时速为68 km/h,采用长度为1060采样点的窗口长度对1 km的信号进行逐段分析,每次平移长度为530个采样点,对应的铁轨长度为5 m。
用GMC稀疏表示得:
(41)
采集的数据,左侧轨道与右侧轨道相似,以右侧段为主要实验对象,针对正常区段和波磨区段分别取1 s信号进行稀疏处理,得到的结果如图7,图8所示。
对比正常段信号和波磨段信号处理后的结果,明显发现波磨段信号时域幅值冲击更加明显且高于正常段,波磨段信号幅值冲击频繁且频率段能量集中在66 Hz与77 Hz附近,与正常段对比认为该频率为波磨频率ω,根据波长公式
,求得对应的波磨长度为245~286 mm附近。观察图7与图8,两段信号的稀疏表示处理后的时域幅值有较大差异,故考虑将最大幅值作为判断波磨信号与正常信号的依据,结合其频域分布实现波磨的故障诊断。
通过两段信号在时域频域上的幅值表现,预设幅值最大阈值为7。通过以上操作,我们可以假设如果信号稀疏表示的最大幅值超过阈值且频率集中在66~77 Hz之间,则判断该段为波磨段,反之则为正常段。进一步的,通过分析可能存在波磨故障的区段信号频谱,判定该段是否存在波磨故障。

Figure 7. Normal segment signal processing
图7. 正常段信号处理

Figure 8. Corrugation section signal processing
图8. 波磨段信号处理
整套波磨故障诊断流程如图9所示。
4.2. 信号实测
在上一小节采集的实验轨道数据中,以右侧轨道为例,取200米长的轨道信号,为保证实验结果的准确,需要进行40次模拟实验,每次平移530个采样点。每10米长为一组,为保证实验的准确性,需要在下一组设置重叠部分,每一组的前五米与上一组的后五米相同,从而保证实验数据的连续性,减少漏检的可能性以及分组带来的误差。
以典型的波磨信号为例,如图10所示。
此段信号的稀疏表示最大幅值超过阈值且频域集中在74 Hz,符合上文对于波磨特点的分析,故可以判断该区段为波磨段。通过对四十组信号同理分析,得出200米长的信号所存在的波磨区间。
经过四十组的信号分析,波磨故障诊断结果如表2所示。

Table 2. Fault diagnosis results of corrugation
表2. 波磨故障诊断结果
将检测的波磨理论数据与实际波磨数据进行对比分析,后200 m中实际波磨长度为800 m~861 m,共计61 m,经检验出的波磨长度为51 m,本次实验检测的准确率为83.61%,基本验证了方法的有效性,但仍有部分错误检测,精确度有待提高。
在实验过程中,出现了一些误检的现象,对此问题进行详细分析,发现检测信号处理时认为列车以68 km/h的速度保持匀速前进,但实际上列车的速度存在小范围的波动,无法保持绝对精确的匀速前进,因此导致处理时会产生误差;且实验过程中的噪音不能完全去除也会对实验结果有一定的影响;车辆行驶在钢轨上,经过钢轨接缝处时可能会造成一些冲击误判等。
5. 总结
本文以轨道波磨为研究对象,进行动力学建模,建立列车集总参数简化模型推导波磨状态下的列车振动信号,研究其故障信号产生机理,对故障特征加以分析,得出以下总结:
1) 基于信号稀疏表示基本原理,根据信号分量的不同特征,构造不同的变换字典,求解目标函数,完成对故障成分和稳态成分的提取和重构,开展仿真,对比了L1范数正则化和GMC非凸罚函数的稀疏表示方法对仿真信号的效果,得出GMC罚函数在信号重构方面的性能更好,优于L1罚函数。
2) 基于GMC罚函数的稀疏表示法进行工程实验,分析重构信号的时域图和频谱图,得出故障特征,判断波磨位置,验证了所提方法的有效性并针对实验结果的不足之处加以分析。
参考文献