1. 引言
随着空间光学遥感器的发展,需要采用机械制冷机对核心部件进行控温成为常用手段。机械制冷机的在轨工作是在轨微振动的主要来源,且制冷机的振动主要集中在50 Hz、60 Hz等低频频段 [1] [2] 。同时微振动会引起相机光学元件产生刚体位移和面形变化,从而影响相机的在轨光学成像品质 [3] 。常见的减隔振手段主要有隔振、吸振、阻尼减振等。考虑到发射时的力学环境约束,常规减振结构只能对中高频振动产生减振效果,无法满足低频减振的效果。
针对以上问题,国内外科学家探索利用负泊松比超材料和局域共振超材料来解决对低频隔振、高支承刚度的需求问题。具有负泊松比效应的超材料通常表现出轻质、高阻尼、吸声、隔热等物理特性 [4] 。其功能基元的拓扑型式包括蜂窝结构、点阵结构、旋转刚体结构、手性结构、穿孔板以及节点–纤维结构等 [5] 。由内六角蜂窝胞元构成的负泊松比超材料在船舶中的减振方面已经得到了很广泛的研究与应用。杨德庆 [6] 通过将负泊松比超材料应用到浮筏的设计,得到具有轻量化、高隔振效果、高降噪性能的浮筏,与传统的常规平板式浮筏相比,轻量化超材料浮筏在发动机的工作频率为15 Hz能够实现4 dB的振级落差增益,同时减重达37.65%。然而其质量过重,仍然无法满足空间制冷机隔振结构对轻量化的需求。吕亦乐 [7] 针对变形镜的减振需求,用ABS为材料的二维与三维正弦曲线超材料实现了1000 Hz以下的减振,不过其支承刚度无法满足空间制冷机的要求。Zhengyou Liu [8] 等人在2000年首次提出局域共振超材料的概念。而针对弹性波的衰减效果,尽管研究人员目前探知了增大振子质量 [9] 和增大振子数目 [10] 这两种方法来增大对弹性波的衰减效果。戴隆翔 [11] 、江山 [12] 、廉紫阳 [13] 等人,利用压电材料产生局域共振带隙,抑制了超精密运动平台的微振动。赵亚平 [14] 针对光学载荷的微振动抑制要求,运用电磁式动力吸振器实现最大抑制达37.3%。
本文针对空间制冷机微振动抑制所需的低频、高刚度的要求,基于正弦曲线负泊松比超材料,通过增加谐振子的方式,设计了含谐振子的负泊松比超结构,给出了使其满足低频隔振需求。
2. 制冷机隔振需求
2.1. 制冷机隔振需求分析
空间用制冷机主要指常用的脉冲管和斯特林制冷机,其微振动主要来源于其内水平对置压缩机的微振动,虽然冷指部分也会有微振动,但轻量级较小,对空间相机的影响可以忽略。由于压缩机活塞在制造和安装等过程的不对称,导致其不可避免的存在振动输出 [15] 。且其输出的振动力是以驱动频率为基频的一系列谐波,主要表现在基频及其二倍频、三倍频上,如图1所示。同时该谐波主要出现在水平方向,即制冷机主要表现为水平方向的微振动。
微振动不会对包括制冷机在内的航天器内结构及元器件造成结构破坏,但对于高精度航天器而言,微振动将造成姿态稳定度或指向精度的下降,需要加以抑制 [16] 。其对空间相机的主要影响是指其会造成成像质量的下降。通常情况下,当相对像移量达到0.5像元时,像质将明显退化达到不可接受的程度。
驱动频率为44 Hz的脉冲管制冷机,要求在44 Hz、88 Hz、132 Hz这三个频点微振动量级小于0.8 N。
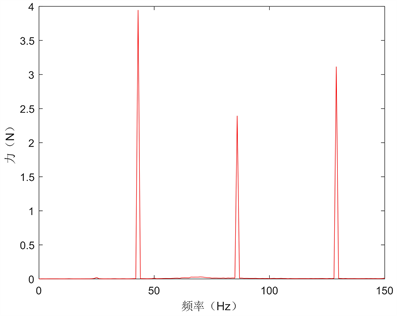
Figure 1. Microvibration frequency domain curve of 250 w pulse tube refrigerator
图1. 250 w脉冲管制冷机微振动频域曲线
2.2. 制冷机隔振结构性能评价方法
目前常用的隔振效果评估指标有力传递率、插入损失、振级落差、功率流等。一般以力传递率作为隔振效果的理论预测依据。但是对于实际效果的测定,由于力传递率是不易测量的,因而通常采用插入损失或振级落差来评定各种实际系统的隔振效果。
本文采用插入损失IL的方式来进行结构减振性能的评价。插入损失定义为被隔振设备振动响应的有效值与对应基础响应的有效值之比的常用对数的20倍。本文利用结构最下方所有结点的支反力来计算隔振结构的插入损失。其表达式为:
(1)
式中:
为结构的插入损失;
、
分别为被隔振结构无隔振时传递到基础的支反力和被隔振结构有隔振时传递到基础的支反力。
值越大,代表隔振结构的隔振效果越好;当
值出现负数时,代表结构对振动不仅没有抑制作用反而因为共振等现象造成振动的放大。在本文中,当微振动量级小于0.8 N,隔振效率优于80%时,需满足
≥ 14。
3. 二维负泊松比结构设计与隔振性能分析
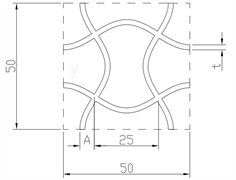
本文中所采用二维正弦曲线超材料胞元如图2(a)所示。二维结构由8个二维正弦曲线胞元构成,如图2(b)所示。
 (a)
(a)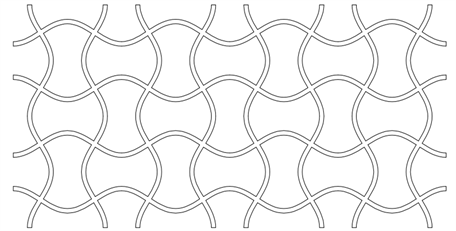 (b)
(b)
Figure 2. Metamaterial cell and structure diagram [8]
图2. 超材料胞元和结构图 [8]
正弦曲线的周期为50 mm,胞元幅值A为5 mm。
所使用的正弦曲线的基本方程为:
(2)
该结构的整体尺寸为200 × 50 × 100 mm。图1中的t为胞元的壁厚。
为了验证将负泊松比超材料结构应用于制冷机的减振结构的效果,通过有限元方法,分析结构的固有模态和频率响应。减振结构和制冷机的模型如图3所示。
结构采用铝合金材质,其弹性模量E = 70 GPa,泊松比
= 0.33,密度
= 2700 kg/m3。为模拟外形尺寸,采用600 mm×600 mm×10 mm的板作为工装,并附加20 kg的质量来模拟制冷机的实际重量以及支撑工装的尺寸以及重量。结构的下方将6个自由度全部约束。
由于胞元的周期、幅值A和胞元的壁厚t均会对结构的隔振效果产生影响,可通过参数分析方法精确设计出满足减振效果要求的结构。为简化参数分析问题的求解,本文在胞元的周期、幅值A不变的情况下,仅针对壁厚t这一参数进行频响分析。t的取值范围:0.36 mm ≤ t ≤ 0.40 mm。
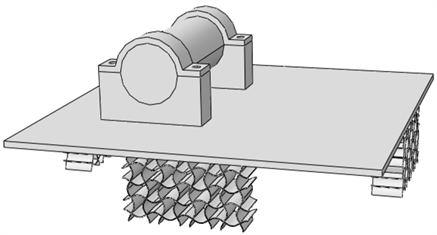
Figure 3. Vibration isolation structure model
图3. 隔振结构模型
对板结构上的中心点施加一个简谐激励并与板的四个角进行运动耦合;并将底部所有点耦合于底部的中心,将底部固定,并采集底部的支反力作为结构隔振性能的评价点。同时,频响分析时采用模态叠加法,并赋予结构阻尼5%。为便于比较分析频点处的隔振效果,在频点采用10 N的水平激励,其余频率段无激励的分析方法,以此来获得更清晰的用于分析隔振效果的曲线,其结果如图4所示。
图4. 二维结构的参数分析结果
从图4所示的分析结果中可以清晰的看出,当只在所需的隔振频点给予激励时,结构能够对激励起
到一定的减振效果。由于机械系统的隔振频率需大于
,因此刚度越低,系统的隔振刚度越好。
同时为了保证结构的支承刚度,在选取的t值范围内,当t的值为0.36 mm时隔振效果最优。同时由于壁厚t的值会对结构的共振频率有很大的影响,如图5所示。
图5. 结构的共振频率
从图5的结果可知,当t变小时,结构的共振峰将向低频移动,会减弱结构在主动段的承载能力,为此无法通过减小壁厚的方式,增强结构在44 Hz这一频点隔振效果。
当t = 0.36 mm时,在44 Hz附近的隔振点的减振性能,IL = 8.95,在88 Hz这一频点的IL = 23.12,在132 Hz这一频点的IL = 29.43。
通过以上的分析可以得出,当t = 0.36 mm时,结构在88 Hz以及132 Hz能够实现80%以上的隔振性能。因此后续的设计将集中在提升44 Hz隔振点的隔振性能。
4. 含谐振子的二维负泊松比隔振结构设计
4.1. 谐振子胞元设计与带隙理论
添加有谐振子的胞元由基体、弹性体以及散射体构成。散射体与弹性体构成类似动力吸振器,基于局域共振机理,弹性波频率接近散射体的共振频率时,弹性波的能量会被散射体吸收,从而产生隔振带隙 [17] 。
图6. 谐振子胞元结构
本文以二维正弦曲线负泊松比胞元为基体,在单胞内添加相同材质的散射体和弹性体。谐振子结构的单胞结构如图6所示,散射体长度ls,散射体宽度为bs,厚度为hs,弹性体采用铝板制成并根据梁的挠度得到等效刚度,铝板的长度为lt,散射体宽度为bt,高度为ht。
根据梁的挠度公式:
(3)
式中:F为梁自由端所受的力,l为梁的长度,E为梁的弹性模量,I为梁的截面矩。
根据矩形截面的截面矩计算公式:
(4)
式中:b为梁的宽度,h为梁的高度。
得到等效成弹簧的刚度k的计算公式为:
(5)
根据机械系统中共振频率的计算公式:
(6)
式中:f是共振频率,k是系统的弹性系数,m是系统的质量。
得到隔振频率:
(7)
并且因为等效质量密度为负值的频率区间也被认为是晶格超结构的带隙范围 [18] ,所以当
处于
和
之间时,结构能够产生隔振带隙,或隔振带隙落在此
所对应的频率。即隔振带隙在
和
之间,其中m为散射体质量,M为基础胞元质量。
4.2.隔振结构隔振效果分析
由于含谐振子的隔振结构减振性能受到多个因素的影响,同时由于基础负泊松比胞元的刚度会对谐振子的弹性体刚度产生影响,因此,在考虑胞元内所能嵌入的散射体体积的前提下以及满足隔振效率的条件下,利用仿真软件Nastran进行基于模态分析和频响分析的参数分析,得到符合要求的尺寸与结构。同时,由于分析的时候同样不需要计算六个方向上的应力,所以有限元分析时隔振的负泊松比结构依旧使用壳单元的同时,弹性体与散射体也采用壳单元结构。
由谐振子胞元隔振机理可知,含有谐振子的减振超结构的带隙频率与谐振子的固有振动特性相关。同时由于谐振子的质量较低,其隔振频带依旧较窄,应尽可能使得其固有振动频率接近需要隔振的频点。最终结合仿真结果,确定ht = 10.1 mm,bs = 0.41 mm。
为了对含谐振子的负泊松比超材料结构进行隔振效果验证,对整体结构进行频响分析。得到的频响分析结果如图7(a)和图7(b)所示。力的施加方式以及评价点的选择与基础结构的频响分析相同。隔振效果验证包括两部分:一是10 N的激励,其结果如图7(a)所示;二是在频点采用10 N的水平激励,频点附近1 Hz范围内的采用1 N的激励,其余频率段采用10−3 N大小的激励,以此来获得更清晰的用于分析隔振效果的曲线,其结果如图7(b)所示。除此之外,为了体现谐振子的减振效果,将二维结构的结果与图7(b)所得到图像进行对比分析得到图7(c)。
 (a)
(a) 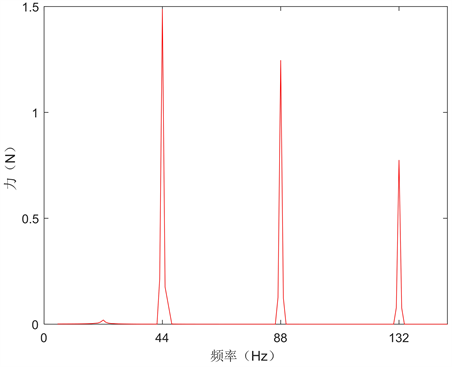 (b)
(b)  (c)
(c)
Figure 7. The results of the frequency response of the resonant structure and the comparison with the two-dimensional structure
图7. 含谐振子结构的频率响应结果以及与二维结构的比较结果
从图7(a)所示的分析结果中可以清晰的看出除了基础负泊松比结构所导致的共振峰外,还会在44 Hz之后出现新的共振峰,该共振峰是由于引入谐振子后形成的,该共振峰的形成表明谐振子的引入不仅会减小44 Hz这一频点的振动,同时会影响88 Hz以及132 Hz这两个频点的隔振。
从图7(b)以及图7(c)所示的分析结果中可以清晰的看出,当只在所需的隔振频点及一定带宽内给予激励时,结构能够对激励,尤其是相比于基础负泊松比结构在44 Hz这一频点上的激励起到更好的减振效果。为了量化增加谐振子的二维负泊松比隔振结构的减振效果,利用插入损失来评价结构的减振性能。
在44 Hz附近的隔振点的减振性能,IL = 16.55,在88 Hz这一频点的IL = 18.09,在132 Hz这一频点的IL = 22.22。
通过以上的分析可以得出谐振子的引入能够很好的提升在44 Hz的隔振效果,使得结构在44 Hz、88 Hz以及132 Hz均能够实现80%以上的隔振性能,满足隔振需求。
5. 结论
本文针对二维正弦曲线负泊松比超结构添加谐振子的微振动抑制效果进行了研究,通过合理设计谐振子弥补了二维正弦曲线负泊松比结构在某一个或某几个频点隔振能力的不足,使得含有谐振子的二维正弦曲线负泊松比隔振结构能够同时满足基频、二倍频及三倍频的隔振效果优于80%。得到以下的结论:
1) 添加谐振子能够提高所需要的频点的隔振效率,即制冷机基频的振动能够得到更有效的隔离,其减振机理属于局域共振减振;
2) 在一定范围内,谐振子质量越大,在对应频点的隔振效果越好;
3) 谐振子所引入的共振峰会使得二倍频及三倍频的隔振效果减弱,不过通过合理设计可以使其依旧能够满足隔振效果优于80%要求。