1. 引言
随着现代显示技术的不断发展,高效节能的自激活发光材料已成为新型发光材料研究的焦点。新型发光材料主要包括磷酸盐、砷酸盐、硼酸盐、钨酸盐、硅酸盐、钼酸盐等体系 [1] [2] [3] [4] [5] 。自激活荧光粉具有高热化学稳定性、光致发光特性和高荧光量子效率,使其在家庭照明、发光器件、光电器件和颜料等领域具有广阔的应用前景 [6] [7] [8] 。
自然界中具有丰富的钼元素,金属钼酸盐由于具有优异的氧化还原性能、适中的带隙值、较短的离子扩散路径、抗腐蚀性等受到研究人员的广泛关注。在金属钼酸盐中,白钨矿钼酸盐尤其值得注意,它的化学式为MMoO4,其中M代表二价阳离子(Pb2+、Ca2+、Ba2+、Sr2+、Mg2+和Cd2+等)。在这种结构中,二价金属M离子和钼离子分别与8个氧原子和4个氧原子进行配位。白钨矿钼酸盐除了在荧光粉、光催化领域的应用外,在传感器、光纤传导、闪烁体、磁体、储能器件等领域也有应用。
在钼酸盐中,MgMoO4由于其作为可调谐固体激光晶体的潜在应用而受到关注 [9] 。常压条件下,MgMoO4具有两种结构,一个是三斜晶系 [10] ,对应α-MgMoO4(Pī);另一个是单斜晶系 [11] ,对应β-MgMoO4(C2/m),这两种结构中Mo都是四面体配位。在
中,基态Mo6+的外层轨道被电子填满(s²p²),当其被一定能量的光子激发时,O2−中2p轨道的电子受激发后,向Mo6+的4d轨道跃迁,随即又回到基态,经跃迁辐射发出光子。钼酸盐在近紫外(220~350 nm)区域具有Mo-O宽且强的电荷转移带。因此,关于钼酸盐基材料的光学改性研究备受关注。
大部分的研究通过对样品的表面形貌设计、晶粒尺寸控制以及离子掺杂来调控钼酸盐晶体的光学性质。Spasski等 [12] 报道了不同生长条件下MgMoO4晶体的发光特性并对MgMoO4:Yb3+的发光特性进行了研究,研究表明,Yb3+掺杂MgMoO4导致在红外区出现杂质发光带。对于掺杂Cr3+ [9] [13] 、Yb3+ [12] [14] 、Nd3+ [15] 、Eu3+ [16] [17] 、Eu3+和Dy3+ [18] 、Eu3+和Bi3+ [19] 的MgMoO4晶体,也有一些光谱性质的数据,研究表明,与Y2O2S:0.05Eu3+荧光粉相比,Mg0.80MoO4:Eu3+0.20荧光粉在400 nm附近表现出更强的激发带,并且在394 nm光激发下由于Eu3+ f-f跃迁而增强了红光发射 [17] 。
除此之外,温度和压力也是调控材料结构和性能的有效手段。高温拉曼研究表明,单斜相在293 K到640 K范围内是稳定的。然而,在较高的温度下,晶体经历了两次结构相变,在640 K时从单斜相转变为非公度相,在770 K时从非公度相转变为六方相 [20] 。高压下,原子间的间距会发生变化,晶体结构也会随之发生改变。单晶X射线衍射和高压拉曼的结果都已表明,β-MgMoO4在1.5 GPa以上发生了等结构相变(C2/m→C2/m),成为γ-MgMoO4。压致相变是由两个MoO4四面体的旋转驱动的,伴随着Mo的配位从4个氧原子增加到6个氧原子,Mo离子从四面体到八面体的配位变化 [21] [22] 。晶体结构的改变必然会对其性质产生影响。压力对于β-MgMoO4的光学性质,如复介电性质、吸收谱、反射谱会有什么影响有待进一步的研究。本文采用压力作为物性调控的手段,探究不同压力下MgMoO4的光学性质,对其进行第一性原理的计算,为以钼酸盐为基础的发光器件改性和应用提供思路和理论参考。
2. 模型与计算方法
2.1. 理论模型
在MgMoO4晶体的计算中,β-MgMoO4结构的空间群为:C2/m,晶格参数为:a = b = 6.867553 Å,c = 7.030000 Å,α = β = 101.68849˚,γ = 84.6237˚。γ-MgMoO4结构的空间群为:C2/m,晶格参数为:a = b = 6.537456 Å,c = 7.611 Å,α = β = 107.26796˚,γ = 84.94078˚。表1为0 GPa的β-MgMoO4和相变后1.95 GPa的γ-MgMoO4结构优化前晶体结构的信息。图1是根据文献报道的结构信息建立的晶体结构图。在晶体的计算中,β-MgMoO4结构和γ-MgMoO4结构均采用原胞模型(各含24个原子)。

Figure 1. (a) Crystal structure of β-MgMoO4 at 0 GPa; (b) Crystal structure of γ-MgMoO4 at 1.95 GPa
图1. (a) 0 GPa的β-MgMoO4晶体结构;(b) 1.95 GPa的γ-MgMoO4的晶体结构

Table 1. Crystal structure information of β-MgMoO4 and γ-MgMoO4 [21] [23]
表1. β-MgMoO4和γ-MgMoO4的晶体结构信息 [21] [23]
2.2. 计算方法
本论文采用Materials Studio材料模拟软件中CASTEP (Cambridge Sequential Total Energy Package)模块,基于密度泛函理论,关联泛函使用广义梯度近似GGA下的PBE泛函处理 [24] [25] [26] 。并由采用超软赝势USP [24] 处理价电子与离子实之间相互作用势,对晶胞模型进行结构优化时采用BFGS [27] 算法。优化计算的具体精度参数设置如表2所示。

Table 2. Geometric optimization parameter setting of β-MgMoO4 and γ-MgMoO4
表2. β-MgMoO4、γ-MgMoO4的几何优化参数设置
先对β-MgMoO4、γ-MgMoO4 进行截断能的测试,在得到其收敛后,再进行k点取值的设置。固定截断能取值520 eV,体系计算总能量在k点设置为6 × 6 × 6。参与计算的价层电子轨道组态分别Mg-2p63s2、Mo-4s24p64d55s1、O-2s22p4。
在利用Materials Studio中的CASTEP模块进行晶胞结构优化和光谱性质计算时需进行收敛性测试,以确定优化和计算参数选择的合理性。CASTEP模块本身会根据所选择的赝势、晶胞尺寸等提供预设的参数。本文在0 GPa下计算得到的β-MgMoO4带隙值是3.745 eV,与文献 [21] 在0.87 GPa下计算得到的数据3.58 eV接近,这表明本文的计算结果是可靠的。
3. 计算结果与讨论
3.1. 能带结构、态密度
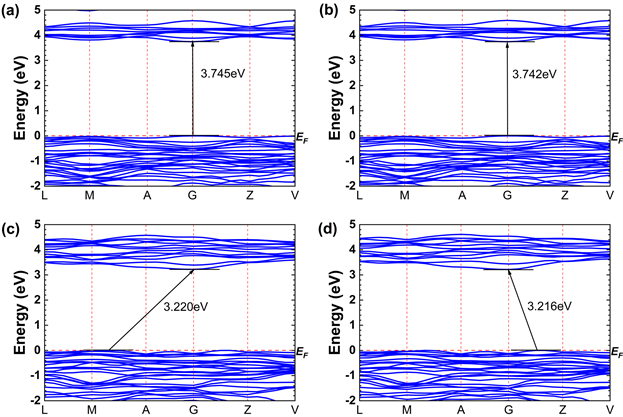
Figure 2. Band structure maps of MgMoO4 under different pressures: (a) 0 GPa-β-MgMoO4; (b) 1 GPa-β-MgMoO4; (c) 2 GPa-γ-MgMoO4; (d) 5 GPa-γ-MgMoO4
图2. 不同压力下MgMoO4的能带结构图:(a) 0 GPa-β-MgMoO4;(b) 1 GPa-β-MgMoO4;(c) 2 GPa-γ-MgMoO4;(d) 5 GPa-γ-MgMoO4
关于电子结构的讨论对理解样品晶体结构和光学性质之间的关系非常必要。MgMoO4在不同压力下的能带结构如图2所示,纵向红色的虚线代表布里渊区的点,横向红色的虚线表示费米能级。图2(a)和图2(b)为β-MgMoO4在0 GPa和1 GPa下的能带结构,其能带属于直接带隙,导带底和价带顶均位于布里渊区的G点。0 GPa时的带隙值为3.745 eV,随着压力的增加,1 GPa时的带隙值减小为3.742 eV。图2(c)和图2(d)为γ-MgMoO4在2 GPa、5 GPa下的能带结构,相变后的γ-MgMoO4属于间接带隙,导带底位于布里渊区的G点,价带顶分别位于布里渊区的M点和A点之间、G点和Z点之间。费米能级同样位于价带顶处。2 GPa下γ-MgMoO4带隙值为3.220 eV,5 GPa时带隙值减小为3.216 eV。比较不同压力下的能带结构,压致相变的同时,能带结构发生了从直接带隙到间接带隙的转变,压力对带隙具有明显的可调控性。
为进一步分析MgMoO4的能带结构,我们对其进行了态密度的计算,结合态密度图和能带结构可以分析不同原子的不同轨道对导带和价带的贡献,以及电子的局域性质和杂化特征。计算结果如图3所示,钼酸盐价带的顶部由氧(O)的2p态和钼(Mo)的4d态组成,导带部分主要由Mo的4d态以及少量O的2p态和Mg的2p态组成。此外,O原子的2p轨道在费米能级附近表现出较强的局域性。MgMoO4的能带间隙是由MoO4基元与Mg2+共同决定的。八面体MoO4氧阴离子络合物被认为是主要构成元素,它定义了低能区域的光学性质。高于费米能级部分的TDOS积分值将反映材料的硬度,TDOS的值越小,材料
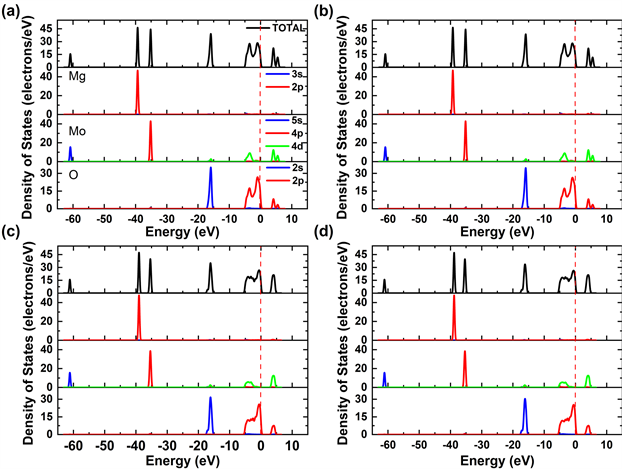
Figure 3. Total and partial density maps of states of β-MgMoO4 at (a) 0 GPa and (b) 1 GPa and γ-MgMoO4 at (c) 2 GPa and (d) 5 GPa
图3. β-MgMoO4在(a) 0 GPa和(b) 1 GPa,γ-MgMoO4在(c) 2 GPa、(d) 5 GPa下的总态密度、分态密度图
的硬度就越高 [28] 。经过测算得到β-MgMoO4在0、1 GPa,γ-MgMoO4在2、5 GPa压力下的TDOS值分别为22.420、22.158、21.225和21.188,这意味着MgMoO4的硬度将随着压力的增加而增大。
3.2. 复介电函数
介电函数与半导体的能带结构及光学性质息息相关。半导体的宏观光学性质可由复介电函数来描述,公式为:
(1)
其中:ω为光的频率,ε1(ω)为介电函数的实部,ε2(ω)为介电函数的虚部。
复介电函数能反映电子跃迁的微观变化,实部表示半导体在外电场作用下的极化程度,实部表征对电荷的束缚能力和电极化能力。图4为不同压力下MgMoO4的复介电函数。当入射光能量E = 0时,介电函数的实部上纵坐标所对应的值称为静态介电常数ε1(0),如图4(c)所示。相变前,0 GPa时β-MgMoO4静态介电常数为2.735;1 GPa时β-MgMoO4静态介电常数为2.746;压致相变后,2 GPa时γ-MgMoO4静态介电常数为3.197,而5 GPa时γ-MgMoO4静态介电常数增加到3.242。由此可见,MgMoO4的静态介电常数随压力的增大而增大,相变后,5 GPa时γ-MgMoO4体系的屏蔽性和对电子的束缚能力最大,极化能力最强,有利于电子空穴对的分离,压力有助于改善材料的光催化活性。
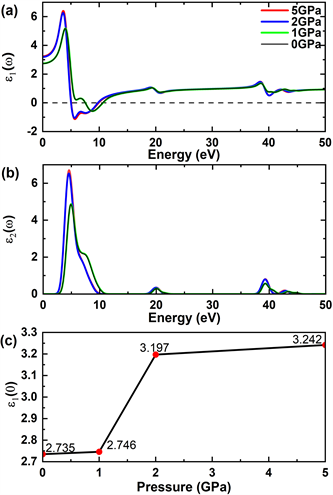
Figure 4. (a) Real parts ε1(ω), and (b) imaginary parts ε2(ω) of the complex dielectric function of MgMoO4 under different pressures; (c) Change of static dielectric constant ε1(0) with pressure
图4. 不同压力下MgMoO4的复介电函数的实部ε1(ω) (a)、虚部ε2(ω) (b);(c) 静态介电常数ε1(0)随压力的变化
介电虚部与态密度分析对比,可以发现介电峰的形成与价带和导带之间的电子跃迁有关。MgMoO4的介电峰主要归因于O-2p轨道的电子向Mo-4d轨道的电子跃迁。由于压力引起的是等结构相变,β-MgMoO4与γ-MgMoO4的电子跃迁过程相似,介电峰形态比较接近。介电虚部表示形成电偶极子所需要消耗的能量,反映的是电子受激跃迁的程度,峰值代表光子能量。相变前,0 GPa时β-MgMoO4的光子能量为4.852 eV,1 GPa时β-MgMoO4的光子能量为4.869 eV;压致相变后,2 GPa时γ-MgMoO4的光子能量为6.525 eV,5 GPa时γ-MgMoO4的光子能量为6.705 eV。MgMoO4的光子能量随着压力的升高逐渐增大,相变后γ-MgMoO4光子能量得到快速提升。计算结果表明,介电函数的实部和虚部均随着压力的增加而增大,由此可以推断,MgMoO4的电通密度在压力的作用下会增加;材料的硬度也将随着压力的增加而增大,这与本文分析DOS得到的结论完全一致 [7] 。
3.3. 吸收光谱
吸收系数反映了材料对不同频率光子的吸收能力。图5为不同压力下MgMoO4的吸收谱,每一个压力点的图谱均可分为三部分,分别是0~15 eV、15~25 eV以及35~47 eV。
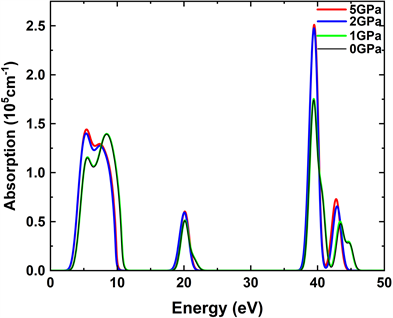
Figure 5. Absorption spectra of β-MgMoO4 at 0 GPa and 1 GPa and γ-MgMoO4 at 2 GPa and 5 GPa
图5. β-MgMoO4在0 GPa、1 GPa、γ-MgMoO4在2 GPa、5 GPa下的吸收系数图
0 GPa时,β-MgMoO4在能量为8.42 eV时,吸收光谱出现峰值1.39 × 105 cm−1,吸收光谱的能量范围是2.59~11.69 eV;在能量为20.13 eV时,吸收系数出现峰值0.51 × 105 cm−1,吸收光谱的能量范围是18.14~23.17 eV;在能量为39.40 eV时,吸收系数达到最大值1.74 × 105 cm−1,在能量为43.47 eV时,吸收系数出现峰值0.48 × 105 cm−1,吸收光谱的能量范围是37.23~46.57 eV。吸收边缘起始于2.59 eV的光能量处,对应于价带顶到导带底的电子直接跃迁阈值。
1 GPa时,β-MgMoO4在能量为8.42 eV时,吸收光谱出现峰值1.40 × 105 cm−1,吸收光谱的能量范围是2.60~11.77 eV;在能量为20.15 eV时,吸收系数出现峰值0.51 × 105 cm−1,吸收光谱的能量范围是18.15~23.25 eV;在能量为39.42 eV时,吸收系数达到最大值1.75 × 105 cm−1,在能量为43.38 eV时,吸收系数出现峰值0.50 × 105 cm−1,吸收光谱的能量范围是37.25~46.49 eV。吸收边缘起始于2.59 eV的光能量处,对应于价带顶到导带底的电子直接跃迁阈值。
相变后,2 GPa时,γ-MgMoO4在能量为5.34 eV时,吸收系数出现第一个峰值1.40 × 105 cm−1,吸收光谱的能量范围是2.22~10.68 eV;在能量为20.06 eV时,吸收系数出现第二个峰值0.59 × 105 cm−1,吸收光谱的能量范围是17.71~22.26 eV;在能量为39.46 eV时,吸收系数达到最大值2.47 × 105 cm−1,在能量为42.92 eV时,吸收系数出现峰值0.66 × 105 cm−1,吸收光谱的能量范围是36.98~44.99 eV。吸收边缘起始于2.22 eV的光能量处,同样对应于价带顶到导带底的电子直接跃迁阈值。
5 GPa时,γ-MgMoO4在能量为5.41 eV时,吸收光谱出现峰值1.44 × 105 cm−1,吸收光谱的能量范围是2.22~10.82 eV;在能量为20.13 eV时,吸收系数出现峰值0.60 × 105 cm−1,吸收光谱的能量范围是17.72~22.37 eV;在能量为39.50 eV时,吸收系数达到最大值2.51 × 105 cm−1,在能量为42.77 eV时,吸收系数出现峰值0.73 × 105 cm−1,吸收光谱的能量范围是36.99~44.87 eV。吸收边缘起始于2.22 eV的光能量处,对应于价带顶到导带底的电子直接跃迁阈值。
相变后的γ-MgMoO4相比于相变前的β-MgMoO4,随着压力的增大,吸收谱图在高能区发生了明显变化,43 eV附近的吸收峰随压力的增加向低能方向(43.47→43.38→42.92→42.77 eV),即长波方向移动,产生红移的现象。高能区的吸收系数随着压力的增加而增大,相变后的最大吸收系数大幅增加。β-MgMoO4的吸收系数由0 GPa下的1.74 × 105 cm−1增大到1 GPa下的1.75 × 105 cm−1,γ-MgMoO4的吸收系数由2 GPa下的2.47 × 105 cm−1增大到5 GPa下的2.51 × 105 cm−1。MgMoO4吸收光谱主要在3.5~7.3 eV、37~45 eV内,为紫外吸收,有较高的吸收系数,且可以通过压力进行调节。因此,我们认为这种材料在电子和光电子器件、紫外发光方面具有潜在的应用价值。
3.4. 反射率
图6为不同压力下MgMoO4的反射率随光子能量变化的关系。从图中可以看出,相变前,在0 GPa、1 GPa的压力下,β-MgMoO4的静态反射率分别为0.0607、0.0612;压致相变后,在2 GPa、5 GPa的压力下,γ-MgMoO4的静态反射率分别为0.0799、0.0817。对比可见,压力作用下导致静态反射率出现了明显的增加。这意味着高压相变使MgMoO4体系在光子能量为0 eV时的透射减弱,对红外光的反射提升。
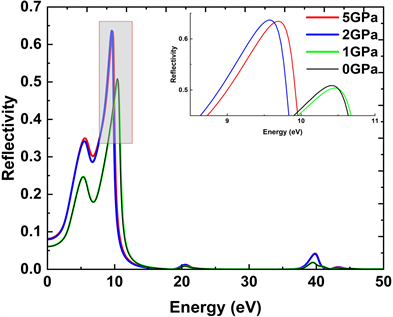
Figure 6. Reflectivity spectra of β-MgMoO4 at 0 GPa and 1 GPa and γ-MgMoO4 at 2 GPa and 5 GPa
图6. β-MgMoO4在0 GPa、1 GPa、γ-MgMoO4在2 GPa、5 GPa下的反射率谱图
在低能区,每一个反射谱在10 eV附近均展示出一个突出的峰。对于β-MgMoO4,随着压力0 GPa增加至1 GPa,该峰位从10.419 eV向高能方向移动到10.457 eV,对应的反射率从0.509减小到0.504。对于γ-MgMoO4,随着压力2 GPa增加至5 GPa,该峰位从9.557 eV向高能方向移动到9.697 eV,对应的反射率从0.637减小到0.635。
在0~14 eV内,MgMoO4以反射为主。反射光谱在低能区的范围基本上包含了可见光(1.57~3.18 eV)及以下的红外区域和紫外光(3.18~14 eV)的区域。对比不同压力下的反射光谱,压致相变后的反射峰强度明显增加,这意味着压力可以增大MgMoO4对可见、红外和紫外光的反射率,据此可以推断出MgMoO4在高压下是一种具有很好前景的涂层材料。
4. 结论
本文采用第一性原理,计算了不同压力下MgMoO4的晶体结构和光学性质,包括复介电函数、光吸收谱以及反射率,得出以下结论:1) 压致相变导致能带带隙减小的同时,也伴随着从直接带隙到间接带隙的转变。2) γ-MgMoO4的屏蔽性、对电子的束缚能力和极化能力在压力作用下显著增强,这有利于电子空穴对的分离,意味着压力可有助于改善材料的光催化活性。3) 光吸收结果表明,该样品的吸收系数可以通过压力进行调节。4) 在7~14 eV,MgMoO4以反射为主,表明该样品也是一种很有前景的涂层材料。本文的理论研究成果将对实验人员为以MgMoO4为基础的发光器件优化、改性和应用提供了思路和理论参考。
基金项目
黑龙江省基本科研业务经费(1451MSYYB006, 1453YB010);黑龙江省自然科学基金(LH2021A021, LH2023A014);牡丹江师范学院国家级课题培育项目(GP2022003);大学生创新创业训练计划项目(202010233005)。