1. 引言
实验动物作为在医药、生物工程等研究领域不可或缺的实验载体,其饲养环境要求严格,必须通过大量的新风对室内受污染空气进行稀释,造成了实验动物房空调系统耗电量极高的问题 [1] 。蓄能空调通过提前蓄能的方式可以达到削峰填谷、减少运行费用的目的,但由于传统的蓄能空调通常基于典型负荷工况进行储能,无法根据实际天气情况和运行状态变化进行精准的控制,存在空调蓄能不足或过量的问题 [2] 。
基于数据挖掘的方法可以对建筑负荷与天气及人员活动规律等因素的关系进行挖掘,根据工况对负荷进行预测,实现对蓄能空调系统的精确控制,缓解用能紧张的状况并降低运行费用 [3] 。由于空调负荷受到天气和人员活动规律等复杂非线性因素影响,需要采用可以更好处理非线性关系的模型对建筑负荷进行预测,目前常见的负荷预测方法主要有支持向量机、神经网络和随机森林以及其他统计算法 [4] [5] [6] 。BP (Back Propagation) [7] 神经网络以其强大的非线性映射、自学习、泛化、容错能力得到的广泛应用,但随着BP神经网络模型应用的越来越频繁,其收敛时容易陷入局部最优解问题也暴露了出来。为了解决此类问题,Chen [8] 等采用多种参数优化方法的BP神经网络来预测能耗,对各种优化算法的特点进行了比较,通过自适应权重粒子群算法优化的神经网络被证明在预测能源消耗方面是最准确的。侯勇严 [9] 等用灰狼优化算法(GWO)对BP网络的初始权值和初始阈值进行优化,并对电网发电量进行预测,与传统BP和GA-BP算法相比,精度分别提高了0.63%和0.32%。
以上优化算法在很大程度上避免了BP神经网络陷入局部最优化,但由于其优化算法中粒子位置随机的生成,它们在预测准确度方面仍然不尽人意 [10] 。VMD [11] 算法是一种对复杂信号进行分解并提取局部特征的信号处理方法,其对非线性负荷信号的分解能力强。于军琪 [12] 等利用VMD算法分解负荷序列,分别采用LSSVM、XGBoost模型建立负荷的非线性、线性子序列模型,重构叠加各子序列预测结果得到预测结果,仿真实验结果表明了该模型的预测精度有所提升。
本文采用Circle混沌序列 [13] 对灰狼算法 [14] 的灰狼个体位置更新方式进行优化,并对BP神经网络模型神经元阈值和权值进行寻优,增加BP神经网络更新自身权值与阈值过程中跳出局部最优化的概率,使用VMD算法将CIGWO-BP模型残差分解为多个相对平稳的子序列,并通过DTA模型对子序列进行预测后重构,与CIGWO-BP模型预测结果构成最终预测值,进一步提升模型的泛化能力和鲁棒性,为实验动物房蓄冷空调系统提供更加精确的运行依据。
2. 研究思路及模型建立
2.1. 模型建立
2.1.1. BP神经网络模型
BP神经网络(如图1)是一种采用前向传播和基于梯度降低的反向传播结合的方式对输出结果和误差进行传播的神经网络,其含有输入层、隐含层、输出层三层结构 [15] 。输入层神经元与输入参数个数相同,隐含层神经元数量通过公式(1)计算。输出层神经元个数与输出参数数量相同,本文设置为1,层与层之间通过权值连接,神经元内部设置阈值,权值的数量根据公式(2)和公式(3)计算。
(1)
(2)
(3)
其中,m为隐含层神经元个数;e为输入层神经元个数;r为输出层神经元个数;l为输入层到隐含层权值个数;k为隐含层到输出层权值个数。
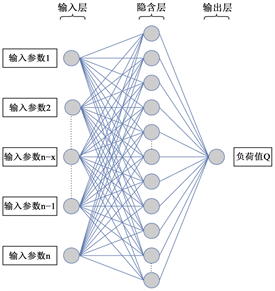
Figure 1. BP neural network topology drawing
图1. BP神经网络拓扑结构图
为了加快训练速度,对数据集进行归一化处理,统一量纲(如式(4))。
(4)
其中,
为初始数据集每一列的数据值;
为初始数据归一化后的数据值;
和
为每一列的最大值与最小值。
2.1.2. CIGWO-BP模型
通过引入Circle混沌序列对灰狼优化算法灰狼个体位置更新方式进行优化,再通过优化后的改进灰狼优化算法对BP神经网络模型的初始权值和神经元阈值进行迭代和优化,寻找到最优的权值和神经元阈值并代入到BP神经网络模型中,进而使用原始数据集进行负荷预测训练。CIGWO-BP模型实现过程如下:
确定对灰狼算法种群规模为N,最大迭代次数为
,寻优的空间维度D;
(5)
随机产生N个灰狼个体,并分别计算每个灰狼的适应度
,根据最小适应度选择对应的灰狼个体位置
。适应度计算方法如下:
(6)
(7)
(8)
其中,
为节点之间的权值;
为隐藏节点神经元的阈值的二进制编码形式;
为训练样本实际负荷值;
为预测值;
隐藏节点阈值及节点之间权值对应的灰狼个体位置更新计算方法如下:
(9)
(10)
其中,mod为取余函数,b = 0.2,a = 0.5,c为惯性权重;
更新灰狼个体位置;
评估灰狼个体适应度值并更新历史最优适应度值;
更新灰狼种群全局最优适应度值及对应的灰狼个体位置;
当
且未满足收敛条件时进行下一轮迭代,在达到收敛条件时或
且时迭代停止,输出最优权值和隐藏节点神经元的阈值;
将得到的最优的权值
和阈值
代入BP神经网络模型,完成CIGWO-BP模型的构造。
图2为CIGWO-BP模型预测实现流程图。
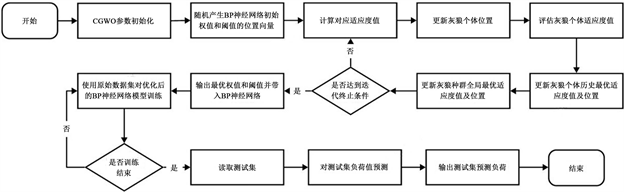
Figure 2. CIGWO-BP model prediction flow drawing
图2. CIGWO-BP模型预测流程图
2.1.3. VMD分解模型
由于空调负荷受到天气、建筑材料及人员活动等多因素影响,其具有明显的非线性。VMD采用非递归及变分模态求解模式处理原始信号,可以自适应的将CIGWO-BP模型预测负荷残差分解为具有特定稀疏性的模态信号,交替迭代的更新,寻找最优解,其分别代表预测负荷残差的不同特性。其算法如下:
将CIGWO-BP模型预测负荷残差
分解为不同带宽的分量
,中心频率为
;
使用希尔伯变换对分量
进行计算得到其频谱函数:
(11)
其中,
代表狄拉克函数;
代表卷积运算;
将CIGWO-BP模型预测负荷残差分量的频谱通过与指数协调的方式将
的中心频率转移到基带:
(12)
其中,
代表估计的中心频率;
通过高斯平滑原理,对
进行带宽解调:
(13)
其中,
为模态函数集合;
为模态的中心频率数据集;
将二次乘法因子
和拉格朗日算子
引入公式(13),将其从约束问题转化为无约束问题,公式为:
(14)
利用乘法算子交替方向法对式(14)解算,得到各分量
和相应的中心频率
:
(15)
(16)
其中,n为迭代次数;
、
、
代表
、
、
的傅里叶变换结果。
3. 仿真实验与结果分析
本文以苏州某实验动物房为例,获取2022年全年空调逐时负荷进行分析。此实验动物房净化空调区域面积281.6 m2,层高2.5 m。空调系统全天运行,制冷和制热工况下的室内温度分别设定为26℃和21℃,相对湿度分别设定60%和50%,净化空调换气次数设定为25次/h,空调区域外墙导热系数为0.6 W/(m2·k)。当室外环境温度处于22℃~24℃时不对新风进行制冷和制热处理。通过温湿度自计仪、太阳辐射观测仪和冷热量表对室内外温湿度、风、太阳辐射情况和空调负荷进行监测,采样间隔1 h,通过现PLC对数据进行数据存储(如图3)。

Figure 3. Laboratory animal room hour-by-hour load
图3. 实验动物房逐时负荷
3.1. 原始数据集构建
太阳辐射、风、大气压力、太阳高度、人员个数、室外温湿度、室内温湿度等对空调负荷值具有影响,并且由于空调负荷具有周期性 [16] 的特点,因此认为前一天同一时刻负荷值
对当前空调负荷具有参考意义。由于空调负荷不符合正态分布,本文使用SPSS分别对输入参数与当前空调负荷值进行斯皮尔曼秩相关性分析 [17] 。分析结果如表1所示,相关性系数绝对值超过0.2认为其相关性较强,其中人员数量的显著性水平超过了0.05,认为人员数量与实验动物房空调负荷没有显著性关系,由于24小时以后的太阳辐射强度获取难度较大,对室内相对湿度难以精确测量,因此将前一天相同时间的负荷值
、太阳高度、室外干球温度、室外相对湿度、室内干球温度作为负荷模型最终输入参数。

Table 1. Correlation coefficient of input parameters and loads
表1. 输入参数与负荷秩相关系数
3.2. CIGWO-BP模型参数设置
原始数据集共8736组数据,数据集采用5:1的比例对训练集及测试集进行划分。灰狼种群数量设置为50,阈值的上限
和下限
设置为1和−1,最大迭代次数设置为100。BP模型训练次数设置为1000,学习速率设置为0.01,训练目标误差设置为
,最小性能梯度设置为
。
3.3. 单一模型预测结果分析
通过原始数据集分别对BP神经网络模型、PSO-BP模型、GWO-BP模型、LIBSVM和CIGWO-BP模型进行训练及预测,并根据误差评定方法对其进行对比分析。由图4(a)可知,五种模型的预测结果均可以贴合实际负荷变化趋势,但其预测精度相差较大(见图4(b)),其预测精度CIGWO-BP模型最高,由高到底为CIGWO-BP模型、GWO-BP模型、PSO-BP模型、LIBSVM模型、BP模型,特别在波峰和波谷部分,对照组模型的误差相较于其他负荷值部分要更大,存在过估计的现象,总体预测负荷高于实际负荷,容易过度蓄能,造成能源浪费。通过BP模型、PSO-BP模型、GWO-BP模型与CIGWO-BP模型的预测精度的对比可以得出混沌映射理对灰狼算法的位置更新优化具有良好效果,可以使模型更好地跳出局部最优,预测精度较高。
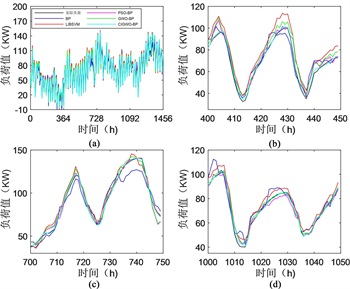
Figure 4. Graph of single model prediction results
图4. 单一模型预测结果图
3.4. VMD残差分解
空调预测负荷残差受到较多因素影响,具有较强的非线性、随机性和波动性,通过VMD可以分为将其分解为多个不同中心频率的相对平稳分量。在模态分量数量设置中,VMD模态分量分解数量过少会引起信息丢失,数量过多会引起模态混叠,造成信息的失真,影响预测精度。采用中心频率观察法确定分解的模态数量。不同模态分量个数K
对应的中心频率分布如表2。当分解变量个数为2时,IMF2的中心频率较低,表示欠分解,当分解变量个数为4和5时,IMF1和IMF2的中心频率较近,表示过度分解,模态之间出现混叠。
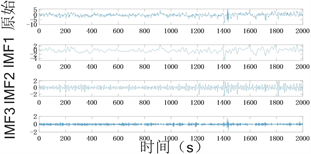
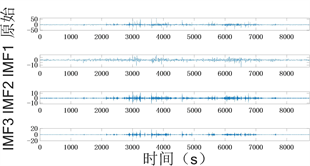
图5为K值为3时负荷残差模态信号的频谱图,从图中可以清楚的看出分解后的模态分量相互之间重叠较少,模态分量之间未出现模态混叠,可以将分解后的模态分量作为输出参数。
模态分量为3时,分解时域图如图6所示,图6(b)为截取的前2000个负荷残差的分解图,从图中可以清晰的看出三个模态分量代表不同信息,且与原始信号相比相对平稳。

Table 2. Center frequency corresponding to different K
表2. 不同K值对应的中心频率
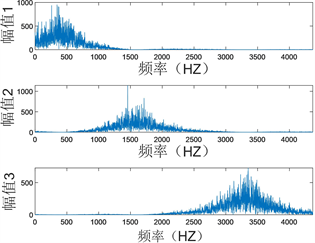
Figure 5. Graph of VMD frequency spectrum
图5. VMD频谱图
 (a) (b)
(a) (b)
Figure 6. VMD decomposition results
图6. VMD分解结果
3.5. CIGWO-BP残差分解优化模型建立
通过BP、决策树和LIBSVM模型分别对CIGWO-BP残差分解后的模态分量进行预测,将其预测结果与CIGWO-BP模型预测结果相加后而得到最终预测结果,并分别计算各个模型预测结果的MAE、MAPE和RMSE (如表3)。VMD-CIGWO-BP-DTA的MAE、MAPE和RMSE均为最小,因此后续使用决策树模型对单一模型残差的模态分量进行预测。

Table 3. Comparison of the residual decomposition optimization model performance
表3. 残差分解优化模型性能对比
如图7所示,VMD-CIGWO-BP-DTA模型的预测值与实际值的相对误差的绝对值在12%以下,其中相对误差较大的部分集中在实际负荷值接近0的时间段,此时相同的绝对误差比实际负荷值不接近0的时间段引起的相对误差会更大。另外,根据统计结果可知,相对误差在0%~2%的样本数量占全部数量的75.55%,相对误差在2%~6%的样本数量占全部数量的19.10%,相对误差在6%~10%的样本数量占全部数量的4.55%,相对误差在10%以上的样本数量只占全部数量的0.81%。通过上述模拟实验结果可以得出结论:VMD-CIGWO-BP-DTA模型对实验动物房空调负荷的预测中相对误差的波动随着实际负荷的变化波动较小,稳定性较强,可以较好的应对环境变化对预测效果的影响。
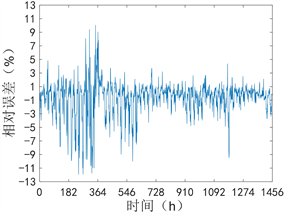
Figure 7. Relative error of VMD-CIGWO-BP-DTA model
图7. VMD-CIGWO-BP-DTA模型相对误差
3.6. VMD残差分解对单一模型性能提升
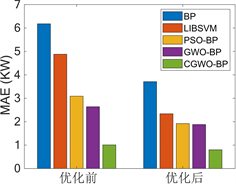
为进一步验证VMD残差分解对单一模型预测性能提升的有效性,采用VMD分别对BP模型、PSO-BP模型、GWO-BP模型、LIBSVM模型和CIGWO-BP模型的预测残差进行分解,并使用DTA模型对模态分量进行预测,与各单一模型预测值相加获得各自的最终预测结果。使用VMD残差分解后,以上5种模型预测结果的MAE降低幅度在20.79%到52.05%;MAPE降低幅度在27.72%到52.71%;RMSE降低幅度在22.45%到45.05% (图8)。由上述数据得出结论:对单一模型预测残差进行VMD分解并预测重构对模型预测性能会有较大提升。
4. 结论
为了实现对实验动物房蓄能空调负荷的精准预测,本文提出了一种基于残差分解的空调负荷预测模型,并进行了模拟实验分析。主要结论如下:
 (a)
(a)
 (b) (c)
(b) (c)
Figure 8. Comparison of model prediction performance
图8. 模型预测性能对比图
1) 通过Circle混沌序列优化的灰狼算法可以对BP神经网络预测模型的权值和阈值进行优化,相较于BP模型、PSO-BP模型、GWO-BP模型和CIGWO-BP模型有更好的预测精度,证明其可以更好地跳出局部最优。
2) 通过VMD对单一模型预测残差进行分解,可以得到相对平稳的模态分量,通过预测模型对分解的模态分量预测并将预测结果与单一模型预测结果相加可以较好地提升其预测精度。
3) 相较于BP和LIBSVM模型,决策树模型对VMD分解后的预测负荷残差分量进行预测并与CIGWO-BP预测结果相加得到的最终预测结果与实际值更加接近,建立的VMD-CIGWO-BP-DTA模型在对实验动物房空调负荷的预测中预测精度最高且效果稳定,具有较高的泛化能力和鲁棒性,可以为实验动物房空调系统提供更加精确的运行依据。
NOTES
*通讯作者。