1. 引言
在项目投资决策方法中,净现值法(NPV法)和内部收益率法(IRR法)考虑了整个项目周期内现金流的时间价值,为两种最常见的投资决策方法。在金融租赁公司实际应用中,一般只通过内部收益率法判断项目投资收益,本文从内部收益率法在金融租赁公司中的应用出发,分析内部收益率法的使用局限,并对内部收益率法进行修正,从而更科学地判断项目收益,指导金融租赁公司进行投资决策。
2. 内部收益率法在金融租赁公司中的应用
2.1. 净现值法与内部收益率法的含义
2.1.1. 净现值法(NPV)
净现值法:净现值是把项目在整个项目周期内的产生现金流按投资预期收益率换算为项目期初的资金净现值,净现值等于所有现金流入的现值与所有现金流出的现值的代数和。通过净现值与零的比较来判断该项目是否值得投资。
决策准则:按照项目投资预期收益率R折现,若NPV > 0,代表项目实际收益率超过预期收益率,项目值得投资;反之,若NPV < 0,则项目不值得投资。
NPV公式如下:
式中,Ct为t时间点现金净流量,R为投资预期收益率,N为项目周期。
2.1.2. 内部收益率法(IRR)
内部收益率法:内部收益率是资金流入现值总额与资金流出现值总额相等(即净现值等于零)时的折现率。通过内部收益率与项目投资预期收益率的比较来判断该项目是否值得投资。
决策准则:若IRR > R,代表项目内部收益率超过预期收益率,项目值得投资;反之,IRR < R,则项目不值得投资(R为项目投资预期收益率)。
IRR公式如下 [1] :
式中,Ct为t时间点现金净流量,N为项目周期,IRR为内部收益率。
2.2. 净现值法与内部收益率法的比较分析
2.2.1. 净现值法(NPV)
在净现值法的应用中,项目现金流的再投资收益率假设为项目投资预期收益率。净现值法考虑了现金流量发生的时间价值,计算较为容易,提供了一个与企业价值最大化目标相一致的客观决策标准。但是,净现值法无法直接反应投资项目可能达到的真实收益率,不够简洁直观;当项目投资额或计算期不同时,难以直接用净现值法判断多个项目之间的优劣;项目投资预期收益率确定比较困难,受主观因素的影响比较大。
2.2.2. 内部收益率法(IRR)
在内部收益率法的应用中,前提假设是项目未来产生的现金流能按照内部报酬率进行再投资。内部收益率法容易理解,简洁直观,易于比较;考虑了现金流量发生的时间价值,无需估计为了现金流的贴现率,受主观影响较小。但是内部收益率法计算较为复杂,未考虑项目投资与项目融资的不同,可能存在多个内部收益率 [2] [3] 。
2.2.3. 两者指标的比较
通过NPV和IRR的经济内涵的比较可知,NPV和IRR虽然都考虑了项目整个寿命的全部因素及资金的时间价值,但各有特点。
① IRR比NPV更容易理解,大多数情况下采用IRR作为项目投资决策的评价指标,因为一个项目带来15%的收益率回报比带来1万元NPV更容易理解。
② NPV计算比IRR简单,但必须给定基准收益率,并对项目的现金流的正负号是否改变没有要求。但基准收益率的制定对项目决策有重要影响,基准收益率定的太高,会把许多可行的项目排斥在外,定得太低会把不可行的项目当成可行项目,且基准收益率的测算需要消耗大量的人力、财力和时间。而IRR的计算比较复杂,需要试算求解,项目的现金流至少同时具有正负现金流量,在某些特殊现金流量情况下不存在正的IRR解或多个解或无解。
③ NPV是一个绝对值指标,直接反映了经济效益好坏,不同项目方案以相同折现率计算的NPV有可比性,多个项目方案进行决策时,相同折现率下NPV越大,方案越优。而IRR是一个相对值指标,不同项目方案的IRR无可比性,常使人误解;IRR越低的方案可能由于其规模较大,而具有较高的净现值,更值得建设;IRR越高的项目,未必就有更高的收益 [4] [5] [6] 。
2.3. 内部收益率法在金融租赁公司中的应用分析
金融租赁公司的租赁不同于一般企业的投资。企业一般进行的是单个项目的决策或多个项目的择优,用的是标准净现值法。而金融租赁公司资金不停高速流转,需要对不同时点、不同规模、不同租赁期的多项目进行决策,决策难度较大。且金融租赁公司涉及多个行业,若采用净现值法,基准收益率很难确定,因此一般选用内部收益率法作为指标 [7] [8] 。
金融租赁公司运用内部收益率法的另一个原因是IRR简单好算,用计算出的IRR与资金成本率进行比较,虽然IRR不是公司的利润率,但如果能保证每个租赁项目的IRR高于资金成本率一定值,公司的利润有保障 [9] 。
此外,在租赁项目初期,金融租赁项目的每期租金通过金融租赁合同的形式进行了法律确定,因此项目的资金流量在初期就可以准确预测,且每个单体项目的决策属于独立的投资项目决策,这也满足了内部收益率指标应用的前提条件 [10] 。
在传统的金融租赁过程中,金融租赁公司期初现金流流出,后续产生一系列现金流流入,此种情况下有且只有一个内部收益率,不存在多个内部收益率的情况。基于以上原因,金融租赁公司在进行项目投资决策时,多选用较为简洁直观的内部收益率法 [11] 。
3. 内部收益率法在金融租赁公司应用中的局限
3.1. 多个内部收益率的产生背景
金融租赁交易过程中,通常情况下出租人(金融租赁公司)采用现金放款的方式。在某些直租业务中,出租人与第三方供货人进行设备买卖,在供应链金融的背景下,该设备交易过程可以使用银行承兑汇票进行放款,供货人收到银票后可以选择向其上游供应商背书转让或贴现,出租人则可以通过银票延期付款来降低交易成本,从而降低承租人的融资成本。
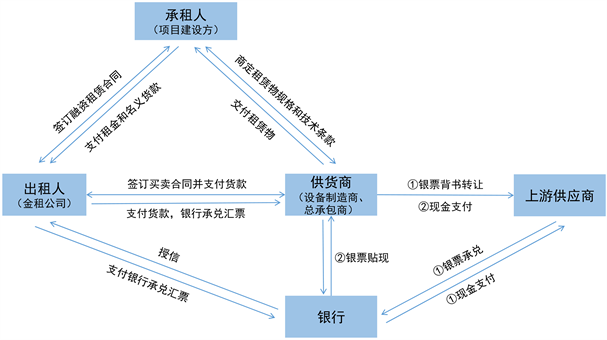
Figure 1. Direct leasing business process using bank note lending
图1. 使用银票放款的直租业务流程
使用银票放款的金融租赁业务流程如图1所示,在该情况下,金融租赁公司为银行承兑汇票出票人,通过银行承兑汇票向供货人购买租赁物,供货人为银行承兑汇票收款人,金融租赁公司作为出租人与承租人的现金流无变化。
方案A (单位:万元):

Table 1. Lease cash flow example using bank note lending
表1. 使用银票放款的租赁现金流示例
使用银票放款的金融租赁业务现金流示例见表1,利用Excel计算该情况的IRR时,将会产生多解,19.80%、4281.41%,无法进行准确判断。这种IRR多解多发生于未来现金流有正有负的情况,因为IRR求解本质上是解一元多次方程,会出现多个实数正解的情况。
3.2. 多个内部收益率的产生原因
传统金融租赁项目有一个初始投资,并且在其后产生正的现金流量,这样情况下内部收益率也只有一个。但当现金流量的符号发生多次变动时,根据笛卡尔符号规则,将可能出现多个内部收益率或无内部收益率 [12] [13] 。
笛卡尔符号规则:如果把一元实系数多项式按降幂方式排列,则多项式的正根的个数要么等于相邻的非零系数的符号的变化次数,要么比它小一个正偶数。而负根的个数则是把所有奇数次项的系数变号以后,所得到的多项式的符号的变化次数,或者比它小一个正偶数 [14] [15] 。
内部收益率方程式是一元高次(n)方程,若令(1 + IRR)−1 = x,零(CI-CO)t = at (CI为现金流入,CO为现金流出,t = 0, 1, 2, 3, …, n),则内部收益率方程可以改写为如下形式:
这是一个一元n次多项式,应该有n个解(其中包括复数根和重根),其中负数根无意义,只有正实数根才可能是项目的内部收益率,而方程的正实根可能不止一个。根据笛卡尔符号规则,n次方程的正实数根的个数不会超过项目净现金流量序列(多项式系数序列) a0,a1,a2,……,an的正负号变化次数p (如遇到系数为零,视为无符号)。
如果p = 0 (净现金流量序列正负号变化零次),则方程无根;
如果p = 1 (净现金流量序列正负号变化一次),则方程有唯一根;
如果p ≥ 2 (净现金流量序列正负号变化两次及以上),内部收益率方程可能有多解。
4. 内部收益率法的修正
修正假设
因采用银票方式投放时,银票的开票费相当于融资成本,因此在比较方案优劣时应加入融资现金流统筹比较总现金流(总现金流 = 投资现金流 + 融资现金流,以金融租赁公司的平均融资成本计算融资现金流,以4%为例)。通过相似的方案B的总现金流NPV逼近银票方案A的总现金流NPV,以方案B的IRR作为银票方案A的等效IRR。具体步骤如下:
① 计算银票方案A的总现金流NPV (以金融租赁公司的项目平均IRR作为NPV折现率,以7%为例);
② 计算相似的方案B (该方案只有一个IRR),相同的项目金额、手续费、期限、资金支付频率、成本计算方式等,改变租金利率使得该传统方案的总现金流等于上述银票方案A的总现金流NPV;
③ 以该方案B的IRR作为银票方案A的等效IRR。
上述案例计算等效IRR如下:
方案A (单位:万元):
以银票投放的金融租赁业务现金流量示例见表2,该方案NPV为602.8818万元。
方案B (单位:万元):
等效的方案B现金流量示例见表3,该方案利率为6.9967%,IRR为8.6137%,NPV为602.8818万元。该方案A的等效IRR为8.6137%,能较客观地反映该方案的IRR情况。

Table 2. Option A cash flow example
表2. 方案A现金流量示例

Table 3. Option B cash flow example
表3. 方案B现金流量示例
5. 结论
在传统金融租赁公司的项目评估中,使用内部报酬率法能准确反应项目投资收益的情况,但在现金流出现多次变号的情况下,内部报酬率法存在局限性,应对内部收益率法进行修正,使用等效IRR法可进行准确的项目投资决策。