1. 引言
随着中国特色社会主义进入新时代,中国生产力快速发展,使得中国社会主要矛盾已由“人民日益增长的物质文化需要同落后的社会生产之间的矛盾”转化为“人民日益增长的美好生活需要和不平衡不充分的发展之间的矛盾”。社会主要矛盾的转化标志着收入分配内涵也相应发生了转化,人民群众对收入分配也由数量要求向质量要求转变(张雷声,2022) [1] 。然而,近年来中国基尼系数仍超过0.4的国际警戒线,收入差距在全球处于中等偏高水平(唐任伍和许传通,2022) [2] ,这表明全体人民并没有平等共享中国经济高速增长带来的社会财富,有悖于我国实现共同富裕的根本目标。对于收入分配差距扩大问题,党和政府高度重视,出台一系列重要文件和规划部署。党的十八大坚持“初次分配和再分配都要兼顾效率和公平,再分配更加注重公平”,十九大报告强调“要坚持按劳分配原则,完善按要素分配的体制机制”,“十四五”规划纲要指出“坚持居民收入增长和经济增长基本同步、劳动报酬提高和劳动生产率提高基本同步”,二十大报告强调“坚持多劳多得,促进机会公平”、“增加低收入者收入,扩大中等收入群体”。2023年中央经济工作会议重点提到,要“增加城乡居民收入,扩大中等收入群体规模”。可见,国家一直高度重视收入分配水平的提升和收入分配格局的优化。持续推动收入分配公平,不仅能实现全体人民共同富裕的目标,还能积极扩大消费需求,进而高效拉动经济增长。因此,建设适应当下发展阶段的收入分配指标体系,深入研究中国各省市收入分配水平及地区间差异现状、演变态势、收敛特征等问题,不仅有助于把握中国现阶段收入分配现状,厘清收入分配失衡的内在原因,还能为切实解决收入分配失衡问题,制定优化国民收入分配格局的机制政策提供理据与参考。
收入分配是学界研究的热点问题,现有研究成果主要集中于三个方面。一是关于收入分配的理论研究,既有文献关于收入分配的内涵、影响因素及优化对策的探索较多。张俊山(2016)认为收入分配是国民经济活动的最终结果,它形成并影响着社会财富在社会成员中的分布和占有情况 [3] 。刘灿(2022)指出国民收入的初次分配指国民收入在物质生产领域内部进行的分配,再分配是在全社会范围内进行的国民收入在初次分配基础上的进一步分配,主要形式有财政支出、信贷、价格等,第三次分配是指人们完全出于自愿的捐赠和转移收入,比如对公益事业的捐献 [4] 。对于收入分配的影响因素,周克清、毛锐(2014)研究发现我国的税收制度整体上对收入分配呈现逆向调节作用 [5] ,张耀军、柴多多(2018)发现地区城镇化水平的提高有利于缩小该地城乡收入差距 [6] ,周国富、陈菡彬(2021)关注到产业结构升级对城乡收入差距的影响具有显著的双门槛效应 [7] 。在优化对策方面,贾康等(2018)建议把按劳分配与按其他要素分配相结合,同时主动施加调节以遏制收入分配“两级分化” [8] 。罗娟、彭伟辉(2022)强调应深化要素市场化改革、强化财政税收制度改革以及规范管理社会捐助与慈善事业,建立健全收入分配结构 [9] 。
二是关于收入分配状态的测度研究,主要包括对收入分配平等或不平等状态的衡量以及对收入分配差距的衡量。基尼(1987)根据洛伦兹曲线创建了基尼系数,用来衡量国家层面收入分配公平程度 [10] 。尚红云(2004)介绍了威廉森指数、泰尔指数、洛伦兹曲线法等11种方法,并通过这些方法度量收入分配不平等程度 [11] 。罗楚亮等(2021)运用洛伦兹曲线和基尼系数进行测算收入分配差距,结果显示中国居民收入分配差距长期持续处于高位震荡状态 [12] 。宿玉海等(2021)构建了基于恩格尔系数修正的效用指数模型,对中等收入群体进行测度,并据此将城镇家庭划分为低、中、高收入组 [13] 。万海远和王盈斐(2022)通过度量农村收入分配差距来反映收入分配状态,基于无条件分位数回归结果,发现观测期内我国农村内部收入差距呈现扩大趋势 [14] 。李实和陈基平(2023)使用资金流量表测度国民收入分配格局的变动趋势,并使用投入产出表分析行业间的收入分配状况,完整呈现国民收入分配格局的变化过程及其影响因素 [15] 。万相昱等(2024)以基尼系数作为不平等指标,分别使用回归树、随机森林、条件推断树和条件推断森林预测样本收入和测算收入机会不平等 [16] 。
三是关于收入分配水平评价指标体系的构建研究,学界普遍从收入分配公平与效率两个维度进行指标体系构建。吴振华(2015)重点研究初次收入分配水平评价指标体系,核心指标包括衡量绝对福利水平的人均劳动收入和衡量相对福利水平的劳动收入份额 [17] 。李宝瑜、刘雪晨(2016)采用基尼系数衡量收入分配公平,运用劳动生产率指标衡量收入分配效率,并以公平指标与效率指标之比构建了公平效率指数 [18] 。张巍、张奎(2019)构建了收入分配测度评价体系,包含体现效率和促进公平2个一级指标,分配效果、分配结果、分配活力、分配公平、分配差距、分配秩序6个二级指标及贫困发生率、劳动收入占初次分配比重等16项三级指标 [19] 。王阳等(2019)基于初次分配效率、初次分配公平和其他分配公平等3个评价维度,采用了劳动生产率、专利申请授权总量增长率及城乡居民人均可支配收入比等20项评价指标,构建了体现效率、促进公平的收入分配水平评价指标体系,并运用逐级等权法确定指标权重并计算具体数值,对收入分配工作做出分析与建议 [20] 。
上述研究成果为本文提供了理论支撑和经验借鉴,但仍存在研究空白有待进一步拓展和挖掘。一是现有文献主要集中于对高质量发展或收入分配的单向研究,即使有研究将两者结合,也大多是定性研究。此外,虽然学术界关于收入分配水平的评价指标的文献较多,但是基于高质量发展视角下的的收入分配水平指标体系几近空白。二是构建综合维度的收入分配指标体系并进行水平测度及地区差异分析的文章较少,且现有评价指标体系主要从公平、效率两个维度出发,尚不存在基于高质量发展的综合全面的收入分配水平指标体系。基于此,本文从上述方面进一步进行拓展:一是研究视角。基于现有的定性研究,本文从定量角度切入,构建了收入分配水平指标体系。二是研究内容。本文从经济发展效率、收入分配协调、绿色发展成果、收入分配共享四大维度构建了综合性收入分配水平指标体系。基于该指标体系,本文采用熵值法对中国31个省份2011~2020年间收入分配水平做出系统性评价,运用Dagum基尼系数测度收入分配水平的区域差异及其来源,并利用变异系数和收敛模型分析收入分配水平的空间收敛特征。
2. 研究设计
2.1. 收入分配水平评价指标体系构建与数据来源
为建设适应高质量发展的收入分配体系,本文参考了曾国安和胡晶晶(2013) [21] 、孙敬水和赵倩倩(2017) [22] 等学者以收入分配公平与效率视角进行的代表性指标分析和评价体系编制,结合“创新、协调、绿色、开放、共享”的新发展理念(马建堂和赵昌文,2020) [23] ,并在此基础上进行一定拓充,基于覆盖范围的全面性、评价维度的代表性和指标数据的可获得性,从经济发展效率、收入分配协调、绿色发展成果、收入分配共享4个维度、共计22个指标对不同省份的收入分配水平进行评价。其中,经济发展效率维度包含GDP、居民人均可支配收入、劳动生产率等7个指标,这些指标体现了地区的经济发展水平、居民收入状况,直接影响了国民初次收入分配。收入分配协调维度选取了与产业结构、城乡收入及消费结构、税收结构等相关的6个指标,它们是衡量收入分配是否公平的关键。绿色发展成果维度包括与资源消耗、污染治理、环境保护相关的5个指标,主要从两方面体现收入分配水平,一方面,环境治理的财政投入直接影响了国民收入再分配,另一方面,生态财富的私人占有问题和生态环境邻避问题仍然存在,与生态环境相关的生产要素被资本家投入生产并获取大量利润,但环境破坏的后果却由居民共同承担,这种负外部性破坏了收入分配的公平程度。收入分配共享维度选取了社会保障和就业支出占财政支出比重、医疗卫生支出占财政支出比重等4个指标,它们衡量了政府是否将更多的财政资金用于民生以改善二次收入分配。收入分配水平评价指标体系以及由熵值法计算后得到的指标权重如表1所示。本文测算2011~2020年中国31省市收入分配水平,所使用的研究数据主要来自2012~2021年《中国统计年鉴》、《中国环境统计年鉴》及各省市的统计年鉴、统计公报。

Table 1. Income distribution level evaluation index system and weights
表1. 收入分配水平评价指标体系及权重
2.2. 研究方法
2.2.1. 熵值法
熵值法通过计算指标的信息熵,根据指标的相对变化程度对系统整体的影响,即根据各个指标标志值的差异程度来确定各个指标的权重,相对变化程度大的指标具有较大的权重。熵值法是一种客观赋权法,它避免了人为因素带来的主观性偏差,具有较强的可信度和精确度,在统计学等各个领域被广泛应用。具体步骤如下:
1) 对评价体系中的指标数据进行标准化处理。设共有n个省市,m个评价指标。式中:xij代表第i个省市第j个指标的原始数据,Xij为xij标准化处理后的值。
正向指标:
(1)
负向指标:
(2)
2) 计算第i个省市占第j项指标的比重。
(3)
3) 计算第j项指标的熵值。
(4)
4) 计算第j项指标的权重。
(5)
5) 计算各省市的收入分配水平综合评价指数。
(6)
2.2.2. Dagum基尼系数分解模型
相比于传统的基尼系数和泰尔指数而言,Dagum基尼系数能够将样本的总体差异分解为组内差异、组间净差异以及组间超变密度,克服了子样本间的交叉重叠问题(Dagum C., 1997) [24] 。本文在分析中国31省市收入分配水平的地区差异时采用Dagum基尼系数分解模型这一方法,公式如下:
(7)
式中,G代表基尼系数,k代表划分的区域数量,n代表省份数量,nj(nh)代表第j(h)区域内的省份个数,Eji(Ehr)表示j(h)区域内i(r)省份的收入分配水平,
代表31省份收入分配水平的算术平均值。
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
分解Dagum基尼系数时,必须先对地区内各省份的收入分配水平均值进行排序,如式(2)所示。然后将总体基尼系数分解为区域内差异贡献(Gw)、区域间差异贡献(Gnb)和超变密度贡献(Gt),如式(3)所示。其中,Gjj表示区域j的基尼系数,Gjh表示区域j与区域h间的基尼系数,Djh表示区域j与区域h间收入分配水平的相对影响,将1 − Djh定义为超变密度。
(16)
(17)
djh表示区域j与区域h之间收入分配水平的差值,也可以理解为这两个区域中所有
的样本值加总的数学期望。同理,pjh代表区域j和区域h中所有
的样本值加总的数学期望。Fj(Fh)表示区域j(h)收入分配水平的累积分布函数。
2.2.3. 收敛模型
为了探究中国收入分配水平地区差异的演变态势,本文选取σ收敛和β收敛两种检验方法对其进行收敛性分析。二者的主要区别在于σ收敛是对存量水平的描述,而β收敛针对增量水平。
1) σ收敛。σ收敛表示不同区域收入分配水平的离差随时间推移呈不断下降的趋势。常用测度方法包括标准差(潘文卿,2010) [25] 、泰尔指数(刘亦文等,2016) [26] 、变异系数(梁红艳,2018) [27] 等反映离散程度的统计性指标。本文采用变异系数法进行考量,如果变异系数随时间推移越来越小,则认为收入分配水平存在σ收敛。具体公式如下:
(18)
其中,j表示中国东、中、西部区域,i表示区域内各省份,
为第j个区域省份的数量,
为第j个区域内部省份收入分配水平的均值。
2) β收敛。本文中β收敛是指随时间推移,收入分配水平相对落后的区域会因其更高的增幅而逐步赶上发达区域,二者差距逐渐缩小直至不同区域收入分配水平增长速度趋于一致(Barro R. J., 1992) [28] 。β收敛具体可分为绝对β收敛和条件β收敛。绝对β收敛是指在不考虑其他影响地区收入分配水平的因素的情况下,其发展趋势随着时间推移呈收敛状态。条件β收敛则是在考虑这些因素之后,各区域收入分配水平依然呈收敛状态直至各自的稳态水平。
由于相关面板数据可能存在空间依赖性,运用OLS模型进行回归可能会出现系数有偏或失效的问题,本文构建空间计量模型衡量 收敛。首先,使用LM模型检验空间自相关,若只有LM-lag检验显著选择空间滞后模型(SAR),只有LM-error检验显著选择空间误差模型(SEM),均不显著则选择经典空间回归模型(OLS);其次,构建Wald检验和LR检验判断空间杜宾模型(SDM)是否会退化为SAR模型、SEM模型;最后,采用Hausman检验选择固定效应模型或是随机效应模型。
(19)
(20)
(21)
(22)
式中,
是地区i在t + 1时期的收入分配水平
和在t时期的收入分配水平
的比值,代表该
地区在t~t + 1期收入分配水平评价指数的年增长率,α为常数项,ρ、λ、θ分别为空间回归系数、空间误差系数和空间外溢系数,
为空间权重矩阵,Z为控制变量,γ为控制变量的估计系数,φ为空间项的估计系数,
、
分别代表空间效应和时间效应,
是服从正态分布的随机扰动项。β为收敛系数,若β < 0且通过显著性检验,则说明收入分配水平初始指数与增长率呈负相关,存在β收敛;若β > 0且通过显著性检验,则呈现发散趋势。本文参考熊小林和李拓(2022)对收入分配影响因素的研究 [29] ,选取财政依存度、教育发展水平、交通发展水平、经济对外开放、国有化率作为控制变量。本文选用地方财政收入占生产总值的比重来衡量财政依存度(FD),在一定程度上它可以代表地区经济运行质量和财政调控力度,这是收入再分配的重要手段,可能影响地区收入分配水平。教育发展水平(ED)用人均受教育年限表示,它可以反映地区新增劳动力群体的受教育程度和人力资源开发水平。教育发展对收入分配水平的影响可能分为两方面,一是能够增加收入分配水平较低地区的人力资本,优化收入初次分配,二是可能进一步增大地区间的人力资本差距,使收入分配状况再度恶化。本文采用人均铁路营运里程和人均公路里程两个指标的加权和来衡量交通发展水平(TD),它通过影响地区运输效率和经济要素配置进而影响收入分配水平。经济对外开放(EO)用外贸依存度来表示,它是进出口总额与地区生产总值的比值,对外开放程度提升可以一定程度上增加贸易程度高的地区的居民收入。国有化程度(NR)用国有企业就业人数与地区总就业人数的比值来表示,它可能通过影响市场和效率进而对收入分配产生影响。
3. 中国收入分配水平测度、空间差异及其来源
3.1. 全国及三大区域收入分配水平时空演变特征
本文通过熵值法计算得到2011~2020年全国31省市的收入分配水平评价指数,为进一步呈现区域之间的差距,根据国家统计局对全国东、中、西部的划分1,对分属不同区域省市的评价指数进行均值处理,并绘制其收入分配水平演变趋势,结果如图1所示。由图1可以看出,全国及三大区域收入分配水平演变呈现如下特征。第一,在观测期内,东部区域收入分配水平评价指数均值显著高于全国层面及中、西部区域,全国评价指数均值位居第二,中部区域略低于全国平均水平,西部区域最后。其中,东、西部区域的收入分配水平评价指数均值差异明显,于2018年达到最大极差0.2375,这说明中国收入分配水平存在区域非均衡特征,以上分布结果可能与地区经济发展水平、财政拨款力度、政策调控范围相关。第二,全国及东、中区域的收入分配水平评价指数均值的变化趋势大体一致,自2011年起小范围浮动,在2014年明显上升,之后呈现“下降–上升–下降–上升–下降”的波动态势。西部区域评价指数均值的变化趋势较平稳,在2014年达到峰值,之后缓慢回落。第三,自2020年新冠肺炎疫情发生以来,除东部区域评价指数均值保持稳定,全国及中、西部区域都出现了明显下降的现象,这说明各区域收入分配水平均受到不同程度消极影响。政府需要继续坚持和完善收入分配制度,警惕和防范收入分配恶化。
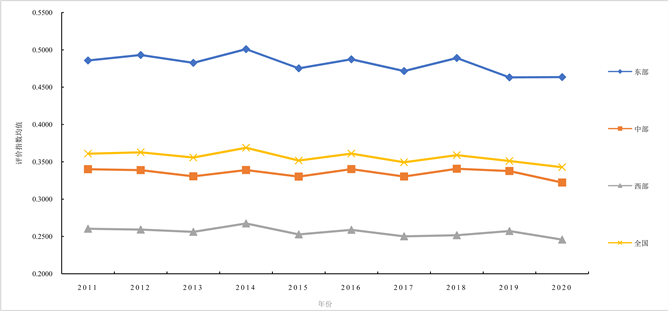
Figure 1. Evolution trend of income distribution level nationwide and in three major regions from 2011 to 2020
图1. 2011~2020年全国及三大区域收入分配水平演变趋势
3.2. 总体空间差异
本文采用Dagum基尼系数方法,测度了2011~2020年全国及三大区域收入分配水平总体差异的演变趋势,如图2所示。根据图2可以发现,观测期内中国收入分配水平存在总体空间差异,基尼系数值介于0.195~0.223之间,差异程度相对较低。演变趋势具体表现为:基尼系数在2011~2014年保持微弱上升趋势,2015年缓慢下降至0.2,2016~2018年出现反弹上升态势,于2018年达到极大值,到2019年又回落至0.212,之后到2020年又有所回升。总体而言,收入分配水平的总体差异大体呈现缓慢上升趋势,基尼系数由2011年的0.195增加至2020年的0.22,年均增长率为1.22%,增幅为12.85%。总体来看,中国收入分配水平的差距在不断扩大,原因可能在于某些地区劳动收入更高、资源配置更均衡、社会保障更完善,使当地收入分配向经济发展效率、收入分配协调、绿色发展成果、收入分配共享四个维度均衡发展,其收入分配水平进一步提升,而某些较落后的地区资源有限或者将重心放在经济建设上,无法充分平衡收入分配的效率性与协调性、绿色性、共享性,收入分配水平提升可能不明显甚至进一步恶化,最终呈现总体非均衡现象增强的态势。
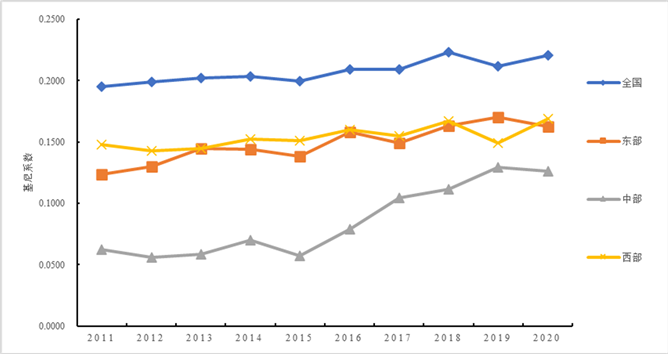
Figure 2. Overall differences and intra-regional differences in income distribution levels from 2011 to 2020
图2. 2011~2020年收入分配水平的总体差异及区域内差异
3.3. 区域内差异
图2还呈现了样本观测期内东中西部三大区域收入分配水平内部差异及其演变趋势。从数值差异来看,西部区域的区域内差异最大,基尼系数均值为0.154,其次是东部,均值为0.148,中部区域的区域内差异最小,均值为0.085。这说明西部区域内部收入分配水平的空间非均衡问题在三大区域中尤为突出,东部区域次之,中部区域的空间非均衡性最微弱,各省份收入分配水平差距较小。西部区域内部差距较为悬殊的原因可能在于,西部区域收入分配水平最高的省份是四川,全国排名第14,其次是重庆、内蒙古、广西、陕西,其余7个省份收入分配水平远低于上述省份,占据全国排名最后7位。从变化趋势看,东部区域整体处于上升趋势,基尼系数由2011年的0.123波动上升至2019年的0.17,最后下降到2020年的0.163,年均增长率为2.81%,增幅为31.92%。中部区域大致呈现向右上方倾斜的“W”形变化趋势,基尼系数由2011年的0.062下降至2012年的0.056,随后两年缓慢上升至0.07,于2015年明显回落至0.057,之后4年一路上升,直至2019年达到0.129,2020年略微下降到0.126。总体而言,中部区域基尼系数年均增长率为7.31%,增幅为102.48%,内部差异在波动中呈现明显扩大态势。西部区域总体呈现波动上升态势,虽然在2019年基尼系数经历了明显下降,相比2018年的0.167下降了0.018,但在2020年又回升至0.1691,总体来看,其基尼系数在观测期内年均增长率为1.34%,增幅为14.26%。以上结果分析表明,2011~2020年东中西部三大区域内部收入分配水平非均衡问题突出且省份间差异仍在扩大。值得注意的是,2020年东中部区域的基尼系数均开始下降,这提醒当地政府需要重视和把握区域内部收入分配水平差异缩小的势头,采取相应措施抑制各省份差异增大的趋势。西部区域内部差异呈现微弱扩张态势,可能与部分较落后省份的经济发展水平、国家政策支持等因素有关。
3.4. 区域间差异
图3体现了2011~2020年东中西部三大区域收入分配水平的区域间差异及演变趋势。从数值差异来看,东部与西部地区间基尼系数显著高于东部与中部、中部与西部,其均值为0.315;其次是东部与中部区域间差异,其基尼系数均值为0.205;中部与西部的区域间差距最小,其基尼系数均值为0.166。从变化趋势来看,东部与西部的区域间差异大体呈现“相对稳定–小幅上升–明显下降–微弱回升”的变化趋势,具体表现为:2011~2017年基尼系数波动幅度很小,极差仅为0.007,之后经历小幅上升过程,由2017年的0.314上升至2018年的0.332,在2019年又降至极小值0.3,随后在2020年微弱回升,达到0.319。总体来说,东部与西部区域间差异呈微弱上升趋势,基尼系数在观测期内的年均增长率为0.30%,增幅为3.06%。东部与中部的区域间差异主要经历了“稳步上升–微弱下降–平稳上升–小幅下降–反弹上升”的波动变化过程,基尼系数由2011年的0.195稳步上升至2014年的0.208,随后下降至2015年的0.199,在之后三年又上升至极大值0.215,然后在2019年略微下降到0.207,2020年回升至0.216。在观测期内,东部与中部地区间基尼系数年均增长率为1.07%,增幅为11.23%,这表明这两个地区收入分配水平的区域间差异仍在扩大。同样呈扩大态势的还有中部与西部的区域间差异,其主要变化趋势是“波动上升–微弱下降–小幅回升”,基尼系数由2011年的0.155上升至2018年的0.188,虽然在2019年有所回落,但对整体上升态势并未产生较大影响,2020年的基尼系数为0.184。在观测期内,中部与西部地区间基尼系数年均增长率为1.73%,增幅为18.71%。综合来看,中国收入分配水平区域间差异均呈现扩大趋势,具体原因可能是东部区域拥有较高的经济发展水平和良好的政府财政能力,能够显著提升居民收入分配质量,使得地区收入分配水平较高,而中西部区域尤其是西部区域因资源有限,对收入分配的拉动作用不明显,随着时间推移,各区域间的差距逐渐增大。

Figure 3. Inter-regional differences in income distribution levels from 2011 to 2020
图3. 2011~2020年收入分配水平的区域间差异
3.5. 区域差异来源及贡献
图4描述了2011~2020年收入分配水平的差异来源及贡献率。从差异来源的贡献率数值来看,观测期内区域间差异的贡献率远高于区域内差异和超变密度差异,区域间差异贡献率保持在64%~76%范围内,区域内差异贡献率居于第二,浮动范围在20.65%~25.03%之间,超变密度贡献率反应的是不同区域的交叉重叠部分对总体差异的影响程度,反映了区域间差异于区域内差异的交互影响,其数值最低,在4.22%~10.59%范围内浮动。三者的年均贡献率分别是70.85%、22.71%、6.44%,这表明地区间差异是我国收入分配水平总体差异的主要来源。从变化趋势来看,区域间差异的贡献率尽管在2015年和2020年有小幅回升现象,但对整体下降态势并未产生明显影响,由2011年的74.19%下降到2020年的66.84%,年均下降率为−1.04%,降幅为−9.91%。区域内差异总体变化幅度较小,其贡献率由2011年的20.9%上升至2020年的24.41%,年均增长率仅为1.56%,增幅为16.76%。超变密度贡献率整体呈现波动上升态势,其数值由2011年的4.9%上升至2020年的8.75%,虽然贡献率仍然较小,但增长幅度较大,年均增长率为5.96%,增幅为78.46%。总体而言,虽然区域间差异的贡献程度呈减弱趋势,但仍是全国收入分配水平总体差异的主要来源,因此,提升收入分配水平的均衡性,要重点关注区域间特别是东西部区域的差距。超变密度贡献率的提升表明并非所有东部区域省份的收入分配水平都优于中西部区域,虽然江苏、北京、广东等10个东部区域内部省份的收入分配水平评价指数均值位居全国前12名,领先优势明显,但同样属于东部区域的海南仍处于第24名,收入分配水平与其他省份有较大差距。因此在着力缩小区域间差距的同时,还应优化东部区域相对落后省份的收入分配格局。

Figure 4. Contribution rate of differences in income distribution levels from 2011 to 2020
图4. 2011~2020年收入分配水平的差异贡献率
4. 中国收入分配水平的空间收敛性分析
4.1. σ收敛
为揭示收入分配水平随时间推移的演变趋势,本文运用变异系数法分析2011~2020年全国及三大区域收入分配水平的σ收敛性,若变异系数随着时间推移呈下降趋势,表明各地区收入分配水平存在σ收敛特征;若变异系数随时间推移不断上升,说明各城市的收入分配水平差距扩大。如图5所示,就具体数值来看,全国层面的变异系数均值为0.381,高于东部区域的0.275、中部区域的0.162、西部区域的0.285,这表明全国范围内各省份的收入分配水平存在较为悬殊的差异,呈现两极分化特征,而中部区域内部省份的收入分配水平差异较小。就变化趋势看,全国层面的变异系数虽然在2014~2015年、2016~2017年、2018~2019年略微下降,但总体仍呈波动上升趋势,由2011年的0.355增长到2020年的0.404,年均增长率为1.3%,增幅为13.8%。相较全国,东部区域变异系数的波动幅度和上升趋势更为明显,由2011年的极小值0.235增加至2020年的0.299,年均增长率为2.44%,增幅为27.23%。西部区域变异系数的波动较为平缓,除2019年下降到0.28外,在观测期整体以上升为主,2020年的变异系数相较于2011年增加了0.04,年均增长率为1.37%,增幅为14.60%。中部区域大体呈现“波动上扬–明显下降–反弹上升”的变化过程,波动上扬的时间段主要在2011~2014年,这一阶段变异系数的变化幅度较小,在0.118左右浮动,变化趋势较稳定,之后在2015年出现了明显下降,由2014年的0.134降至2015年的0.111,自2016年起出现明显回升,一路增高至2020年的0.237。在观测期内中部区域变异系数年均增长率为7.22%,增幅为100.85%。总体而言,全国及三大区域变异系数随时间推移均呈现递增态势,这说明无论是全国整体还是东中西部三大区域,收入分配水平都不存在σ收敛,反而呈现明显的发散特征,地区间收入分配水平的绝对差距仍在不断扩大,不平衡问题更加突出。
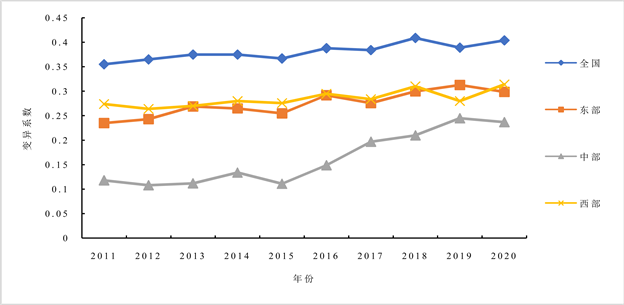
Figure 5. σ convergence evolution trend of income distribution levels across the country and three major regions from 2011 to 2020
图5. 2011~2020年全国及三大区域收入分配水平的σ收敛演变趋势
4.2. β收敛
4.2.1. 空间相关性检验
由于收入分配水平具有空间依赖和空间溢出,在进行β收敛检验前,需要采用Moran’s I指数测度其空间相关性,若存在空间相关性则建立空间计量模型,反之则建立普通面板模型。检验结果如表2,可以看出,在观测期内收入分配水平的Moran’s I指数值介于0.273~0.457之间,且都在1%的水平上通过显著性检验。这说明各地区的收入分配水平均存在显著的全局空间集聚效应,即收入分配水平高的省份有与收入分配水平较高的省份相邻的趋势,收入分配水平低的省份有与收入分配水平较低的省份相邻的趋势。随着时间推移,Moran’s I指数值由2011年的0.457逐步下降至2019年的0.273,在2020年又缓慢上升至0.325,总体呈现下降的趋势,说明收入分配水平的空间依赖性逐渐减弱。

Table 2. Moran’s I index of China's income distribution level from 2011 to 2020
表2. 2011~2020年中国收入分配水平的Moran’s I指数
4.2.2. 绝对β收敛
按模型选择步骤,全国层面使用了双固定SDM模型,东部区域使用了双固定SEM模型;中部区域和西部区域均使用了双固定OLS模型,前者是因为空间滞后模型ρ不显著,后者是因为空间误差模型λ不显著。由表3可得观测期内全国及三大区域收入分配水平的绝对β收敛检验结果。第一,从全国层面来看,空间系数ρ和空间项θ均在1%的水平下显著为正,说明全国收入分配水平存在显著的空间相关性,并且周边地区收入分配水平增长率的上升促进了本地收入分配水平提升。第二,从区域视角出发,全国以及东中西部区域的β系数均为负数且都通过了显著性水平检验,表明在考察期内全国及三大区域收入分配水平水平均存在绝对β收敛现象。如果各省份的财政依存度、教育发展水平、交通发展水平、经济对外开放和国有化程度相似,收入分配水平较低的地区会以较快的速度追赶,最终地区收入分配水平会随着时间推移逐渐收敛于某一稳态水平。第三,以收敛速度分析,全国收入分配水平的收敛速度最快,为4.78%,高于东中西部区域。三大区域中,东部区域的收敛速度最快、西部次之、中部最慢,其收敛速度分别为3.4%、3.29%和2.61%。这表明,随着时间推移,东部区域将率先实现收入分配水平的收敛,西部区域紧随其后,中部区域需要更长时间才能达到真实收入分配的稳态水平。东部区域最快收敛的原因可能是北京、江苏、广东等地区对周边省份具有较强的拉动作用,且辽宁、河北等省份一直积极推进工业结构调整,对收入分配水平有积极影响。西部区域收敛速度略低于东部但仍较快收敛,原因如下,一是西部区域收入分配水平省份差异较小且取值较低,根据新古典经济学关于收敛的理论,低水平地区通常拥有更快的增长速度;二是由于西部大开发战略持续推进,宁夏、贵州等欠发达地区的经济发展水平得到提升,带动其收入分配水平,区域协调发展程度显著提升。中部区域收敛速度最慢,这是由于中部各省份收入分配水平差距较大,评价指数均值最高的省份为河南,在全国位居第7,而均值靠后的山西、黑龙江、吉林则分别位于全国21、22、23名,且在观测期内追赶趋势不明显。
4.2.3. 条件β收敛
绝对β收敛是基于不同地区的财政依存度、教育发展水平等因素相似的前提下进行的检验,但实际上这些因素具有明显的差异性,所以有必要将它们作为控制变量进行收敛性检验,以提升实证结果的科

Table 3. Absolute beta convergence of income distribution levels across the country and three major regions
表3. 全国及三大区域收入分配水平的绝对β收敛
注:***、**、和*分别代表1%、5%和10%的显著性水平,下同。

Table 4. Conditional β convergence of income distribution levels across the country and three major regions
表4. 全国及三大区域收入分配水平的条件β收敛
学性和可借鉴性。在模型选择方面,西部区域选择了双向固定SDM模型;全国及东部区域按检验结果应选择双固定SDM模型,但由于空间回归系数ρ不显著,根据LM检验结果得出SAR统计量高于SEM,故均选择双固定SAR作为空间计量模型;由于SDM模型和SAR模型的ρ不显著,中部区域采用双固定OLS模型。表4报告了考察期内全国及三大区域收入分配水平的条件β收敛结果。第一,全国层面和三大区域收入分配水平的回归系数β均显著为负,说明在考虑了财政依存度、教育发展水平、交通发展水平、经济对外开放和国有化程度这些异质性影响因素的情况下,考察期内全国和东中西部区域均存在条件β收敛趋势。这表明全国各省份以及东中西部区域内各省份的收入分配水平随着时间推移能达到各自的稳态水平。第二,在收敛速度方面,全国收入分配水平的收敛速度为4.54%,东中西部三大区域的收敛速度依次为3.83%、2.72%、8.49%,其中西部地区的收敛速度最快,超过东部收敛速度的两倍,是中部收敛速度的三倍之多。第三,全国及三大区域各控制变量的回归系数和显著性水平存在差异。其中,财政依存度回归系数在全国层面及西部区域均为负数且通过了1%水平下的显著性检验,这说明当地财政依存度的增长抑制了收入分配水平的提升,原因可能是政府的财政收入增长速度过快,且财政收入的主要来源是较高的税收,同时增收部分没有合理地通过转移支付方式分配给地区低收入人群,再分配环节忽略了公平维度的落实,造成收入分配差距扩大。教育发展水平的回归系数在中部区域显著为负,说明中部区域教育发展水平提高未能有效促进收入分配水平的提升,可能是由于当地教育资源分配失衡,教育发展反而导致城乡人力资本水平差距扩大,或是教育水平提升反而加剧了中部区域的人才流失困境,这种消极效应超过为本地经济发展提供智力支撑的积极效应,进一步推动地区收入分配水平下降。交通发展水平的回归系数在全国和中部区域显著为负,说明提高交通发展水平不利于当地收入分配水平的提升,因为交通基础设施的建设可能进一步扩大城乡间的经济要素配置效率,损害了收入分配水平评价的协调维度。经济对外开放的回归系数在模型中都不显著,这说明经济对外开放对收入分配水平的影响暂不明确,其是否存在影响有待后续进一步探究。国有化程度的回归系数仅在西部区域显著为负,说明西部区域国有化率增加会阻碍收入分配水平提升,这是因为西部地区国有单位就业人员2020年平均工资水平为92,198元,私营单位就业人员2020年平均工资水平为50,491元,由于所有制不同而造成的收入差距损害了收入分配的效率和协调维度,对收入分配水平产生不利影响。
5. 研究结论与政策建议
本文根据2011~2020年中国31个省份数据,构建了收入分配水平综合评价指标体系,并运用熵值法对2011~2020年中国31个省份收入分配水平进行测度,采用Dagum基尼系数对全国和东中西三大区域收入分配水平的差异及其来源进行分解,随后采用变异系数法和收敛性模型对收入分配水平是否存在σ收敛、绝对β收敛和条件β收敛进行了实证检验。主要研究结论如下:
第一,各区域及省份间收入分配水平有明显差异。基于评价指数均值,可以看出东部区域收入分配水平最高,中部区域居中,西部区域最低。东、西部区域的收入分配水平评价指数均值差异明显,2018年达到最大极差0.2375,这说明中国收入分配水平存在区域非均衡特征。同时,不同省份收入分配水平也存在差距,江苏、北京、广东等省份收入分配水平遥遥领先,宁夏、甘肃、青海、西藏等省份收入分配水平有待提升。
第二,中国收入分配水平存在空间非均衡特征,总体差异的演变态势表现为波动上升,这说明全国层面的非均衡性持续增强。其中,西部区域的区域内差异最大,其次是东部区域,最后是中部区域。从区域间差距来看,东部与西部区域间基尼系数显著高于东部与中部、中部与西部,且它们的区域间差异均呈现上升趋势。从总体差异的来源来看,贡献率由大到小依次为区域间差异、区域内差异、超变密度。虽然区域间差异的贡献程度呈减弱趋势,但仍是全国收入分配水平总体差异的主要来源。
第三,收入分配水平的时空收敛性存在差异。其一,全国及东中西部三大区域收入分配水平均不存在显著的σ收敛特征。其二,全国及东中西三大区域收入分配水平存在显著的绝对β收敛趋势,在三大区域中,东部区域的收敛速度最快、西部次之、中部最慢。其三,在充分考虑了财政依存度、教育发展水平、交通发展水平、经济对外开放和国有化程度等异质性影响因素的情况下,全国及东中西部三大区域收入分配水平均存在显著的条件β收敛趋势,且收入分配水平较低的西部区域拥有较高的收敛速度,东部区域次之,中部区域最慢。
根据上述研究结论,全方位提升收入分配水平需要结合经济发展效率、收入分配协调、绿色发展成果、收入分配共享四个维度,从各省份实际情况出发,制定与之匹配的政策举措。为积极缩小地区间收入分配水平差距,减小其空间非均衡性,兼顾收入分配水平提升速度的协调性,优化收入分配格局,推动实现共同富裕,本文提出如下政策建议。
第一,完善收入分配机制,实行科学的收入分配政策。一是改善初次分配,提高劳动报酬的比重。坚持公有制经济为主体、坚持按劳分配为主体,持续完善劳动、资本、土地、知识、技术等各类生产要素由市场决定报酬的机制。二是注重建设再分配制度体系。持续降低中低收入群体税负,适当增强对高收入群体的税收调节力度,取缔非法收入,进一步提升税收调节收入分配功能。同时,将中低收入人群纳入公共服务和社会保障均等化的覆盖范围,促进社会公平。三是发挥三次分配的补充性作用。完善捐赠法、慈善法等法律制度及优惠扶持政策,积极推进慈善机构建设,大力培育慈善主体,引导社会组织参与分配环节。
第二,加强宏观调控,优化收入分配格局。一是持续强化就业优先政策。建立健全就业公共服务体系,扩大就业技能培训范围,着力提升居民增加收入的能力,在保障居民稳定工资收入的同时,使其实现长效增长。二是注重对低收入群体的有效帮扶。构建高质量的社会保障制度,注重加强基础性、普惠性和兜底性的民生建设。中央和地方政府应加大对农村、边远、民族地区等经济困难群体的财政支持力度,着力提升低收入群体子女受教育水平,健全养老保障制度,促进农村公共医疗卫生体系升级,使其向城镇基本公共服务标准靠拢,从协调、共享维度提高收入分配水平。
第三,深化区域协同合作,缩小地区间收入分配差距。一是根据西部地区产业发展需要,大力推进东中部与西部地区企业、科研院校之间的科技资源供需对接,既要加大科技创新投入、促进产业结构均衡,又要充分发挥西部地区地域优势,促进特色产业繁荣,保障居民收入协调增长。二是持续深化东中部地区与西部地区的劳务协作,定期组织开展职业技能培训,推动人力队伍的现代化建设,帮助落后省份提高劳动报酬。三是精准实施生态补偿机制,实现生态补偿多元化、市场化、协同化,增加对西部区域的生态补偿力度,这种横向转移支付能够显著提高受偿地区的农村和城镇居民工资性收入,使城乡居民的收入水平差距得到进一步改善。四是完善“三次分配”的对接协调机制,借助东中部区域社会慈善公益事业的支持,缓解贫富差距,助推西部区域收入分配水平提升,迈向共同富裕。
基金项目
2021年度重庆市社会科学规划基金项目“基于高质量发展的收入分配制度构建研究”(2021YBCS54)。
NOTES
*通讯作者。
1国家统计局将全国划分为东、中、西三大区域。东部地区包括北京、天津、河北、辽宁、上海、江苏、浙江、福建、山东、广东和海南11个省(市);中部地区包含山西、吉林、黑龙江、安徽、江西、河南、湖北、湖南8个省份;西部地区包括四川、重庆、贵州、云南、西藏、陕西、甘肃、青海、宁夏、新疆、广西、内蒙古12个省(市)。