1. 引言
石墨烯是一个具有蜂窝状晶格的单层二维碳原子阵列。石墨烯薄膜的成功制备已经引起了人们的广泛关注,这使人们能够直接探索二维Dirac-Weyl费米子 [1] [2] 的物理特性。在没有掺杂的情况下,石墨烯的带结构(能量色散关系)是由两个不等价的锥体(K, K’)组成,其位于布里渊区顶角,我们称之为狄拉克锥。在狄拉克锥点K(K’)附近的布里渊区,宽的单层石墨烯中的载流子表现出相对论性手性无质量粒子,
,其中
分别对应狄拉克锥点K(K’),其费米速度
,
是石墨烯面内电子的动量算符,
是泡利算符 [1] [2] 。与二维电子气体表现出的特性相比,这样的准粒子的存在引起一些不寻常的电子性质,如所谓的克莱因佯谬,异常整数量子霍尔效应,和观察最小电导率 [2] 。这些特性可能对石墨烯基器件的设计产生重要的影响。
石墨烯具有许多重要的应用性质,如门电压控制的载流子导电,高场效应迁移率和小的自旋轨道相互作用。它对未来的技术,特别是自旋电子学,是非常有前途的。基于此,一些关于石墨烯自旋电子学的研究已经开始实施。自旋注入到石墨烯薄膜已经成功地证明了非局域磁阻效应。此外实验上发现通过施加磁场,塞曼劈裂诱导石墨烯中载子出现自旋极化的特征,并在垂直电流方向产生自旋流 [3] 。此外,石墨烯可以通过掺杂和缺陷来产生磁性,也可以通过施加外部横向电场来产生磁性 [4] [5] 。已有理论预测 [6] [7] 和实验实现 [8] [9] ,石墨烯中可以通过铁磁邻近效应诱导诱导出有效分裂场Hex,通过调节Hex可以实现对电子自旋的调制,从而实现自旋滤波、自旋旋转的开关的设计。如由铁磁绝缘体EuO引起的石墨烯交换场的粗略估计为5 meV [7] 。最近的研究发现双层石墨烯与范德华反铁磁体CrSBr的界面有效劈裂能可在27~32 meV调制 [8] ,在石墨烯和铁磁氧化物绝缘层Tm3Fe5O12之间,自旋劈裂能在零磁场时可高达132 meV [9] 。
实验和理论研究电子自旋输运的一个常见手段是利用铁磁异质结来控制自旋极化 [10] [11] [12] ,获得极化电流。在实际应用中,常采栅极电压或是磁场进行调制。近年来,基于能带工程的进展,石墨烯费米速度的可控制性已经取得了很大的进展。实验上,石墨烯中的费米速度可以通过如掺杂 [13] 、衬底 [14] 、应变 [15] [16] 、电场进行调制 [17] 。此外,利用接地金属平板,考虑电子–电子之间的相互作用,通过重整化技术也获得费米速度可变的狄拉克点 [18] 。这些技术为调控费米速度达到实现对电子的可控性成为可能。然而,就我们所知,通过调控费米速度研究石墨烯异质结自旋电子输运还有待探索。
在本文中,我们设想磁性绝缘体处于靠近石墨烯层时,近邻效应诱导出交换劈裂场。我们可设计出石墨烯正常/铁磁/正常(N/F/N)异质结,其正常石墨烯层的费米速度可以通过掺杂或是接地金属平板进行调制。我们的目的是探索费米速度调制的自旋依赖输运的一种可能性。研究结果表明:不同自旋的电子透射系数和传导系数明显依赖于费米速度,呈现出近似周期振荡特征,自旋极化率可高达约−60%。
2. 理论推导
在本文中,我们构建石墨烯N/F/N异质结,并调控正常石墨烯层的费米速度研究其电子输运性质,如图1所示。描述具有可调制费米速度
的石墨烯N/F/N异质结准粒子的有效狄拉克方程由下式给出:
(1)
其中,其中
分别对应狄拉克锥点K(K'),Δ是铁磁绝缘体临近石墨烯产生的交换场,
分别对应代表电子自旋平行(
)和反平行(
)于交换场。在使用狄拉克方程时,我们假设速度变化在晶格常数尺
度上是缓慢的。在这个极限中,谷自由度并不会破除。注意到方程(1)中微分是作用于
,我们可以引入新的旋量函数
,则方程(1)变换为 [18] :
(2)

Figure 1. Diagram of the graphene N/F/N heterostructure where the Fermi velocity of electrons in the NG layer is modulated to be greater than, equal to, or less than the Fermi velocity electrons in the FG layer
图1. 石墨烯N/F/N异质结构示意图,在NG层中石墨烯电子的费米速度被调制大于、等于或是小于FG层中石墨烯电子的费米速度
石墨烯N/F/N异质结中准粒子的费米速度
在不同区间的分布如下:
(3)
考虑到
,进一步假设散射不会混合K点和K’点周围的动量,这意味着狄拉克K点
和K’点附近的散射互不相关,彼此独立。因此文中我们仅仅考虑狄拉克K点的行为,狄拉克K’点的行
为可以类比给出。对于K点,因系统在y轴具有平移对称性,系统所满足的狄拉克方程
所允许的波函数的解满足:
。令
。为求解波函数的具体表达
形式,不同区域的波函数可以用入射波和反射波来表示,如下:
(4)
其中
,
,
,
,
。角度
在区域I、II和III的分别被定义为入射角度,见图(1)。系数r、a、b和t由x = 0和x = L处的正确边界条件决定。为了确保几率流密度
在边界面处守恒,即
,波函数在边界面处需要满足 [18] [19] :
(5)
在这些匹配条件下,我们可以得到透射系数的形式为:
(6)
其中
。
在线性输运体系和低温条件下,我们可以从著名的Landauer Buttiker公式中引入电导率G,其表达
式为:
,考虑到
,因此g = 2,意味着狄拉克点处是谷简并的。利用
,并考虑
的条件,则
(7)
其中
,e是电子电量,h是普朗克常数,
是系统的费米能级。
自旋极化率可以表达为 [20] :
(8)
3. 结果与讨论
在接下来的数值计算中,我们选择石墨烯异质结宽度L = 100 nm,费米速度比值
和2,体系费米能级选定在100 meV,铁磁体临近石墨烯层诱导的交换场Δ被选择为0~50 meV。

Figure 2. Schematic diagram of the transmission coefficient of electrons in the graphene N/F/F heterojunction with the incidence Angle
图2. 石墨烯N/F/N异质结电子的透射系数随入射角度
的变化关系示意图
图2中,我们探讨了石墨烯N/F/N异质结电子的透射系数随入射角度
的变化关系。很容易看出,不同的自旋电子在费米速度调制下其透射系数表现出不同的振荡行为。当电子在正入射(
或
)时,我们很容易发现
,即此时电子很容易穿过异质结,无论各结区存在费米速度差异还是交换场,这是典型的克莱因问题 [2] 。此外我们也可以清晰地看到
。
当交换场
时,自旋是简并的,
,此时对应于速度垒模型 [18] 。对于
的情况,类似于光从光密介质进入到光疏介质,存在一个临界全反射角度
,当入射角度
大于临界角度
时,电子无法透过异质结。当
时,从方程(6)可知:
,这是很自然的,相当于不存在势垒区。
时,类似于光从光疏介质进入到光密介质,所有的入射角度
都是允许的。为解释透射系数的振荡行为,异质结中电子发生共振时,即当
的条件满足,从方程(6)可知,
,且n为整数时,共振条件成立。我们研究发现共振发生的条件与
有关。当
时,发生共振的量子态n
满足
,
时对应共振量子态n满足
。
研究结果显示:交换场Δ的存在,明显引起了自旋简并解除,同时也对共振量化条件产生了较大的影响。图中可以看出自旋
的电子更容易被囚禁从而形成窄的传输带隙,这相当于电子穿过一个势垒,特别是
的情况。而自旋
的电子在穿过异质结时,相当于电子穿过一个势阱,这将会有更多的传输波模对电子传输有贡献。这也导致了不同自旋电子明显具有不同的传输特征。这对设计依赖于电子自旋的波导模提供了一个新的思路,特别是在
的条件下,这种依赖电子自旋的波导模更容易实现。
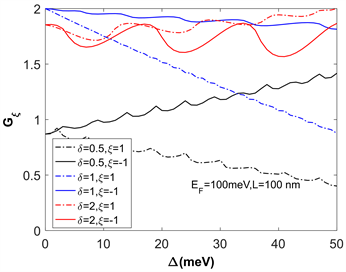
Figure 3. Schematic diagram of the electron conductivity of graphene N/F/N heterojunction with the exchange field Δ
图3. 石墨烯N/F/N异质结电子的传导系数随交换场Δ的变化关系示意图
图3中,我们研究了费米速度调制下的石墨烯N/F/N异质结电子的传导系数随交换场Δ的变化。图中我们可以明显看到依赖于电子自旋的传导系数呈现出近似周期振荡行为。这可能是交换场Δ的改变导致一些新的量化共振态的出现。自旋
对应的电子传导系数明显不同于自旋
对应的电子传导系数,这是不同传输波模和衰减波模共同作用的结果,这使得自旋
与自旋
的电子在传输过程中存在差异。因此基于此类异质结的自旋电子器件的研发与设计是可能的。图4中反映的是石墨烯N/F/N异质结电子的自旋极化率P随交换场Δ的变化关系,从中可以看到通过调节费米速度比值
和交换场Δ值,可以获得自旋极化率高达约−60%。
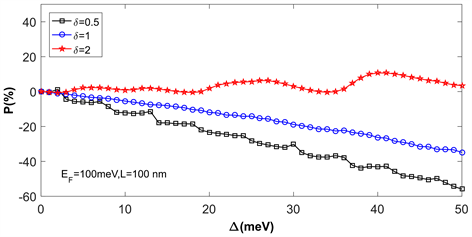
Figure 4. Schematic diagram of spin polarizability P of the electron in graphene N/F/N heterojunction with the change of exchange field Δ
图4. 石墨烯N/F/N异质结电子的自旋极化率P随交换场Δ的变化关系示意图
4. 总结
本文设计了基于空间费米速度调制下的石墨烯N/FN异质结,并研究了该模型中依赖于自旋的电子传输行为。实验上和理论上,通过掺杂、衬底、应变、电场进行调制,或是通过金属接触近邻效应,可以实现空间可调制的石墨烯异质结。近年来的理论和实验也发现通过不同铁磁体沉积于石墨烯层可以诱导出可观的交换分裂场。这些理论和实验上的研究对本文石墨烯异质结的设计提供重要的参考。交换劈裂场的出现,解除了石墨烯自旋简并。我们的研究结果发现不同自旋的电子透射系数和传导系数明显依赖于费米速度
和交换劈裂场Δ,呈现出近似周期振荡特性,自旋极化率可高达约−60%。这对于设计基于依赖自旋的石墨烯类电子器件提供了一定的指导价值。
基金项目
本文获得基金项目支持:国家自然科学基金(No. 11804063, 11447101),广西自然科学基金(No. 2016GXNSFBA380017),广西高校科研项目(No. KY2015LX046),大学生创新创业训练计划项目。