热力学中相对论性物理量的探讨与应用

Exploration and Application of Relativistic Physical Quantities in Thermodynamics

摘要: 狭义相对论的洛伦兹变换和质能方程是现代物理学的重要基本理论，其应用在物理学分支中具有普适性。热力学和相对论有着内在的联系，基本热力学参量在相对论时空观下有着与经典物理不同的形式。基于热力学中相对性温度的概念，建立了热质在一维导热情形下的相对论动质量与动能量、动量、压强的基本方程，引入了热子气等效质量，从而推导出其宏观运动的动能和势能表达式，并探讨了几个相对性热力学参量在现代物理中的应用。

Abstract: The Lorentz transformation and mass energy equation of special relativity are important basic theories in modern physics, and their applications have universality in many branches of physics. Thermodynamics and relativity have an inherent connection. The basic thermodynamic parameters have different forms from classical physics under the relativistic spacetime perspective. Based on the concept of relative temperature in thermodynamics, a basic equation for the relativistic kinetic mass, kinetic energy, momentum, and pressure of heat and mass in the case of one-dimensional thermal conductivity was established. The equivalent mass of hot gas was introduced, and the expressions for its macroscopic kinetic energy and potential energy were derived. The application of several relative thermodynamic parameters in modern physics was discussed.

1. 引言

爱因斯坦狭义相对论改变了人们对时空、长度、时间、质量、速度、引力等物理量的认识，为现代物理学的发展奠定了基础。在相对论建立起来后，通过探讨热力学与相对论之间的关联，建立了相对论热力学 [1] [2] 。1934年，托尔曼在个人著作《Relativity, thermodynamics and cosmology》中对于狭义相对论变换下平衡态热力学参量的变换行为就提出了具体的变换规则 [3] 。经典热力学研究方法在牛顿时空观和有限引力范围内是成立的。在相对论时空下，热力学研究对象的温度、压强、能量等参量都会发生变化，比如相对论热学中温度与坐标变换有关。在洛伦兹坐标变换或普朗克坐标变换形式下，质量膨胀效应会导致温度下降；而在奥特坐标变换下物体温度会升高。由此可见，热力学参量的测量结果与相对论有密切关系，经典热力学仅在牛顿力学框架下成立，但在相对论力学中可能不再准确。

对于相对论的热力学参量的推导和结论一直存在着争议，因此产生了不同的理论。就相对性温度而言，在坐标变化下有不同的观点。不同的相对论热力学理论下的观点又是相互交叉和联系的。目前，各种热力学参量的洛伦兹变换中熵是满足不变性的。本文我们将对一维热子气的相对性温度、相对性动质量、相对性动能量和相对性压强等热力学参量作详细讨论和对比，并探讨其在现代物理前沿的应用。

2. 相对性温度

相对论温度是热力学在相对论推广下的一个重要概念，普朗克和爱因斯坦提出热力学系统的相对性温度在洛伦兹变换下满足 $T_h=\frac{T}{\gamma }$ ，其中 $\gamma$ 相对论因子。在惯性系S₀中，设两个静止的相互接触的热力学系统A和B，假设初始状态B温度高于A。在热传递过程中，B向A传输一定量的热量 $\Delta Q$ ，达到热平衡状态的温度为T；在运动惯性系S中，平衡温度T_h和T的关系可由动量和能量公式导出。

两个热力学系统在S系中沿x方向以速度v运动，在洛伦兹变换下，动量和能量满足下列关系：

$P_x=\gamma \frac{v}{c^2}E,P_y=0,P_z=0$ (1)

$E_h=\gamma E$ (2)

则两系统的动量和能量的变化为

$\Delta E_{Ah}=\gamma \Delta E_A=\gamma \Delta Q=-\Delta E_{Bh}$ (3)

$\Delta P_{Ah}=\frac{v}{c^2}\gamma \Delta Q=-\Delta P_{Bh}$ (4)

设在x方向的力 $f_h=\frac{\text{d}P}{\text{d}t}$ ，在B向A传热的过程中动量做功

$\Delta W_A=f_h\Delta x=\frac{\Delta P_{Ah}}{\Delta t}\Delta x=\frac{\Delta x}{\Delta t}\Delta P_{Ah}=v\Delta P_{Ah}=\frac{v^2}{c^2}\gamma \Delta Q$ (5)

根据能量守恒及转换定律，系统A能量的增加，等于B向其传输能量与外力做功之和，即系统能量变化多了一项机械功

$\Delta Q_{Ah}=\Delta E_{Ah}-\Delta W_A=\gamma \Delta Q-\frac{v^2}{c^2}\Delta Q=\frac{1}{\gamma }\Delta Q$ (6)

对一个热力学微过程，可表示为

$\text{d}{Q}_{Ah}=\frac{1}{\gamma }\text{d}Q$ (7)

由熵在洛伦兹坐标变换下的不变性， $\text{d}{S}_{Ah}=\text{d}S$ 。结合热力学第二定律 $\text{d}Q=T\text{d}S$ 可得出平衡温度T_h和T的关系为

$T_h=\frac{1}{\gamma }T=\sqrt{1-v^2/c^2}T$ (8)

可见，在洛伦兹变换下，若保持热一、热二定律的形式不变，温度变换一定满足上式，系统运动物质的温度变低。此温度变换式的推导有多种，包括帕斯里亚、托尔曼等都用不同的方法推导出了温度在不同参考系中的变换关系是(8)式，但也有如奥特则认为托尔曼等在功的计算中引入了一个非理性力f，不应包含在加速功中。他认为对于给定的系统，在传热过程中做功可归结为静质量的增加，功和热量都应满足 $\text{d}{W}_h=\gamma \text{d}W,\text{d}{Q}_h=\gamma \text{d}Q$ ，在熵不变的情况下 $T_h=\gamma T$ ，给出了和托尔曼等完全不同的结论。随后，也有一些学者支持奥特推导的结论，如Mϕller、Bors等认为系统运动物质的温度升高。但在文献 [4] 中，谈镐生对奥特模型进行了修正并否定了上述结果，修正后的温度关系与爱因斯坦等推导的(8)式一致。

热力学系统的相对性温度和长度、质量等一样是洛伦兹收缩的，这是半个多世纪中，文献和教材普遍公认的协变结论。导致不同运动参照系中相对性温度的不同结论，实际上是与相对论本身无关的，因此到目前为止还没有一个被普遍采用的相对性热力学温度。王爱仁等 [5] 在普朗克和奥特两种相对性温度和热量的概念基础上，建立了一种自洽的相对论热力学理论。他们给与相对论温度一个补充定义，即温度为洛伦兹不变量，从而建构了有关运动参考系的温度不变量的热力学结构，并推导出相对应的相对性热量公式。关于热力学温度的相对论推广，还是与同时的相对性以及相对性原理是密切联系在一起的。因此，更多的物理学者认为温度收缩和温度不变的变换公式实际上并不存在本质的差异，而根本的要素是选取合适的相对性热力学量作为独立变量。

3. 相对性动质量

热质是基于狭义相对论中的质能方程提出来的。首先，回顾爱因斯坦狭义相对论的质能方程 $E=M{c}^2$ ，c是真空中的光速，M是粒子的相对性质量，E是粒子以远小于光速c运动的动能。热作为一种能量形式，可以当量等效为一定的质量，质能方程也适用。因此，无论对于传递的热量(过程量)或者热动形式的热能(状态量)都可定义热的相对性动质量 [6] ，也就是热质

$M_h=\frac{E}{c^2}$ (9)

即认为热质是热量对应的相对性动质量，静质量为零。值得注意的是，我们此处的热质和热力学史上提到的“热质说”中的“热质”是不同的概念，“热质说”将热量看作一种实体物质，温度升高或降低分别对应一定的热质的吸收或释放。热质会发生定向流动形成热流，因此也可以把热质看作一种流体，热流密度q满足傅里叶导热定律

$q=-k\frac{\text{d}T}{\text{d}x}$ (10)

热质的运动速度 $u_h=q/\rho CT$ ， $\rho ,C,T$ 分别为导热介质的密度、比热和温度。在稳态导热过程中，热质的运动速度与温度成反比，温度越低，热质运动速度就越快。这跟相对论质速关系是相似的，运动速度越大，质量膨胀越明显，温度反而降低。因此，由热质运动速度方程，我们可以推测出相对性动质量(热质)与温度的关系。基于质能关系，可得到热容密度 $q_V=\rho CT$ ，其热当量所对应的质量就是热质的密度 ${\rho }_h$ ，表达式为

${\rho }_h=\frac{q_V}{c^2}=\frac{\rho CT}{c^2}$ (11)

由(9)和(11)式可得，单位时间内热质运动的相对性动质量 $M_h={\rho }_h{u}_{h}S$ 。单位面积单位时间内热子气的等效质量为

${\stackrel{\dot{}}{m}}_h={\rho }_h{u}_h=\frac{\rho CT{u}_h}{c^2}=\frac{q}{c^2}$ (12)

可见，在通常温度T和密度ρ的条件下，热质的质量很小，且运动速度也远远小于光速，此时采用牛顿力学原理就可描述粒子的运动规律。例如，测量1 kg氮气在1000 K时所具有的热质大小，将热能除以光速的平方约为8.24 × 10⁻¹² kg，即使是最精密的电子仪器也很难测量出热质的大小，但热质已被实验证实是真实存在的。根据动质量的概念，当热子气物质的速度增加时，对应的能量也随之增加。从相对论观点出发，如果增加一个物体的速度，可以导致更大的能量产生，能量可以转化为质量，也就可能转化为其它静止质量更大的物质。

质能方程对于研究原子物理的研究有着重要意义，它解释了核聚变反应中的质量亏损和高能物理中的能量等问题。在实际医学实验中，我们所认识的正电子发射断层扫描就是应用的质能方程。在未来的科学研究中，质能方程会在新的现代物理理论中占有越来越重要的地位。对于高速运动的微观粒子而言，即使质量很小，但由于速度接近光速，仍然包含巨大的能量。但是，对于一个宏观物体来说，其运动速度是有限的，热量对应的相对论性动质量也非常小，几乎是可以忽略的，所以目前还未有相对论质能方程的研究应用于热学领域的相关报道。质能方程已应用于核能、能源转换和医学等领域，但如果热质和热动可以通过能量方程联系起来，其与最新科学成果的结合点会被找到，将会广泛应用于工程技术和现代物理的更多领域，揭示更多有关物质质量和能量的奥秘。

4. 相对性动能量

假设质量为M_h的热质被放置于温度为T的热场中，热质的存在将导致物质总质量和所包含的总能量增加，由于相对论性动质量而增加的能量定义为热质能。以一维稳态热子气运动为例，如图1所示。热质通过单位面积的总势能为

$E_{\text{p}h}=\frac{1}{2}\frac{\rho C^2{T}^2}{c^2}{u}_h=\frac{1}{2}{\rho }_h{u}_{h}CT=\frac{1}{2}{\stackrel{\dot{}}{m}}_{h}CT$ (13)

热质的宏观运动也致使其产生一定的动能，热质通过单位面积的总动能为

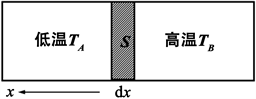
Figure 1. Schematic diagram of one-dimensional motion of heat and mass

图1. 热质的一维运动示意图

$E_{\text{k}h}=\frac{1}{2}\frac{\rho CT}{c^2}{u}_h^3=\frac{1}{2}{\rho }_h{u}_h{u}_h^2=\frac{1}{2}{\stackrel{\dot{}}{m}}_h{u}_h^2$ (14)

热子气动能取决于介质的物理性质(密度和比热)、热质的热流密度和温度。当温度T不太低、热流密度 ${\rho }_h$ 不太高时，热子气的动能相对势能可以忽略，此时的总能量 $E_h=E_{\text{p}h}$ ，(13)式可进一步化简为

$E_h=E_{\text{p}h}=\frac{1}{2}\frac{\rho C^2{T}^2}{c^2}{u}_h=\frac{1}{2}\frac{M_h}{c^2}{\left(CT\right)}^2$ (15)

可见，热质能 $E_h$ 是一种相对性动质能，上式与清华大学过增元教授 [7] 根据热电比拟方法提出的新物理量“火积” $G=MC{T}^2/2$ 的形式类似，仅相差一个系数 $C/c^2$ 。表明G的物理意义即物质的一种相对论性动质能(热质能)，间接说明热质和热质能在工程热物理学科的重要作用，对于复杂换热系统、能源利用效率等方面具有广泛的应用价值。在热质运动和传输的过程中，若考虑热质动能效应，那么温度梯度和热流密度之间并不呈理想的线性关系，此时傅里叶导热定律不再适用。过增元等基于热质运动方程对一维稳态导热和高热流密度情形给出了动能效应修正方程。

热质能转化和“火积”耗散存在着一定的联系，热传递过程中满足的能量方程形式是相同的。研究发现，自然界一切宏观的热传递过程，最终的结果都是导致火积耗散，这与热学中的熵增原理有着本质区别。山东大学许明田教授团队曾提出将火积理论取代熵来解释宏观意义上的热力学第二定律，但结果被梁新刚教授等否定。“火积”理论广泛应用于传热领域，例如换热器、相变传热、热传导与传输、热对流等方面。近几年，“火积”理论进一步被拓展应用于热力学循环分析领域和热泵系统，如清华大学梁新刚课题组基于相对性能量建立了热力学循环的火积平衡方程，并推导了与熵产最小化理论无关的新体系。随着火积理论的发展，热质能也将具有更多的应用优势。

5. 相对性压强

根据热质论，一定量的热质量可以等效为热量，热量的传递过程以固体中的电介质材料为例，根据德拜模型可以推导出热质满足文献 [8] 的状态方程，热子气压强P_h可表示为

$P_h=-\frac{\partial E}{\partial V}+\stackrel{\dot{}}{\gamma }\frac{\partial E_{D0}}{V}$ (16)

$\stackrel{\dot{}}{\gamma }$ 是材料的格律乃森(Grüneisen)常数，对于固体而言，上式第一项可忽略

$P_h=\stackrel{\dot{}}{\gamma }\frac{\partial E_{D0}}{V}=\stackrel{\dot{}}{\gamma }{\rho }_{h}CT$ (17)

对于室温下的Si而言，热子气的压强大约为5 × 10⁻³ Pa。对热质压强求导，可得到热质驱动力

$\frac{\partial P_h}{\partial x}=2\stackrel{\dot{}}{\gamma }\frac{\rho }{c^2}{C}^{2}T\frac{\partial T}{\partial x}$ (18)

在 $\rho ,C,T$ 不变时，热质驱动力与温度的梯度成正比，热质会在定向运动的x方向形成流动的热流。热流代表着一种“热惯性”的存在，Nernst曾预言低温下的热导体可能存在较大的热惯性而产生“热振荡”，Onsager也指出在热质导热过程中不应忽略热流加速(热惯性)所需要的时间。

以一维均匀导体中的导热过程为例，如图2所示。热流在流动过程中满足连续性方程

$\frac{\partial {\rho }_h}{\partial t}+\frac{\partial q_h}{\partial x}=0$ (19)

对于在体积元 $\text{d}V=S\text{d}x$ 中运动的一段热质的运动，由力学平衡可知，热质除了受驱动力 $\text{d}{F}_h$ 和介质内部的阻力 $\text{d}{F}_r$ 外，还要额外受加速过程中的热惯性力 $\text{d}{F}_i$ 作用，三种力的表达式如下：

$\text{d}{F}_h=\frac{\partial P_h}{\partial x}\text{d}V=2\stackrel{\dot{}}{\gamma }{\rho }_{h}C\frac{\partial T}{\partial x}\text{d}V$ (20-a)

$\text{d}{F}_r=-{\xi }_h{u}_h{\rho }_h\text{d}V$ (20-b)

$\text{d}{F}_i=\frac{D\left({\rho }_h{u}_h\right)}{Dt}\text{d}V=\left[\frac{\partial \left({\rho }_h{u}_h\right)}{\partial t}+u_h\frac{\partial \left({\rho }_h{u}_h\right)}{\partial x}\right]\text{d}V$ (20-c)

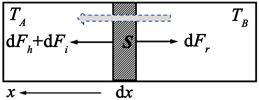
Figure 2. Schematic diagram of thermal conduction process in one-dimensional conductor (T_B > T_A)

图2. 热质在一维导体中导热过程示意图(T_B > T_A)

热流产生阻力采用粘滞力公式，粘滞系数为 ${\xi }_h$ 。热质运动的惯性力分为时间惯性(式(20-c)中第一项)和空间惯性(式(20-c)中第二项)。由牛顿第二定律可得到

$\text{d}{F}_h+\text{d}{F}_r+\text{d}{F}_i=0$ (21)

$2\stackrel{\dot{}}{\gamma }{\rho }_{h}C\frac{\partial T}{\partial x}-{\xi }_h{u}_h{\rho }_h+\frac{\partial \left({\rho }_h{u}_h\right)}{\partial t}+u_h\frac{\partial \left({\rho }_h{u}_h\right)}{\partial x}=0$ (22)

式(22)即热质相对性动量的守恒方程。在稳态导热条件下，时间惯性不存在，空间惯性导致介质材料的热导率与本征值相比有一定的偏离。如王海东团队 [9] 在温度为3 K低温环境、热流密度为1010 W/m²条件下，利用热质在厚为76 nm的Au纳米管中传播，观测到了热导率的偏离，证实了热质惯性作用的存在；熊世云课题组 [10] 在800~1000 K温度范围内，观测到Li₂S晶体中Li离子的跳动对热流热导率的影响，同样也观测到这种偏离现象。这为热质理论的正确性提供了直接实验证据。

热质的惯性作用的另外一个典型模型就是CV模型(热波传递)，仅考虑热流的时间惯性效应。2019年，麻省理工大学的研究人员在石墨材料中发现了“第二声”即热波现象 [11] 。他们在120 K实验温度下，发现当热质以接近音速的速度穿过石墨时，原本的热点会瞬间冷却。2022年，该团队实验发现石墨烯中的第二声可在超过200 K的温度下被观测到，这也是目前能观测到的第二声现象的最高温度 [12] 。在此之前，陈刚等 [13] 也曾通过实验证实石墨烯在一定温度范围内存在奇特的热波现象，热声子主要以相对论性动量守恒的方式相互作用。

6. 结论

1) 基本热力学参量与相对论有着密切的联系，在极高速运动时，传统热力学研究方法不再适用。在通常T和ρ的条件下，热质的相对性质量很小，流动速度远远小于光速，采用牛顿力学原理描述热质的运动规律。

2) 狭义相对论中的质能方程适用于热学的能量形式，热质在一维稳态运动下的热质能是一种相对性动质能，引入了等效质量，相对论性动能可表示成与经典相同的表达式，指明了等效质量的物理意义。

3) 电介质材料中热子气受驱动力作用形成热流，基于流体力学的三种力分析建立了热质的相对性动量守恒方程。热流代表着热惯性的存在，热质惯性力会间接导致热导率的偏离。

基金项目

安徽省高校优秀青年人才计划项目(gxyq2022018)；国家级大学生创新创业训练计划项目(202310361085)；芜湖市科技计划重点研发项目(2023yf030)。