1. 引言
1.1. 研究背景
在营养学领域,鸡蛋一直被誉为“全营养食品”,它所富含的多种营养成分,对人体生长发育、提高免疫力、促进新陈代谢以及保护视力具有不可或缺的作用。作为日常饮食中的核心食材,鸡蛋的价格呈现一定的波动性。这一波动性受到多种因素的影响,包括市场供需关系的变化、养殖成本的增减、天气状况以及季节性需求等,这些因素的综合作用导致鸡蛋价格呈现不断涨跌的现象,成为社会各界的关注焦点。据农业部监测数据显示,2000年至2015年中国鸡蛋价格出现了14次小周期波动、7次大周期波动;特别2007年以来,中国鸡蛋价格波动愈发频繁 [1] 。鸡蛋价格的波动不仅直接影响消费者的购买成本,还影响着养殖户的收益以及投资者的投资策略等。因此,分析鸡蛋价格的波动特征及其规律,并且及时、准确地对鸡蛋市场价格未来走势及供应进行研究显得尤为重要。
1.2. 研究现状
近年来学者们对鸡蛋价格的分析和预测进行了不同研究。武嘉平从成本、生产供给及市场需求3个层面对鸡蛋价格变化的原因进行了定性研究,并指出饲料价格变动是引起蛋价波动的主因 [2] 。李雪莹,武翔宇运用格兰杰因果检验、脉冲响应函数和方差分解对鸡蛋期货的影响因素进行实证分析 [3] 。汤路昀,祁春节运用空间模型对鸡蛋价格的空间相关性进行验证,得出中国鸡蛋价格集聚效应显著,且以“H-H”和“L-L”型集聚为主等相关结论 [4] 。刘诗博,李作臣等利用CensusX12季节调整法,分析出鸡蛋年内价格波动规律,主要是冬春季节波动小,夏秋季节波动大 [5] 。宋淑婷运用计量经济学方法将鸡蛋价格分解为长期趋势、周期波动、季节波动和随机波动四个方面,进而分析各方面的变化规律及形成原因 [6] 。王舒鸿先对波动较大的数据进行弱化,应用灰色波形预测,预测出未来鸡蛋价格上下限 [7] 。刘雪,刘锦涛等提出了基于时间序列季节性分解方法(STL)和长短期记忆网络(LSTM)组合的鸡蛋价格预测模型STL-LSTM [8] 。李哲敏,李干琼系统分析禽蛋市场价格的主要影响因素,筛选出4个能够及时、全面获取数据的相关因子作为自变量因子,对禽蛋短期市场价格进行因子预测模型的建立 [9] 。刘林静,楼文高将GRNN模型应用于鸡蛋价格的预测,并不断优化分组,最终确定所建模型的平滑因子为0.02 [10] 。
从现有文献来看,在鸡蛋价格的分析和预测方面既有基于经济理论角度的研究阐述,也有基于实际数据以及构建模型的研究。但是,以实际数据用时间序列分析方法解决鸡蛋价格预测的研究则相对较少。学者们应用的主要有LSTM模型、GRNN模型和灰色预测模型等,到目前为止,ARIMA模型以及残差自回归模型较少应用在国内鸡蛋价格预测领域上。除此之外,传统的鸡蛋价格分析和预测方法主要基于时间序列分析,如指数平滑、灰色预测等,还有基于机器学习方法,如LSTM模型等。然而,这些方法在处理非平稳时间序列时存在一定的局限性,即预测精度和解释性有待提高,而ARIMA模型和残差自回归法既考虑了季节效应和长期趋势效应还考虑了随机波动,大大提高了预测精度。因此为了寻找更为合适的预测模型和方法,本文在吸收前人研究成果和经验的基础上,以广东省2003年1月~2011年12月的鸡蛋价格为例,应用ARIMA模型和残差自回归法分别对鸡蛋价格进行分析和预测,并且对结果进行比较分析,探讨出最优的鸡蛋价格预测模型,并根据估计结果,提出稳定鸡蛋价格的意见建议。
2. 数据预处理
2.1. 数据概况
本文所采用的数据来源于中国经济社会大数据研究平台。由于在中国畜牧业年鉴中只有2003~2011年的数据,因此本文获取了2003年1月至2011年12月的广东省鸡蛋价格,这是一个包含108个观测值和2个指标的数据集,详见附录表A1。这个数据集详细记录了2003年1月至2011年12月广东省的鸡蛋价格,并以月度为单位进行了时间标记。通过这些数据,对鸡蛋价格的进行分析和预测,为进一步的研究和分析提供有力支撑。
2.2. 白噪音检验
在处理时间序列数据时,通常只对非白噪音数据感兴趣,因为白噪音数据缺乏分析和研究的价值。因此本文在分析之前首先对2003年1月至2011年12月广东省鸡蛋价格序列进行了白噪音检验。通过这一检验,我们可以判断该数据是否具有非白噪音特征,从而确定其是否具有进一步分析和研究的价值。
白噪音检验结果如表1,可以看到给定显著性水平为0.05下,该序列在滞后各阶下LB统计量的P值都小于显著性水平,所以拒绝序列为纯随机序列的原假设,认为广东省在2003年1月至2011年12月的鸡蛋价格序列为非白噪音序列,序列有相关信息仍未被提取出来,值得后续分析和研究。

Table 1. White noise test of egg price sequence in Guangdong Province
表1. 广东省鸡蛋价格序列白噪音检验
2.3. 平稳性检验
由于应用ARIMA模型和残差自回归模型的前提是时间序列非平稳,因此在构建模型之前,对序列进行平稳性检验时是必要的。首先对2003年1月至2011年12月的广东省鸡蛋价格数据绘制出时序图,由图1可以看出鸡蛋价格有明显的递增趋势,并且该序列可能有以12个月为周期的季节性,所以可以初步判断为非平稳序列。
用ADF检验对序列平稳性做出精准的判断,检验结果如表2,可以看到当最大滞后期数2时,在显著性水平为0.05下,不管是带有趋势项还是截距项的模型,对应的P值都大于0.05,因此检验结果都是不能拒绝原假设,认为该序列不平稳。因此,广东省在2003年1月至2011年12月的鸡蛋价格序列不平稳。

Figure 1. Time series of egg price in Guangdong Province from January 2003 to December 2011
图1. 广东省2003年1月~2011年12月鸡蛋价格时序图

Table 2. ADF unit root test results of egg price sequence in Guangdong Province
表2. 广东省鸡蛋价格序列的ADF单位根检验结果
3. ARIMA模型的构建
基于上述分析,广东省鸡蛋价格序列不平稳,构建ARIMA模型对鸡蛋价格进行分析。
3.1. 差分平稳化
首先对广东省鸡蛋价格序列进行一阶差分后进行ADF检验,判断差分后序列是否平稳。得出的结果显示当最大滞后期数2时,在显著性水平为0.05下,不管是带有趋势项还是截距项的模型,对应的P值都小于0.05,因此检验结果都是拒绝原假设,认为该序列平稳。为了消除季节性,还要对序列作12步差分,并绘制出最终时序图进行观察,如图2。观察绘制的时序图,可以发现经过一阶12步差分后,原序列的长期趋势、季节变动基本消失,序列基本在某一均值附近上下随机波动,序列平稳。根据ADF检验结果对广东省鸡蛋价格一阶12步差分序列的平稳性再次进行判断,可以得到所有模型都拒绝原假设的结果,即序列平稳。

Figure 2. Time sequence diagram of egg price in Guangdong Province after first order twelve-step difference
图2. 广东省鸡蛋价格一阶十二步差分后的时序图
最后对一阶12步差分后的序列进行白噪音检验,根据结果显示,差分后的序列在12期以后的P值小于显著性水平0.05,拒绝原假设,所以差分后的序列不是白噪音序列,需要模型继续拟合。
3.2. ARIMA模型定阶
广东省鸡蛋价格时间序列在经过一阶差分消除趋势和12步差分消除季节效应之后,序列变平稳。这为下一步的阶数确定打下了良好的基础。本文采用两种季节模型,根据差分后序列的自相关和偏自相关图确定对应模型的各个阶数。
对于简单季节模型,差分后的序列在延迟8阶和12阶自相关系数和偏自相关系数都在两倍标准差范围外,因此初步选用
模型进行拟合。
对于乘积季节模型,原序列经过一阶差分运算后,序列的趋势基本消除,所以
,经过12步季节性差分,季节性基本消除,所以
。序列的自相关系数图中只有8、12阶显著不为零,12阶以后基本截尾;偏自相关图中8、12、21阶显著不为零,而且到24阶还有反弹。综上所述,初步考虑采用模型
。
3.3. ARIMA模型参数估计及检验
对简单季节模型
的参数进行估计,并进行模型检验。可以发现部分参数没有通过检验,因此再次对模型进行调整,最终选择模型
对差分后的序列进行拟合。根据模型检验结果,在给定显著性水平0.05时,参数检验的P值都小于显著性水平,各个参数都通过了检验。同时各阶滞后下LB统计量的P值都大于显著性水平,所以不能拒绝序列为纯随机序列的原假设,即残差序列为白噪音,信息提取完全。
对乘积季节模型
进行参数估计,并进行模型检验。可以发现部分参数没有通过检验,因此再次对模型进行调整,最终选择模型
对差分后的序列进行拟合。根据模型检验结果,在给定显著性水平0.05时,参数检验的P值都小于显著性水平,各个参数都通过了检验。同时各阶滞后下LB统计量的P值都大于显著性水平,所以不能拒绝序列为纯随机序列的原假设,即残差序列为白噪音,信息提取完全。
3.4. ARIMA模型确定
上述两个模型都通过了模型检验,都能够将信息基本提取,但是通过对比两个模型得出的AIC值和SBC值,如表3,可知乘积季节模
更优一些。这也说明了该序列的季节效应、长期趋势效应和随机波动之间有着复杂的相互关联性,因此用简单的季节模型不能充分地提取其中的相关关系,拟合效果较差一些,而乘积季节模型可以很好的提取这种相关关系。

Table 3. Comparison of ARIMA models
表3. ARIMA模型对比
3.5. ARIMA模型优化
将参数估计结果与差分代入式子中,可以得到拟合广东省2003年至2011年鸡蛋价格发展的ARIMA乘积季节模型
为:
(1)
其中,B为延迟算子,
为广东省鸡蛋价格序列,
为残差序列。
3.6. ARIMA模型预测
根据所建立的
模型,对广东省2012年1月~12月的鸡蛋价格做出预测,预测结果如表4。将结果绘制出效果图如图3,其中黑线为真实观察值,红线为估计和预测值,绿线为估计值的上下限。根据效果图可以看出该模型拟合效果较好,基本所有的鸡蛋价格都落在置信区间内。

Table 4. ARIMA model egg price forecast in Guangdong Province from January to December 2012 (unit: Yuan)
表4. ARIMA模型广东省2012年1月~12月鸡蛋价格预测(单位:元)
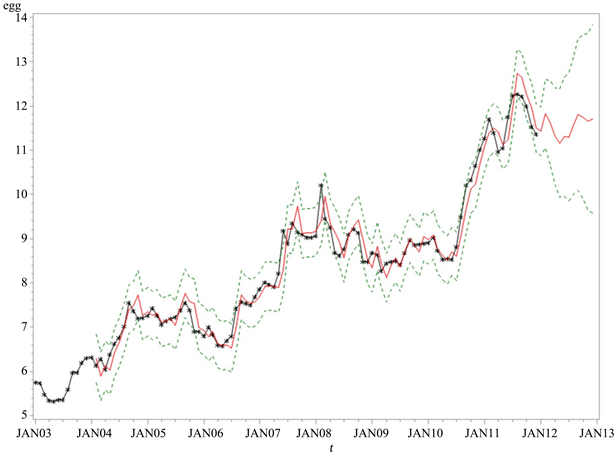
Figure 3. ARIMA model fitting and prediction renderings
图3. ARIMA模型拟合和预测效果图
4. 残差自回归模型的构建
基于上述分析,广东省鸡蛋价格序列不平稳,构建残差自回归模型对鸡蛋价格进行分析。首先通过确定性因素分解方法先提取广东省鸡蛋价格序列中主要的确定性信息,分为趋势效应和季节效应,接着对残差序列拟合自回归模型,以便更加充分提取序列信息,即
(2)
4.1. 拟合季节效应
本文利用季节指数对广东省鸡蛋价格序列的季节效应进行拟合。用季节指数方程可以计算出各个月份的季节指数,结果如表5。

Table 5. Seasonal index of egg price in Guangdong Province by month
表5. 广东省鸡蛋价格各个月份的季节指数
将原始鸡蛋价格数据除以对应月份的季节指数,目的是消除季节效应,相应的公式为
(3)
4.2. 拟合趋势效应
用函数
(4)
对序列中的趋势效应进行提取。由于广东省鸡蛋价格序列线性明显,因此用一元线性的模型进行拟合。利用极大似然法可以得到趋势效应部分的模型为
(5)
所有的参数估计量都通过了检验。绘制出趋势线的效果图如图4。

Figure 4. The trend effect is fitted with the power function of time t as the independent variable
图4. 以时间t的幂函数为自变量的趋势效应拟合效果图
4.3. 拟合残差序列
先对残差序列进行自相关检验。通过检验得出残差序列高度正相关,因此残差序列中还有信息没有被完全提取出来,仍需要继续分析。在前面分析的基础上,对残差自回归的模型参数进行估计,将所有的参数联合求解,同时进行参数分析,逐步剔除不显著的参数。根据结果显示,以时间的幂函数为自变量的确定性趋势模型残差序列为:
(6)
4.4. 残差自回归模型的确定
根据上述结果,可以得到拟合广东省2003年至2011年鸡蛋价格发展的残差自回归模型为:
(7)
该模型对应的AIC值为43.8154943,SBC值为51.861888。对该模型的残差序列进行自相关检验,得到各阶的DW都接近2,即残差序列不存在自相关的情况,满足要求。
4.5. 残差自回归模型预测
根据所建立的残差自回归模型对广东省2012年1月~12月的鸡蛋价格做出预测,预测结果如表6。将结果绘制出效果图如图5,其中黑点为真实观察值,红线为估计和预测值,绿线为估计值的上下限。根据效果图可以看出该模型拟合效果较好,基本所有的鸡蛋价格都落在置信区间内。

Figure 5. Auto-regressive model fitting and prediction renderings
图5. 残差自回归模型拟合和预测效果图

Table 6. Prediction of egg price in Guangdong Province from January to December 2012 by auto-regressive model (unit: Yuan)
表6. 残差自回归模型广东省2012年1月~12月鸡蛋价格预测(单位:元)
5. 模型对比
本节将从模型的理论层面、拟合统计量以及预测效果两个方面对这两个模型进行对比评价,最终选出最适合预测广东省鸡蛋价格的模型。
5.1. 模型理论层面
乘积季节ARIMA模型在本文构建过程中,对差分后的序列进行了深入分析,充分考虑了季节效应、长期趋势效应和随机波动的相互关系。这种综合考虑使得模型能够更好地捕捉广东省鸡蛋价格序列数据的内在规律,从而使信息充分提取,提高了预测的准确性。该模型结构也相对比较简单,易于理解和实现,在短期预测方面突出。然而,该模型用差分提取确定性信息,使得确定因素不明显,模型不直观,导致解释性较差。
残差自回归模型的构建思想与ARIMA模型大致相同。在模型构建的起始阶段,同样首先对广东省鸡蛋原始价格序列数据进行确定性信息的提取,如季节效应、长期趋势等。接着对提取后的确定性信息所形成的残差序列进行自回归模型的拟合。这一步骤使得模型能够更好地捕捉残差中剩余有用的信息,包括自相关性和非线性关系。残差自回归模型将所有参数进行联合求解,从而在求解过程中自动进行参数检验,逐步剔除不显著的参数,提高模型的解释性和预测能力。残差自回归模型的一个显著优点是得出的模型具有明确的确定因素,模型结构相对直观,易于解释原序列的规律。然而残差自回归模型对原始序列的总体规律分析使得它更适合长期预期,而不适合作为短期的精确预测。
综上,ARIMA模型和残差自回归模型各有优点和缺点。二者都考虑到广东省鸡蛋价格数据本身的季节效应、长期趋势和随机波动,都有较好的信息提取和预测能力;ARIMA模型预测较为准确,在短期预测方面突出,但解释性较差,残差自回归模型结构直观,易于理解,但更适合长期预测。因此在预测鸡蛋价格时需要根据实际预测需求进行选择。
5.2. 评价指标对比
模型拟合完成后,利用2003年1月至2011年12月鸡蛋价格样本数据的真实值与两种模型的拟合值,计算两种模型拟合优劣程度的评价指标值,通过比较指标大小评价两个模型拟合的优劣程度。计算ARIMA模型与残差自回归模型拟合结果的评价指标值如表7。

Table 7. Comparison of evaluation index values of two models
表7. 两个模型评价指标值对比
通过对比两个模型的评价指标值,可以发现ARIMA模型的R方,均方误差MAE、飓风根误差RMSE、平均绝对误差MAE、平均绝对误差比MAPE以及AIC和SBC信息准则都小于残差自回归的指标值,所以综合来看,虽然ARIMA模型R方略低于残差自回归模型,但还是认为乘积季节模型
的拟合效果更优。
5.3. 预测效果对比
由于广东省各月份鸡蛋价格只更新到2011年12月,因此以已公布的2012年鸡蛋平均价格为标准,对两个模型的预测结果做对比。已知2012年广东省鸡蛋平均价格为11.26元/公斤,而ARIMA模型预测出来的2012年广东省鸡蛋平均价格为11.53234元/公斤,残差自回归模型预测出来的2012年广东省鸡蛋平均价格为11.5873元/公斤。可以看出ARIMA模型预测出来的平均价格更加接近真实情况。
6. 结论
综上所述,认为应该选择
模型预测广东省鸡蛋价格。该模型预测2012年1月至2013年12月的鸡蛋价格如表8及预测图如图6。

Table 8. ARIMA model forecast of egg price in Guangdong Province from 2012 to 2013 (unit: Yuan)
表8. ARIMA模型广东省2012年~2013年鸡蛋价格预测(单位:元)

Figure 6. ARIMA model fitting and prediction renderings
图6. ARIMA模型拟合和预测效果图
根据构建的
模型,可以看出鸡蛋总体价格呈现长期线性增长趋势,同时具有以12月为周期的季节性特征。除了长期增长趋势和季节性之外,鸡蛋价格在某月还会受到八个月前的随机误差项的正向影响,以及上一年同一月份的随机误差项的负向影响。同时根据模型还可以得知,鸡蛋价格仅受一年内的价格波动影响,两年及以前的价格变动对当前鸡蛋价格的影响较小。这些发现对于预测和制定相关政策具有重要意义,同时该模型有助于根据已有的鸡蛋价格预测未来的鸡蛋价格,从而更好地理解鸡蛋市场的运行规律。
接着对预测结果进行分析,以深入探究价格变动原因,从而加以证明了应用ARIMA模型预测的优势。在乘积季节ARIMA模型的预测下,广东省2012年和2013年的鸡蛋价格并没有呈现过大的波动和明显的增长趋势,但是揭示了鸡蛋价格在某些月份的季节性波动。具体来说,2012年的最低零售价格出现在5月份,为每公斤11.16元,4、5、6、7月份的鸡蛋价格都较低,呈现低迷状态。之后,鸡蛋价格开始上升,并在9月份达到最高点,预测价格为每公斤11.81元。这一预测结果与前一年的鸡蛋价格实际运行情况基本相符。对于2013年的鸡蛋价格预测,也呈现出了类似的规律。最低蛋价为5月份的11.55元,最高蛋价为9月份的12.42元。这些现象都可以被解释:4、5月份为春节过后的月份,市场消费需求减弱,同时春季气候变暖使得蛋鸡产蛋率提升,导致鸡蛋供给增加,两者共同作用使鸡蛋价格回落。而9月份由于中秋、国庆佳节和学校开学等节假日因素,鸡蛋市场需求量激增,助推蛋价高位运行。总的来说,乘积季节ARIMA模型预测的2012年和2013年广东省鸡蛋价格呈现了一定的季节性波动,符合市场实际运行情况,模型表现情况较为优秀。这为相关企业和消费者提供了有价值的参考信息,有助于更好地理解和预测未来鸡蛋市场的价格走势。
基于上述广东省鸡蛋价格的季节性波动特点,政府部门、养殖户、投资者和消费者都需要采取相应的措施。政府部门应不断加强对鸡蛋价格的监测预警,全面掌握鸡蛋价格的运行规律,并及时向社会公布相关价格数据信息。一旦发现倾向性、苗头性的问题,政府部门应迅速干预鸡蛋市场,以维护市场稳定。对于养殖户而言,他们需要根据鸡蛋价格的季节性特点合理安排生产计划,例如4、5月份鸡蛋价格较低而9月份鸡蛋价格较高,要避免盲目补栏或淘汰蛋鸡。对于投资者,要了解鸡蛋市场的季节性和趋势性变化,合理配置投资组合,降低投资风险,同时要注意到鸡蛋价格的随机性,及时调整投资策略,提高投资收益。对于消费者来说,他们需要在合理搭配营养的基础上,理性消费鸡蛋。避免盲目跟风,在鸡蛋价格较低时疯抢鸡蛋,要确保自己的消费选择是基于实际需求和营养需求。
综上所述,为了促进鸡蛋市场的健康稳定发展,政府部门、养殖者、投资者和消费者都需要正确看待鸡蛋市场,采取相应的措施,共同维护鸡蛋市场的稳定和繁荣。
附录